- Главная
- Математика
- Вычисление неопределенного интеграла

Содержание
Слайд 2.
∫cos(x2–3)xdx;
y = cos(x2–3) – сложная функция;
(x2 – 3x) – ее “внутренняя”
.
∫cos(x2–3)xdx;
y = cos(x2–3) – сложная функция;
(x2 – 3x) – ее “внутренняя”

часть.
Сделаем замену: t= x2 – 3x.
Как видим, переменная интегрирования не совпадает с переменной, стоящей под знаком дифференциала: cos t·x·dx .
Поэтому найдем дифференциал от t, и заменим dx на dt. Результат замены оформим следующим образом:
Если подставить в интеграл новую функцию, то получим
Вычислить интеграл:
- Предыдущая
Исследовательский подходСледующая -
Откуда хлеб на столе? Прямоугольник. Квадрат. Периметр многоугольника
Прямоугольник. Квадрат. Периметр многоугольника Таблица умножения. Урок математики. 3 класс
Таблица умножения. Урок математики. 3 класс Линейная алгебра
Линейная алгебра 6a04a5dd-75c3-461b-a240-737df2a5d137
6a04a5dd-75c3-461b-a240-737df2a5d137 Множество значений тригонометрических функций
Множество значений тригонометрических функций Организация исследовательской деятельности учащихся на уроках математики
Организация исследовательской деятельности учащихся на уроках математики Процент
Процент Выполнение плана чертежа в масштабе
Выполнение плана чертежа в масштабе Свойство углов треугольника
Свойство углов треугольника Это полезно знать. Математика в кулинарии
Это полезно знать. Математика в кулинарии Свидание. Личный сайт
Свидание. Личный сайт Презентация на тему Порядок выполнения действий в выражениях со скобками
Презентация на тему Порядок выполнения действий в выражениях со скобками  Построение угла, равного данному
Построение угла, равного данному Морское путешествие
Морское путешествие Арифметический квадратный корень. Задания для устного счета. 8 класс
Арифметический квадратный корень. Задания для устного счета. 8 класс Актуализация знаний
Актуализация знаний Применение теоремы Пифагора
Применение теоремы Пифагора Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка
Лекция. Матрицы.Операции над матрицами.Определители матриц 2 и 3 порядка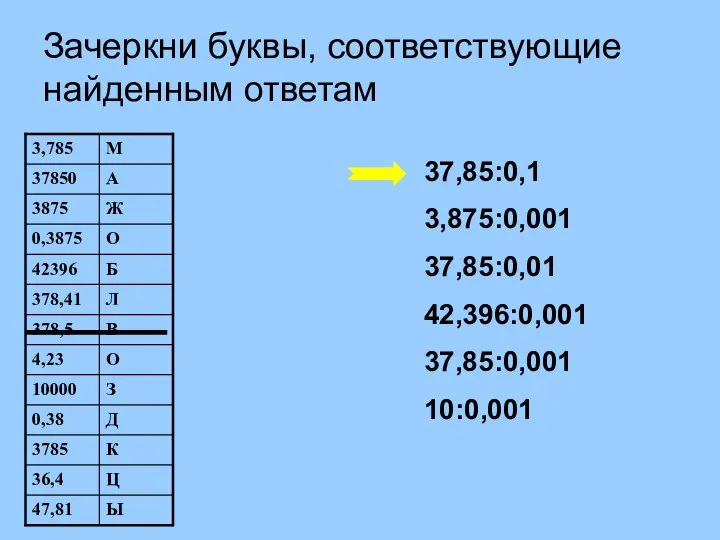 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Решение задач по теме Равнобедренный треугольник
Решение задач по теме Равнобедренный треугольник Выборка. Обобщение введенных понятий
Выборка. Обобщение введенных понятий Математика вокруг нас. Геометрия на столе с ножницами и без
Математика вокруг нас. Геометрия на столе с ножницами и без Знаки неравенств. Историческая справка
Знаки неравенств. Историческая справка Школа олимпийского резерва. (задача)
Школа олимпийского резерва. (задача) Аксиомы стереометрии
Аксиомы стереометрии Математическая статистика
Математическая статистика Решение задач
Решение задач Презентация на тему Дифференциальные уравнения первого порядка
Презентация на тему Дифференциальные уравнения первого порядка