Системы линейных уравнений

Системы линейных уравнений
Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
Система m линейных уравнений с n переменными:

Числа
называются коэффициентами при переменных, а
свободными членами.
Совокупность чисел
называется решением системы линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

В школьном курсе рассматриваются способ подстановки и
способ сложения.
В курсе высшей математике решают методом Крамера ,методом Гаусса и с помощью обратной матрицы.
Рассмотрим решение систем линейных уравнений методом Крамера

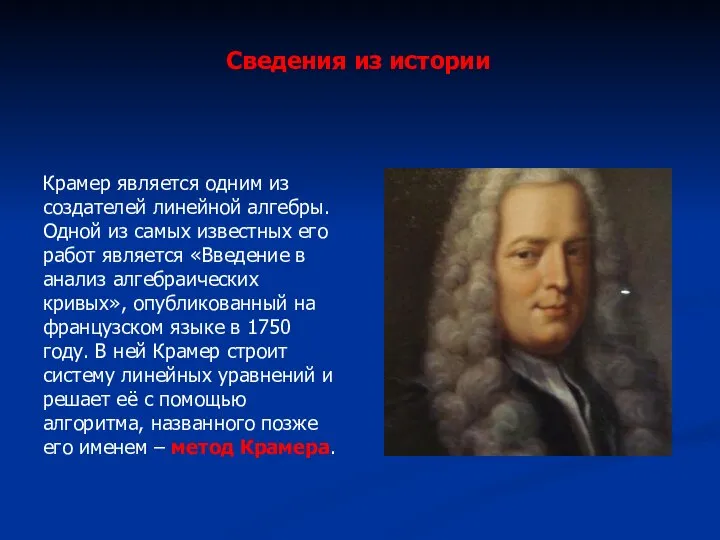
Сведения из истории
Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.

Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача. Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.
В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Юноша так понравился магистрату, что специально для него и ещё одного одного кандидата на место преподавателя была учреждена отдельная кафедра математики, где Крамер и работал в последующие годы.

Учёный много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне, Мопертюи и Клеро в Париже и других. Со многими из них он продолжал переписываться всю жизнь.
В 1729 году Крамер возобновляет преподавательскую работу в Женевском университете. В это время он участвует в конкурсе Парижской Академии и занимает второе место.
Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике.
В 1740-е гг. Иоганн Бернулли поручает Крамеру подготовить к печати сборник своих работ. В 1742 году Крамер публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира. Габриэль Крамер скончался 4 января 1752 года во Франции

Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Решение системы линейных уравнений методом Крамера

Дана система

Составим главный определитель системы:

Заменяя столбец с коэффициентами соответствующей переменной свободными членами:

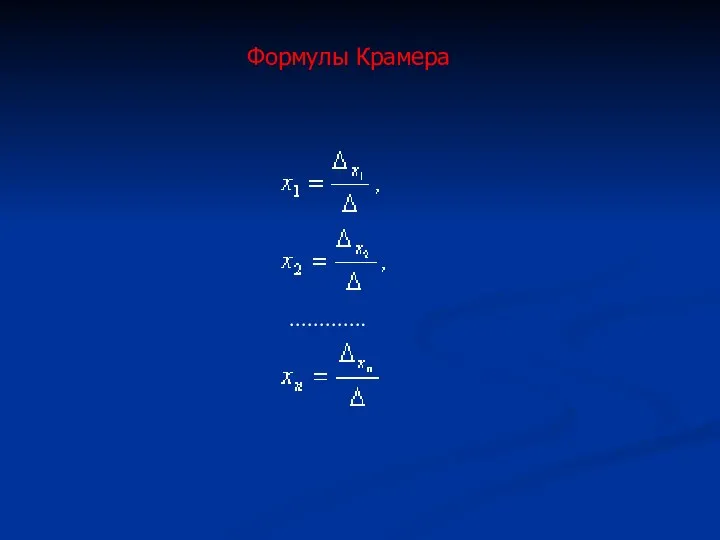
Формулы Крамера
………….

1) система линейных уравнений имеет единственное решение
(система совместна и определённа)
Условия:
При решении системы уравнений могут встретиться три случая:

2) система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
Условия:
т.е. коэффициенты при неизвестных и свободные члены пропорциональны

3) система линейных уравнений решений не имеет
(система несовместна)
Условия:
Система называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Решение системы трех линейных уравнений с
тремя двумя неизвестными методом Крамера
Решение. Находим определители системы:

Ответ: (1; 0; -1) .