Содержание
- 2. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности — каждое из значений Xi является суммой
- 3. Вероятностное описание результатов и погрешностей Разброс результатов измерений – диапазон измеренной ФВ от минимального до максимального
- 4. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Пусть произведено n последовательных наблюдений одной и
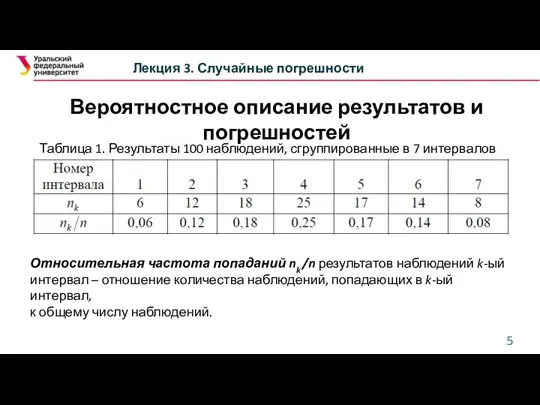
- 5. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Таблица 1. Результаты 100 наблюдений, сгруппированные в
- 6. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности На основании полученных результатов можно построить гистограмму
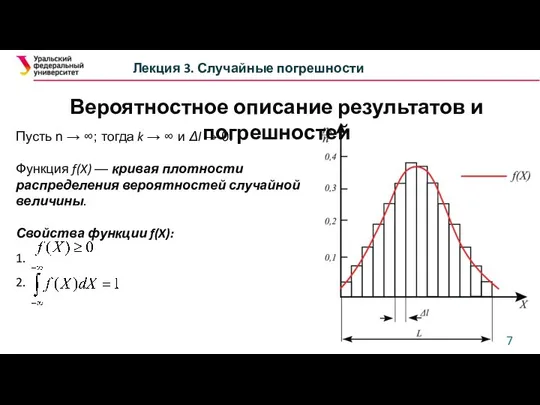
- 7. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Пусть n → ∞; тогда k →
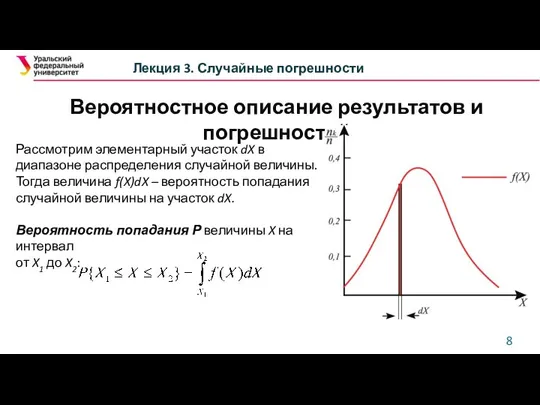
- 8. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Рассмотрим элементарный участок dX в диапазоне распределения
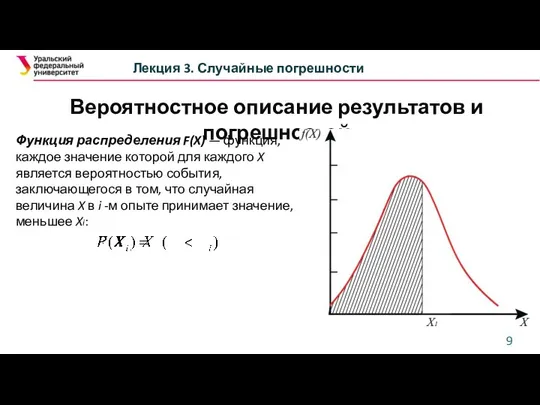
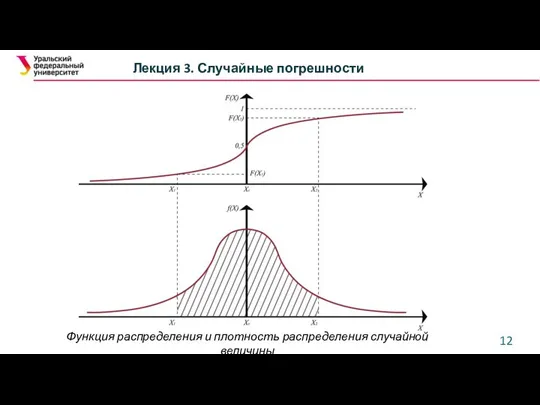
- 9. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Функция распределения F(X) — функция, каждое значение
- 10. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Перепишем выражение для функции распределения F(X): Тогда
- 11. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Свойства функции F(X): 1. F(X1) ≥0; 2.
- 12. Лекция 3. Случайные погрешности Функция распределения и плотность распределения случайной величины
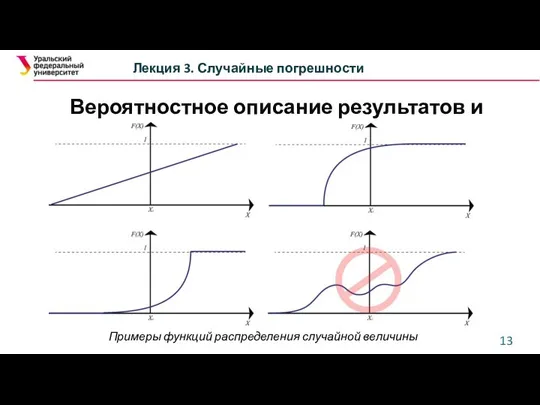
- 13. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Примеры функций распределения случайной величины
- 14. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Кумулятивная кривая – график дискретной функции распределения.
- 15. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Функция распределения числа очков при бросании игральной
- 16. Вероятностное описание результатов и погрешностей Лекция 3. Случайные погрешности Размерности функции распределения и плотности распределения —
- 17. Лекция 3. Случайные погрешности Примеры заданий 1. Задают ли следующие таблицы законы распределения дискретной случайной величины?
- 18. Лекция 3. Случайные погрешности Примеры заданий 1. Задают ли следующие таблицы законы распределения дискретной случайной величины?
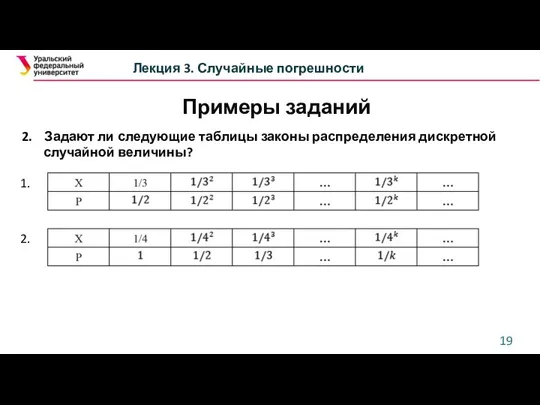
- 19. Лекция 3. Случайные погрешности Примеры заданий 2. Задают ли следующие таблицы законы распределения дискретной случайной величины?
- 20. Лекция 3. Случайные погрешности Примеры заданий 2. Задают ли следующие таблицы законы распределения дискретной случайной величины?
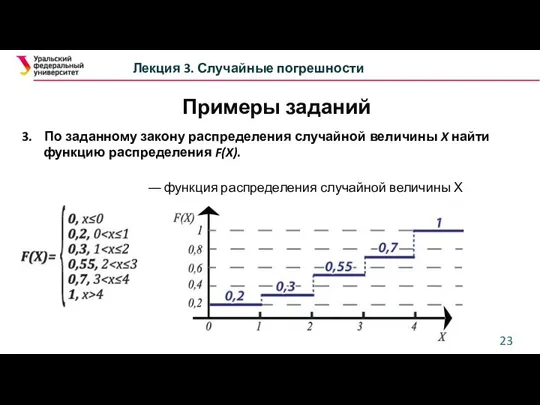
- 21. Лекция 3. Случайные погрешности Примеры заданий 3. По заданному закону распределения случайной величины X найти функцию
- 22. Лекция 3. Случайные погрешности Примеры заданий 3. По заданному закону распределения случайной величины X найти функцию
- 23. Лекция 3. Случайные погрешности Примеры заданий 3. По заданному закону распределения случайной величины X найти функцию
- 24. Лекция 3. Случайные погрешности Примеры заданий 4. Плотность распределения случайной величины задана формулой: Найти вероятность того,
- 25. Лекция 3. Случайные погрешности Примеры заданий 4. Плотность распределения случайной величины задана формулой: С помощью выражения
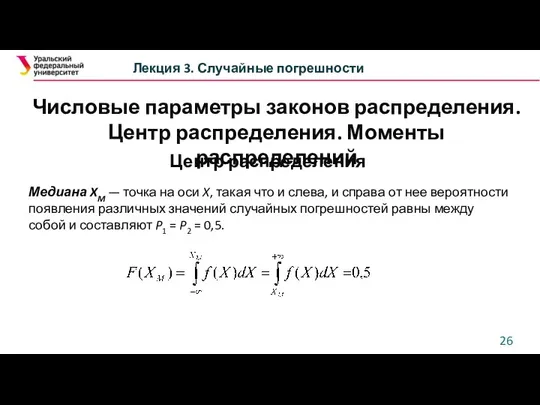
- 26. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Центр распределения Медиана XM
- 27. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Центр распределения Мода Xm
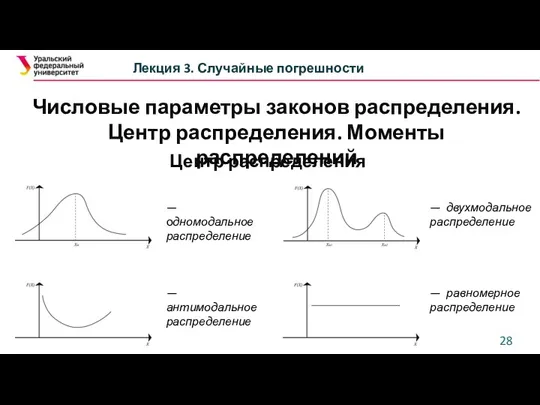
- 28. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Центр распределения — одномодальное
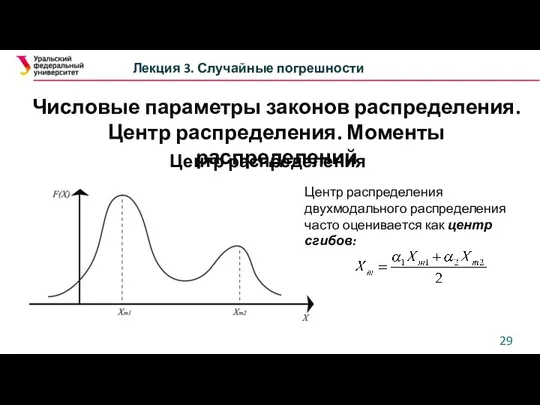
- 29. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Центр распределения Центр распределения
- 30. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Центр распределения Математическое ожидание
- 31. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Центр распределения Центр размаха
- 32. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Моменты распределений Начальные моменты
- 33. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Моменты распределений Центральные моменты
- 34. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Моменты распределений Дисперсия —
- 35. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Моменты распределений Третий центральный
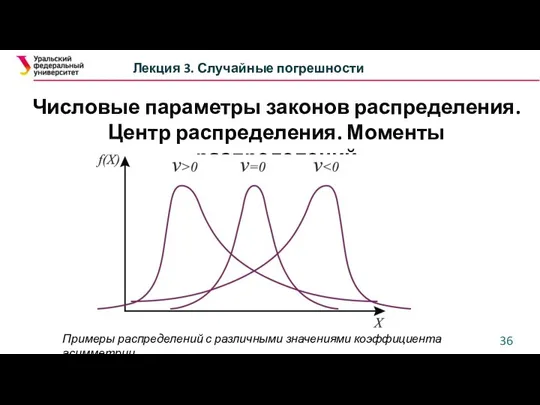
- 36. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Примеры распределений с различными
- 37. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Моменты распределений Четвертый центральный
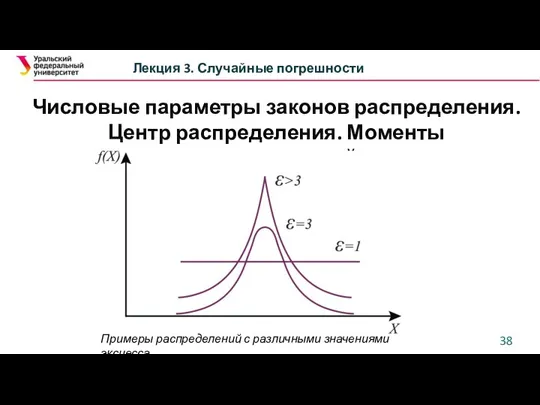
- 38. Числовые параметры законов распределения. Центр распределения. Моменты распределений Лекция 3. Случайные погрешности Примеры распределений с различными
- 39. Распределения случайных величин Лекция 3. Случайные погрешности Формы кривых распределения случайных величин Трапецеидальные Экспоненциальные Семейство распределений
- 40. Лекция 3. Случайные погрешности Трапецеидальные распределения 1. Равномерное распределение Распределения случайных величин
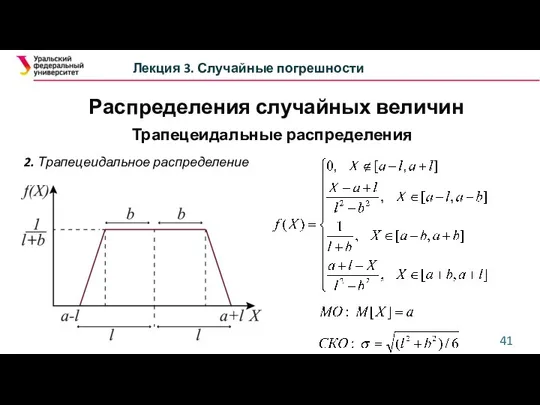
- 41. Лекция 3. Случайные погрешности Трапецеидальные распределения 2. Трапецеидальное распределение Распределения случайных величин
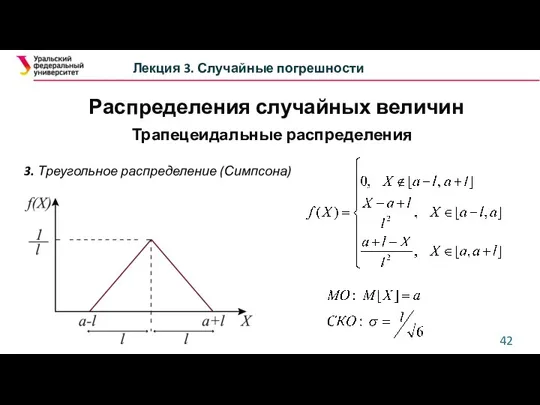
- 42. Лекция 3. Случайные погрешности Трапецеидальные распределения 3. Треугольное распределение (Симпсона) Распределения случайных величин
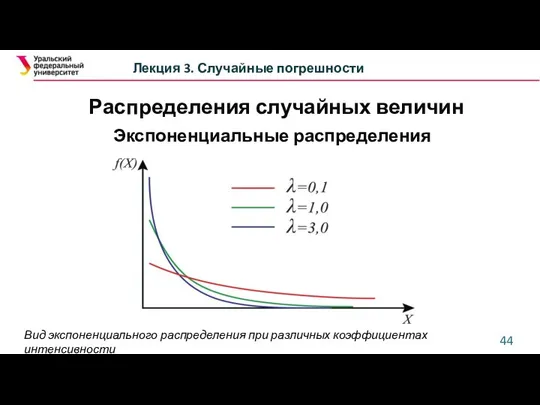
- 43. Лекция 3. Случайные погрешности Экспоненциальные распределения 1. Экспоненциальное распределение λ >0 — коэффициент интенсивности или обратный
- 44. Лекция 3. Случайные погрешности Экспоненциальные распределения Вид экспоненциального распределения при различных коэффициентах интенсивности Распределения случайных величин
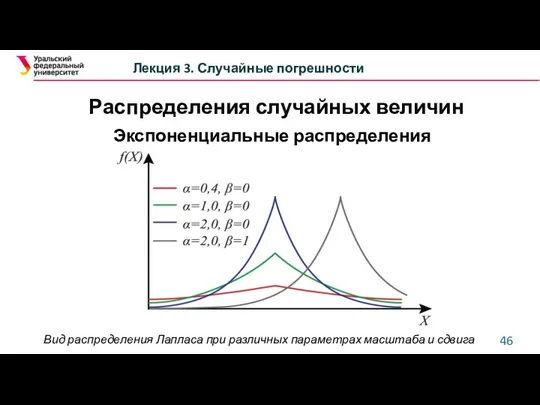
- 45. Лекция 3. Случайные погрешности Экспоненциальные распределения 2. Распределение Лапласа α >0 — параметр масштаба, -∞ —
- 46. Лекция 3. Случайные погрешности Экспоненциальные распределения Вид распределения Лапласа при различных параметрах масштаба и сдвига Распределения
- 47. Лекция 3. Случайные погрешности Экспоненциальные распределения 3. Нормальное распределение (Гаусса) — плотность распределения Величина µ —
- 48. Лекция 3. Случайные погрешности Экспоненциальные распределения 3. Нормальное распределение (Гаусса) — функция распределения — функция ошибок
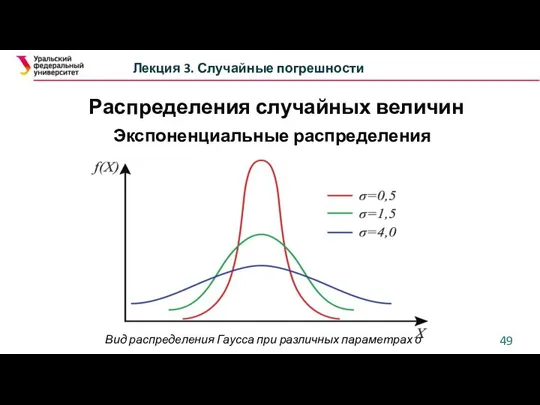
- 49. Лекция 3. Случайные погрешности Экспоненциальные распределения Вид распределения Гаусса при различных параметрах σ Распределения случайных величин
- 50. Лекция 3. Случайные погрешности Семейство распределений Стьюдента 1. Распределение Стьюдента (t-распределение) Пусть ξ0, ξ1 … ξm
- 51. Лекция 3. Случайные погрешности Семейство распределений Стьюдента 1. Распределение Стьюдента (t-распределение) Тогда плотность распределения случайной величины
- 52. Лекция 3. Случайные погрешности Семейство распределений Стьюдента Свойства распределения Стьюдента При m>1 математическое ожидание = медиана
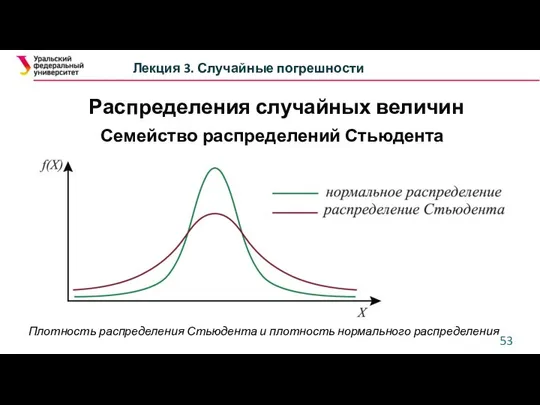
- 53. Лекция 3. Случайные погрешности Семейство распределений Стьюдента Плотность распределения Стьюдента и плотность нормального распределения Распределения случайных
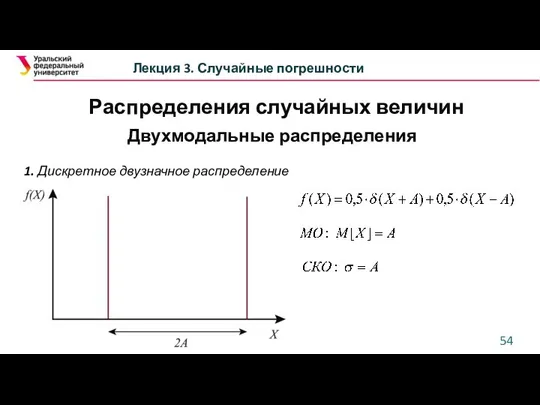
- 54. Лекция 3. Случайные погрешности Двухмодальные распределения 1. Дискретное двузначное распределение Распределения случайных величин
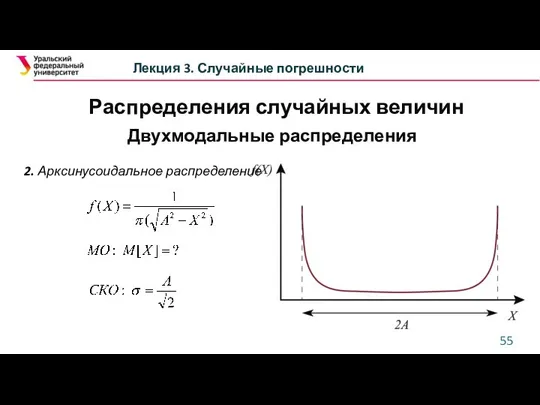
- 55. Лекция 3. Случайные погрешности Двухмодальные распределения 2. Арксинусоидальное распределение Распределения случайных величин
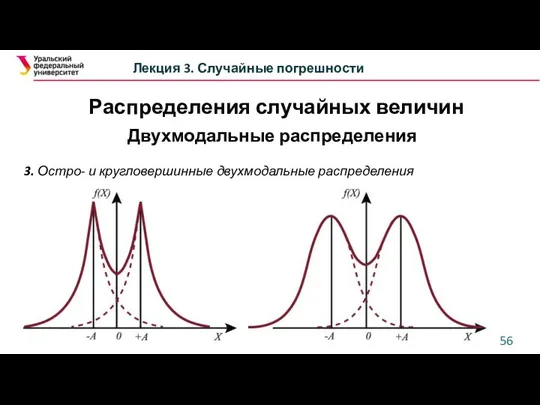
- 56. Лекция 3. Случайные погрешности Двухмодальные распределения 3. Остро- и кругловершинные двухмодальные распределения Распределения случайных величин
- 57. Оценка результата измерения Лекция 3. Случайные погрешности Точечная оценка параметра — оценка параметра, выраженная одним числом.
- 58. Оценка результата измерения Лекция 3. Случайные погрешности Точечной оценкой математического ожидания результата измерений является среднее арифметическое
- 59. Оценка результата измерения Лекция 3. Случайные погрешности Точечная оценка среднего квадратического отклонения определяется по формуле: Среднее
- 60. Лекция 3. Случайные погрешности — нормальное распределение Введем величину погрешности — кривая нормального распределения случайных погрешностей
- 61. Лекция 3. Случайные погрешности Свойства распределения случайных погрешностей Кривая нормального распределения погрешностей симметрична относительно оси ординат;
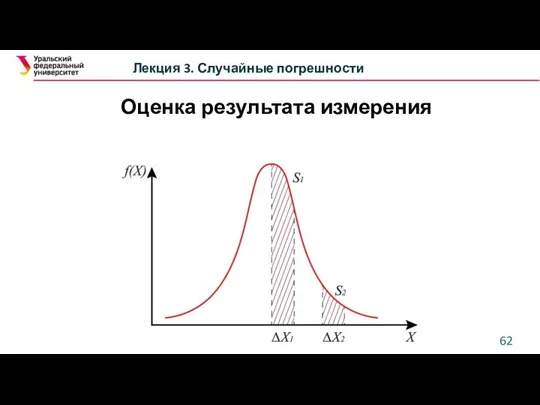
- 62. Лекция 3. Случайные погрешности Оценка результата измерения
- 63. Лекция 3. Случайные погрешности Введем нормированную случайную величину: — плотность распределения — функция распределения Оценка результата
- 64. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Квантильные оценки — интервал
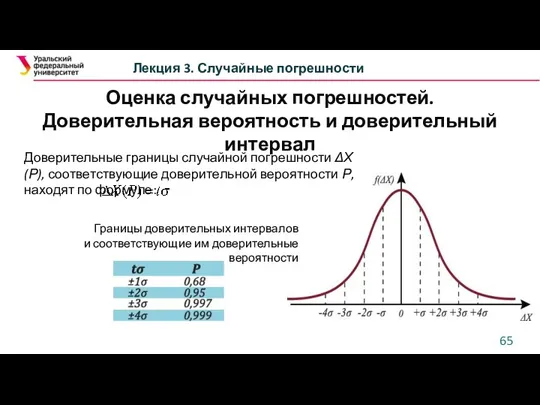
- 65. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Доверительные границы случайной погрешности
- 66. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Для получения интервальной оценки
- 67. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности 3. Найти верхнюю и
- 68. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Для определения численного значения
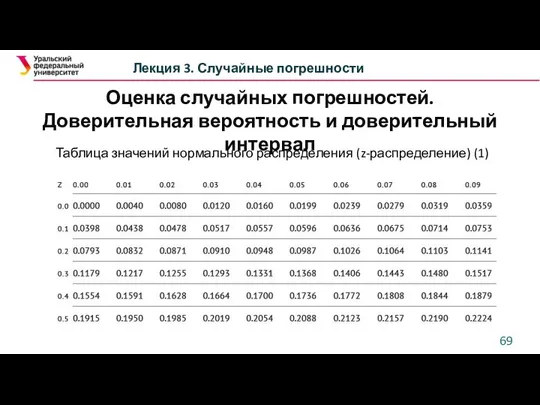
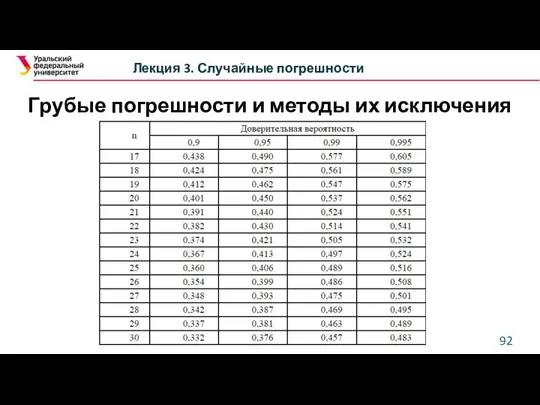
- 69. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
- 70. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
- 71. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
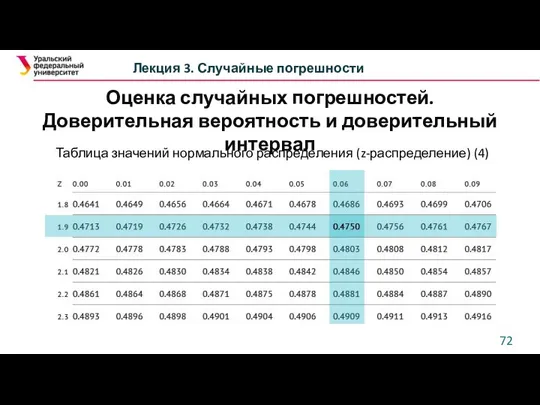
- 72. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
- 73. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
- 74. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
- 75. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений нормального распределения
- 76. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности 1. Определить среднее значение
- 77. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Для нормального распределение при
- 78. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Вероятность того, что дробь
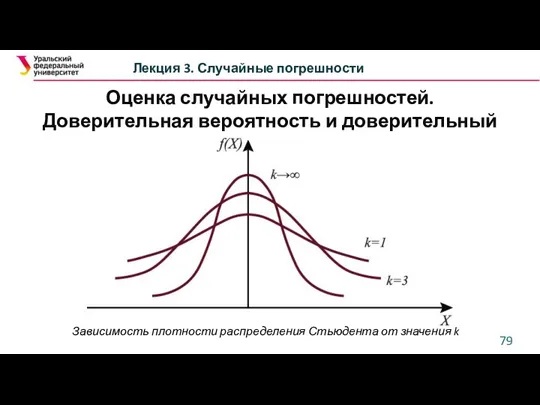
- 79. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Зависимость плотности распределения Стьюдента
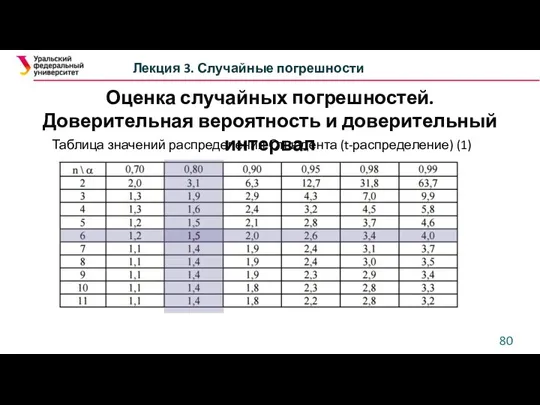
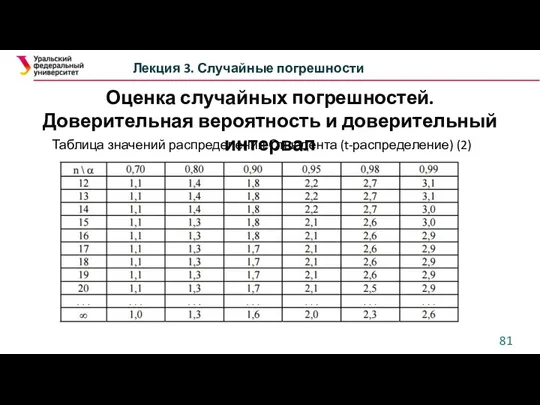
- 80. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений распределения Стьюдента
- 81. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности Таблица значений распределения Стьюдента
- 82. Оценка случайных погрешностей. Доверительная вероятность и доверительный интервал Лекция 3. Случайные погрешности 2. Даны следующие значения
- 83. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Грубая погрешность, или промах – результат
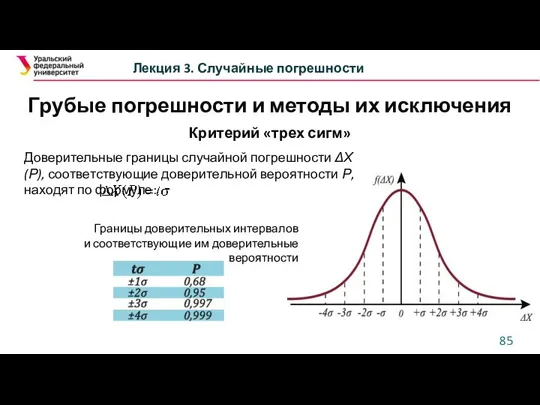
- 84. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Критерий «трех сигм» Результат, возникающий с
- 85. Лекция 3. Случайные погрешности Доверительные границы случайной погрешности ΔХ(Р), соответствующие доверительной вероятности Р, находят по формуле:
- 86. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Критерий «трех сигм» 1. Даны следующие
- 87. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Критерий «трех сигм» — Величина границы
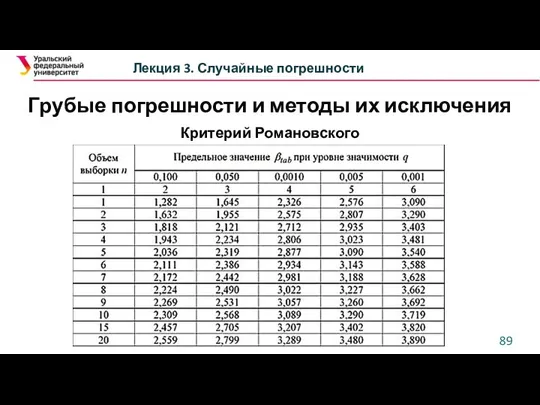
- 88. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Критерий Романовского Отбрасываются подозрительные результаты наблюдений,
- 89. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Критерий Романовского
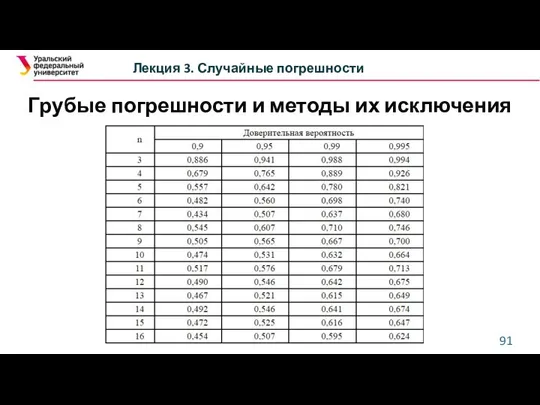
- 90. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Вариационный критерий Диксона Ряд измерений ранжируется
- 91. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Вариационный критерий Диксона
- 92. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Вариационный критерий Диксона
- 93. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Вариационный критерий Диксона 2. Даны следующие
- 94. Грубые погрешности и методы их исключения Лекция 3. Случайные погрешности Различные критерии для исключения промахов при
- 96. Скачать презентацию




























































 Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график История развития квадратных уравнений
История развития квадратных уравнений Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1) Описательная статистика
Описательная статистика Соотношения между углами и сторонами треугольника
Соотношения между углами и сторонами треугольника Решение логических задач
Решение логических задач Математика ЕГЭ. Тригонометрические выражения. Часть 1
Математика ЕГЭ. Тригонометрические выражения. Часть 1 Случаи вычитания
Случаи вычитания Метод решения систем линейных уравнений методом Крамера
Метод решения систем линейных уравнений методом Крамера Прямая призма. Решение задач
Прямая призма. Решение задач Параллельный перенос
Параллельный перенос Презентация на тему Тренажёр «Квадратные корни»
Презентация на тему Тренажёр «Квадратные корни»  Задачи. Куб, тетраэдр
Задачи. Куб, тетраэдр Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Роль геометрии в изобразительном искусстве
Роль геометрии в изобразительном искусстве Вычисление длины дуги
Вычисление длины дуги Повторение курса алгебры за 10 класс
Повторение курса алгебры за 10 класс Математика в архитектуре
Математика в архитектуре Решение треугольников
Решение треугольников Решение задач
Решение задач Не итерируемые или неизменяемые объекты
Не итерируемые или неизменяемые объекты Формулы приведения
Формулы приведения Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Поворот. Типы вращений
Поворот. Типы вращений Числові нерівності. Властивості числових нерівностей
Числові нерівності. Властивості числових нерівностей Перпендикулярные прямые
Перпендикулярные прямые Деление на 2, 3, 4, 5 (повторение)
Деление на 2, 3, 4, 5 (повторение) Средства измерений, классификация. Метрологические характеристики средств измерений
Средства измерений, классификация. Метрологические характеристики средств измерений