Слайд 2Рекомендуемая литература:
1. М.Г. Назаров. Общая теория статистики. Учебник. [Электронный ресурс] : Учебники
![Рекомендуемая литература: 1. М.Г. Назаров. Общая теория статистики. Учебник. [Электронный ресурс] :](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1142368/slide-1.jpg)
— Электрон. дан. — М. : Омега-Л, 2010. — 410 с. — Режим доступа: http://e.lanbook.com/book/5534 . Раздел «Экономика и менеджмент».
2. Годин, А.М. Статистика: Учебник. [Электронный ресурс] : Учебники — Электрон. дан. — М. : Дашков и К, 2011. — 460 с. — Режим доступа: http://e.lanbook.com/book/967 . Раздел «Экономика и менеджмент».
3.Балдин, К.В. Общая теория статистики: Учебное пособие. [Электронный ресурс] : Учебные пособия / К.В. Балдин, А.В. Рукосуев. — Электрон. дан. — М. : Дашков и К, 2010. — 312 с. — Режим доступа: http://e.lanbook.com/book/955 .Раздел «Экономика и менеджмент».
Слайд 38.3.Методика исчисления показателей, характеризующих тенденцию динамики
Задание: Определите все показатели, характеризующие тенденцию

развития данного явления во времени:
1. Абсолютные приросты базисные (накопленные) и цепные (годовые).
2. Темпы роста базисные и цепные.
3. Темпы прироста базисные и цепные.
4. Абсолютное значение одного процента прироста; темп наращивания одного процента.
5. Средний абсолютный прирост; средний темп роста; средний темп прироста.
6. Постройте график базисных и цепных темпов роста.
7. Сделайте выводы на основании расчетов.
Слайд 48.3.Методика исчисления показателей, характеризующих тенденцию динамики
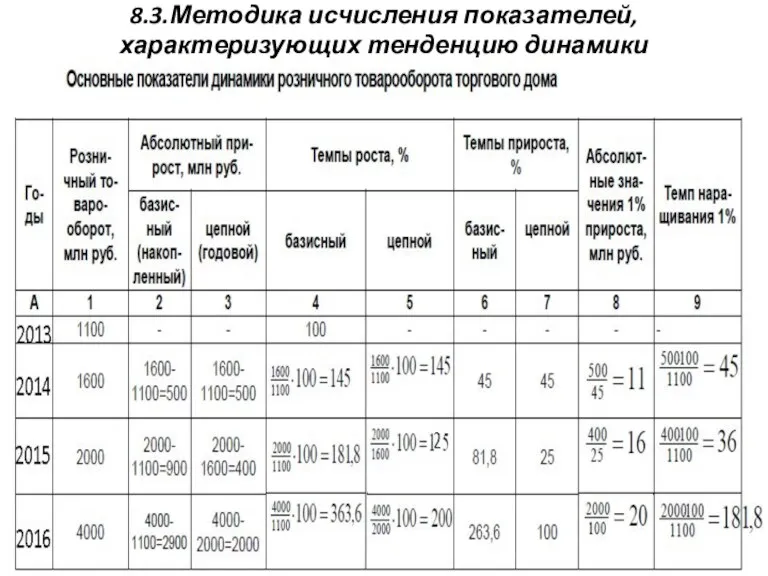
Слайд 5График динамики товарооборота торгового дома за 2013-2016 годы.
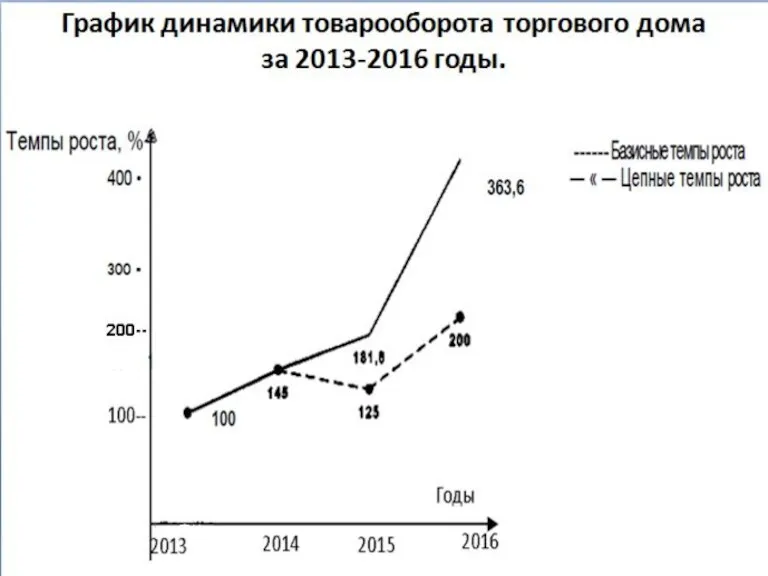
Слайд 69.ОПИСАТЕЛЬНЫЙ АНАЛИЗ: НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Графиком нормального распределения является симметричная колоколообразная кривая,

которая задается уравнением:
Слайд 79.ОПИСАТЕЛЬНЫЙ АНАЛИЗ: НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
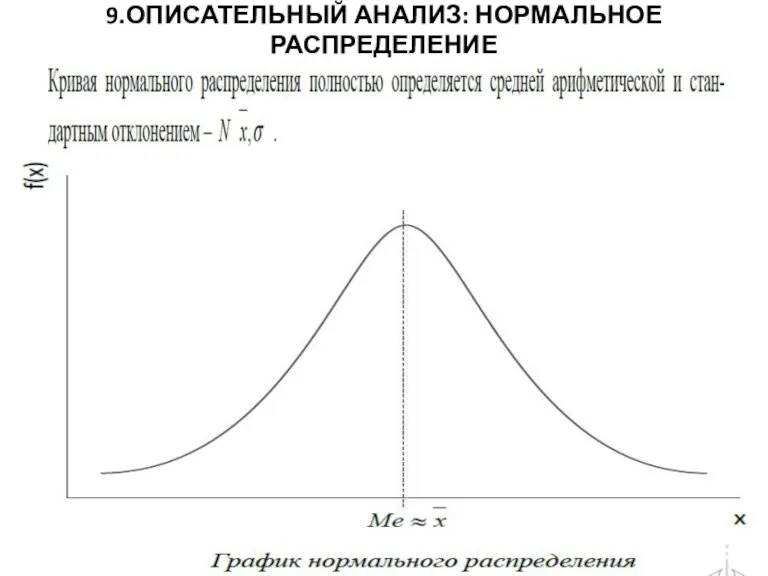
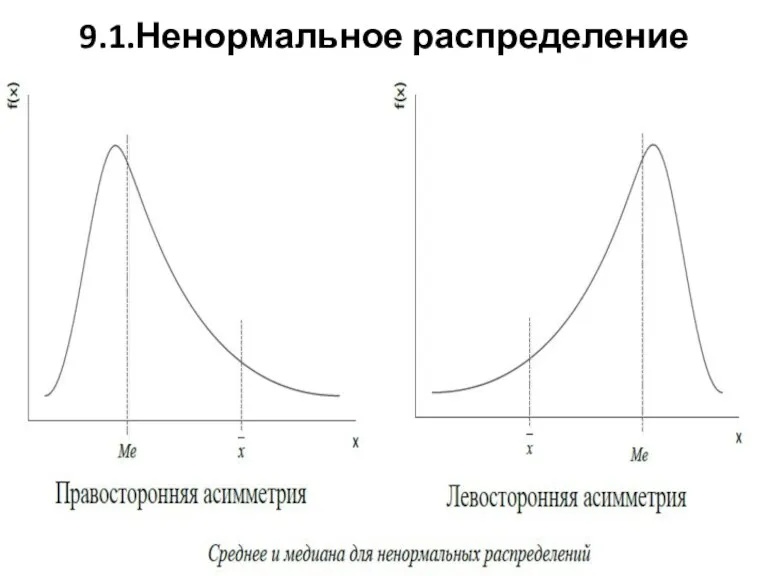
Слайд 89.1.Ненормальное распределение
Слайд 99.2.ПРОВЕРКА НА НОРМАЛЬНОСТЬ
Для проверки количественных данных на нормальность используются следующие методы:
Графические

Аналитические .
Слайд 10
9.2.1. Графические методы
9.2.1.1.Гистограмма
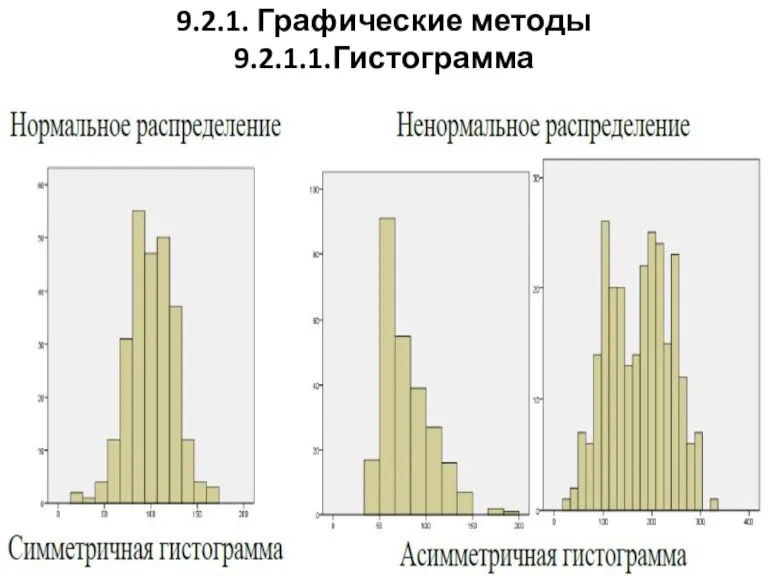
Слайд 119.2.1. Графические методы
9.2.1.1.Гистограмма
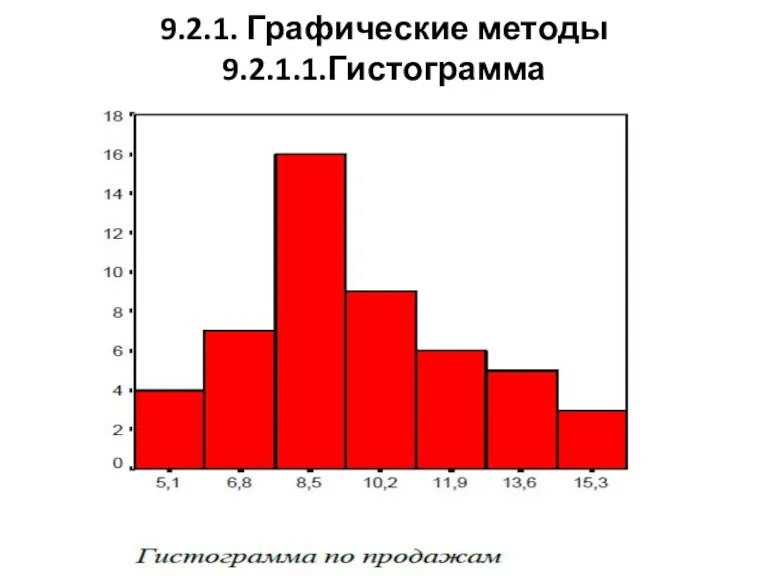
Слайд 12
9.2.1. Графические методы
9.2.1.2. «Ящик с усами»
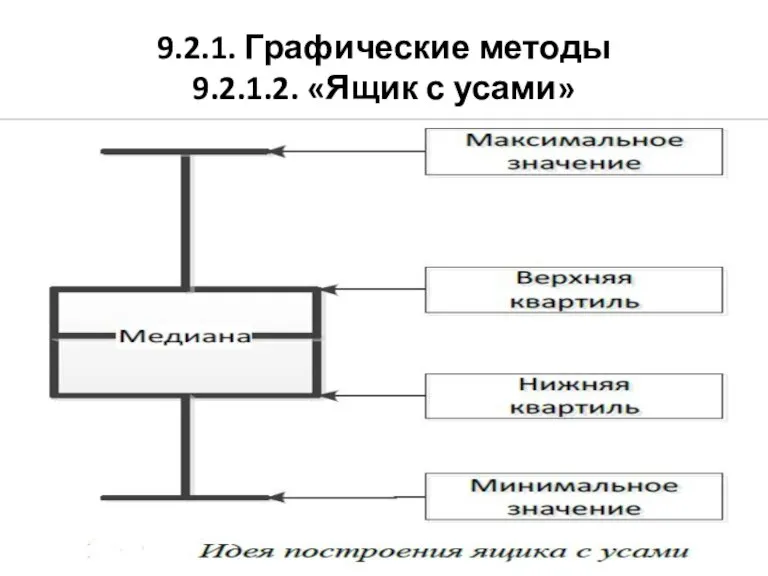
Слайд 139.2.1. Графические методы
9.2.1.2. «Ящик с усами»
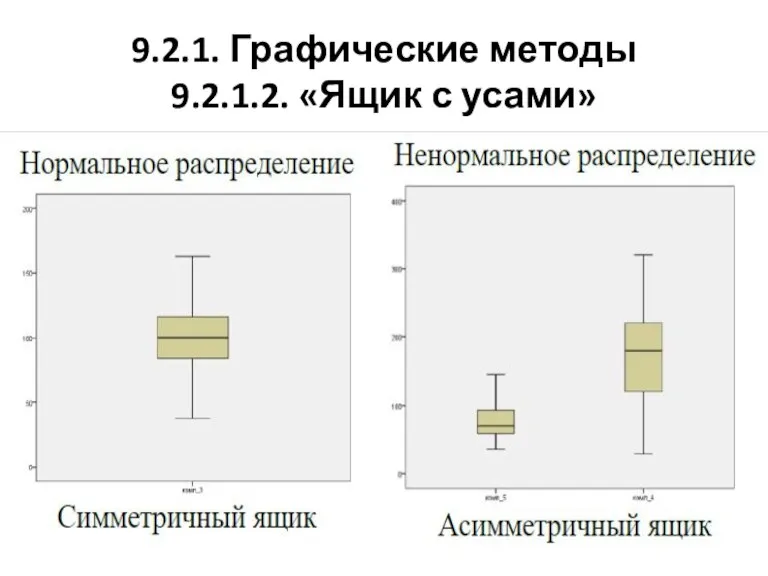
Слайд 149.2.1. Графические методы
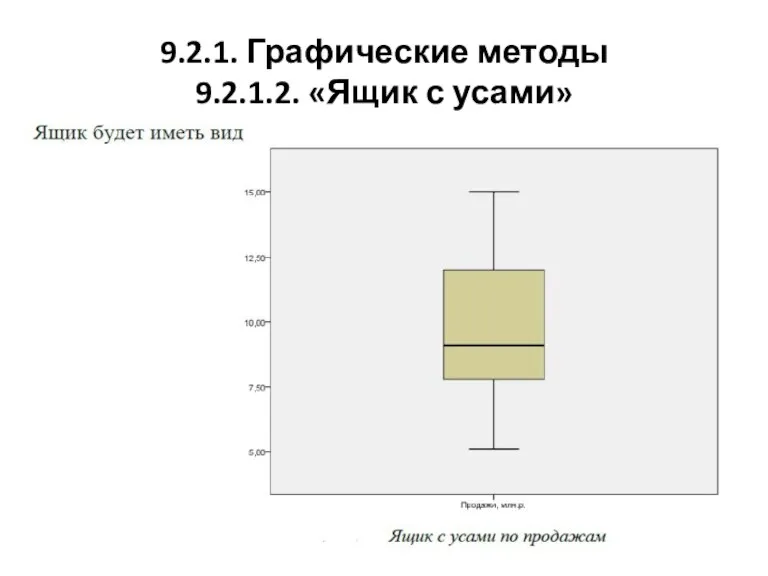
9.2.1.2. «Ящик с усами»
Построим ящик с усами по данным

Задачи 1:
Максимальное значение 15
Верхняя квартиль 11.75
Медиана 8.9
Нижняя квартиль 7.55
Минимальное значение 5.1
Слайд 159.2.1. Графические методы
9.2.1.2. «Ящик с усами»
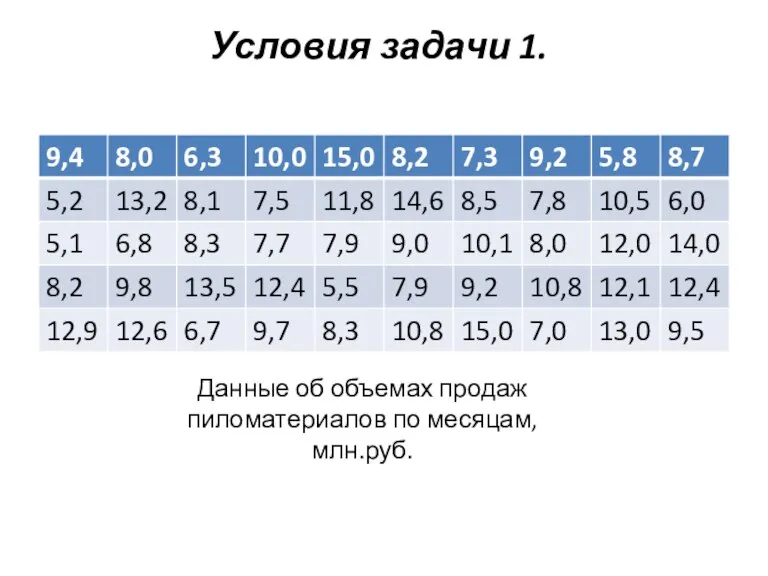
Слайд 16Условия задачи 1.
Данные об объемах продаж пиломатериалов по месяцам, млн.руб.
Слайд 17
9.2.2. Аналитические методы
Для аналитической проверки на нормальность существует различные тесты:
критерий

Хи-квадрат,
критерий Колмогорова,
критерий Шапиро-Уилка
критерий Жарка-Бера и другие.
Слайд 18
9.2.2. Аналитические методы
9.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
Суть критерия :
По данным выборки

оценивается скошенность (асимметрия) и «вытянутость» фактического распределения и сравнивается с нормальным.
Слайд 19
9.2.2. Аналитические методы
9.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
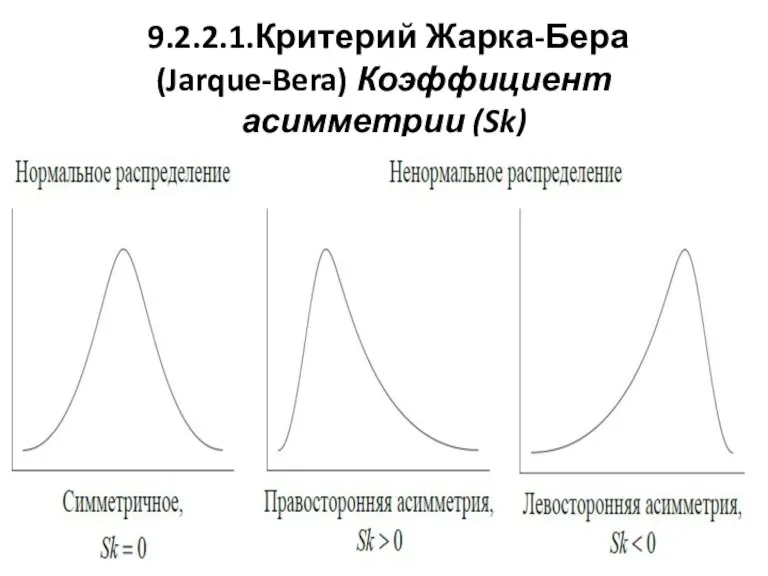
За оценку асимметрии распределения отвечает

коэффициент асимметрии (Sk):
Слайд 20
9.2.2.1.Критерий Жарка-Бера (Jarque-Bera) Коэффициент асимметрии (Sk)
Слайд 21 9.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
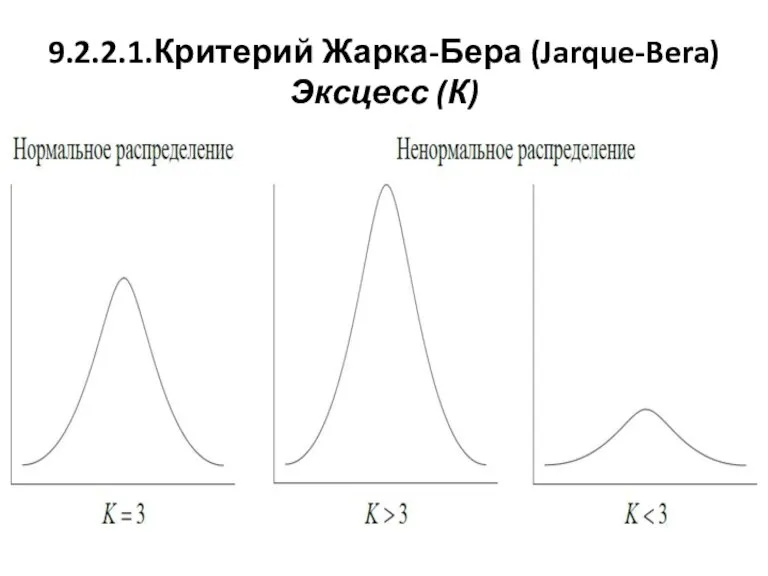
Эксцесс (К)
За оценку «вытянутости» распределения отвечает эксцесс (К):

Слайд 229.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
Эксцесс (К)
Слайд 23
9.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
Алгоритм критерия Жарка-Бера:
1) Выдвинуть гипотезу Но о нормальном

распределении выборки.
2) Вычислить фактическое значение критерия по формуле:
Слайд 249.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
Алгоритм критерия Жарка-Бера.

Слайд 259.2.2.1.Критерий Жарка-Бера (Jarque-Bera)
Алгоритм критерия Жарка-Бера.

Слайд 26
Произведем вычисления по действиям по данным предыдущего примера:
1. Составим расчетную таблицу для
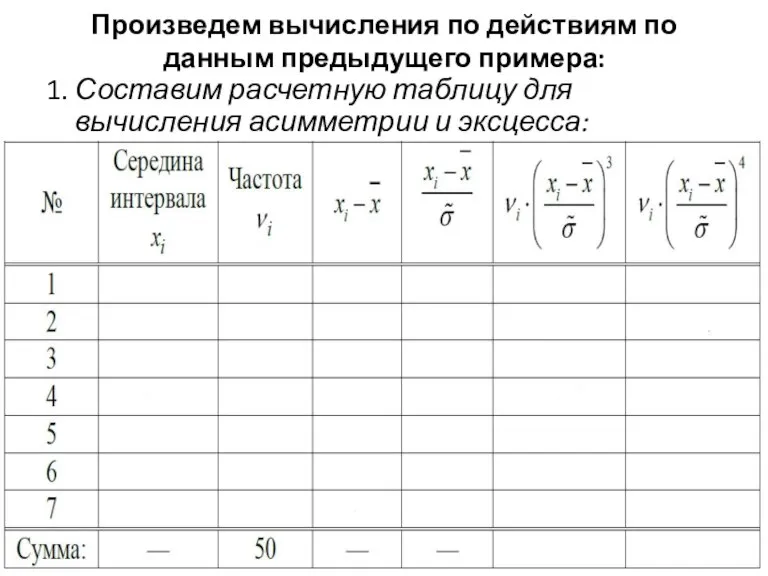
вычисления асимметрии и эксцесса:
Слайд 27
Произведем вычисления по действиям:
2. По данным расчетной таблицы произведем расчет асимметрии и

эксцесса:
Слайд 28
Произведем вычисления по действиям:
3. Выдвинем гипотезу Но о нормальном распределении выборки.
4. Вычислим

фактическое значение критерия Жарка-Бера:
Слайд 29
Произведем вычисления по действиям:
5.Произведем проверку гипотезы и сделаем выводы.

Слайд 309.3. СХЕМА ВЫБОРА АДЕКВАТНЫХ ОПИСАТЕЛЬНЫХ СТАТИСТИК
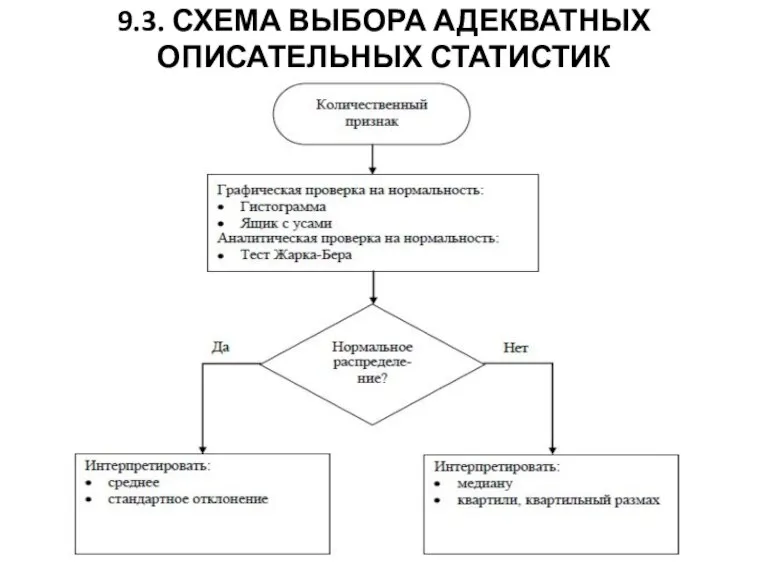
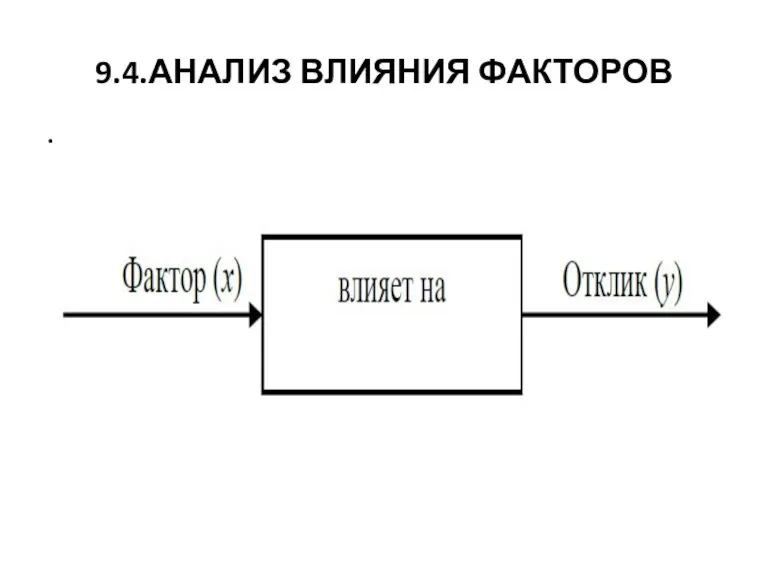
Слайд 329.4.АНАЛИЗ ВЛИЯНИЯ ФАКТОРОВ
9.4.1. Выбор метода анализа влияния факторов

Слайд 339.4.2. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Рассмотрим влияние количественного фактора на количественный отклик.
Корреляция –

мера линейной связи между двумя количественными признаками.
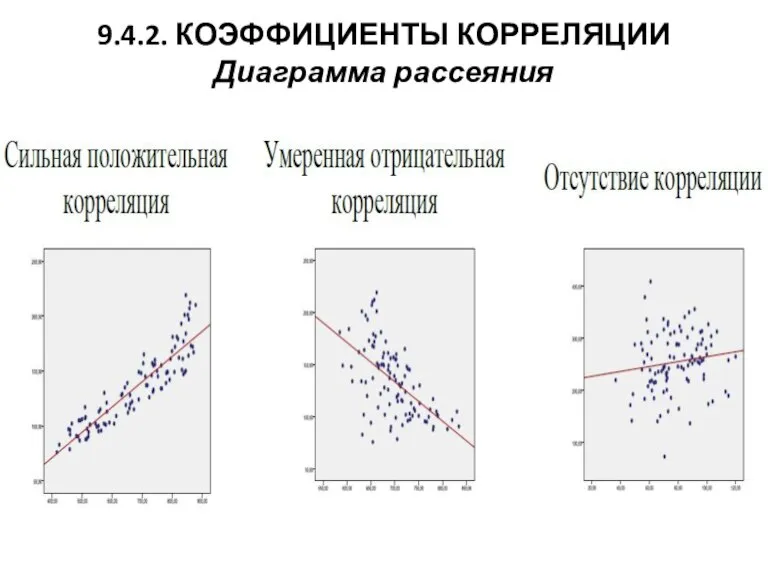
Диаграмму рассеяния – график, на котором по горизонтальной оси отмечаются значения фактора (x), а по вертикальной – отклика (y). Расположение точек говорит и о силе связи, и о ее характере.
Слайд 349.4.2. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Диаграмма рассеяния
Слайд 359.4.2. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Свойства коэффициента корреляции.
1) изменяется в пределах от -1 до

1;
2) если коэффициент корреляции менее 0,3, то значимая статистическая связь отсутствует;
3) если коэффициент корреляции равен 1 или -1, то связь не корреляционная, а функциональная (полная);
4) если коэффициент больше 0, то связь называется прямой, если меньше 0 – то обратной;
Слайд 369.4.2. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Свойства коэффициента корреляции.
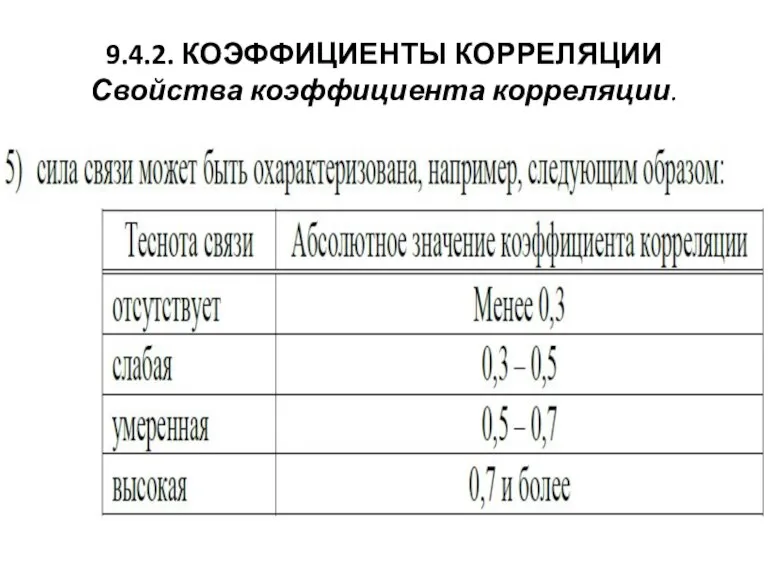
Слайд 37
9.4.2. КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
В зависимости от нормальности распределения фактора и отклика
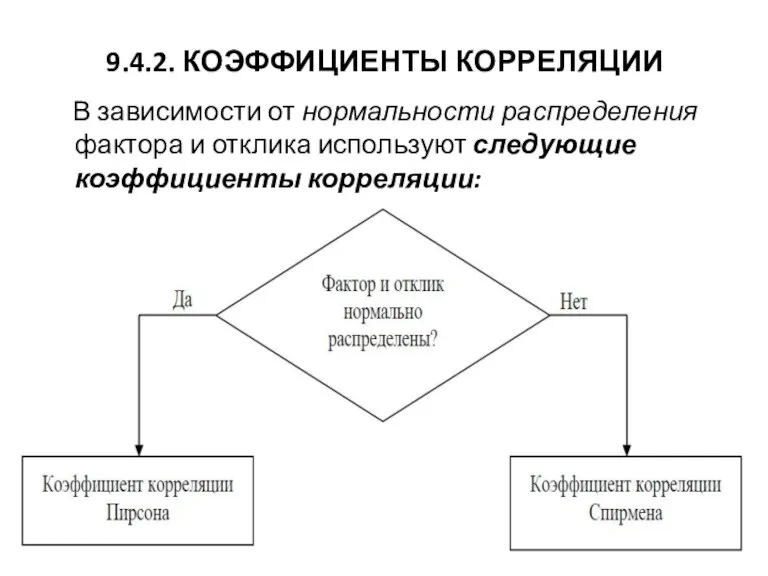
используют следующие коэффициенты корреляции:
Слайд 389.4.2.1. Коэффициент корреляции Пирсона

Слайд 399.4.2.1. Коэффициент корреляции Пирсона.
Особенности использования.

Слайд 409.4.2.1. Коэффициент корреляции Пирсона.
Особенности использования.
Для выборочной совокупности

Слайд 41Рассмотрим на предыдущем примере.
Данные об объемах продаж пиломатериалов по месяцам, млн.руб.

Слайд 42Разделим исходные данные на две части по 25 наблюдений и выясним, влияет
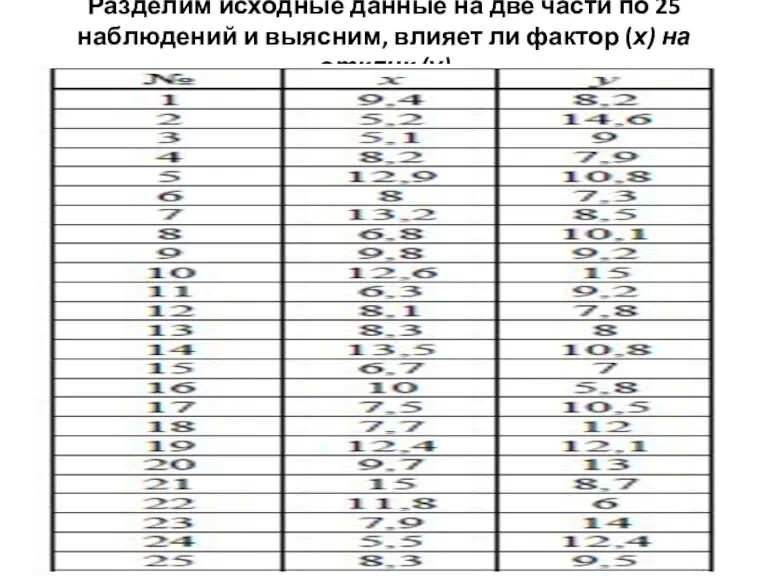
ли фактор (х) на отклик (у)
Слайд 44Расчетная таблица для вычисления коэффициента корреляции Пирсона
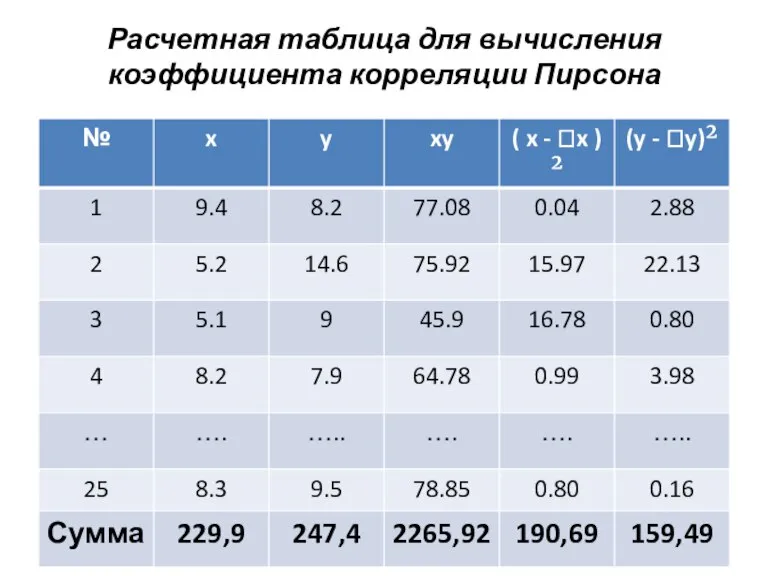
Слайд 469.4.2.2. Коэффициент корреляции Спирмена.
Особенности использования.

Слайд 479.4.2.2. Коэффициент корреляции Спирмена.
Ранжирование
Процедура ранжирования представляет собой упорядочивание значений по возрастанию.
Примеры
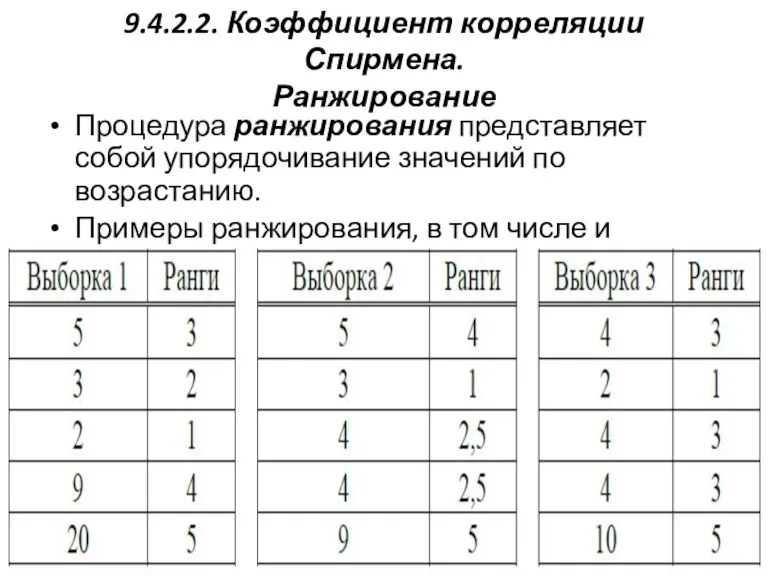
ранжирования, в том числе и выставление средних рангов.
Слайд 48Пример расчета корреляции Спирмена
Задание: Выяснить, влияют ли затраты на рекламу на
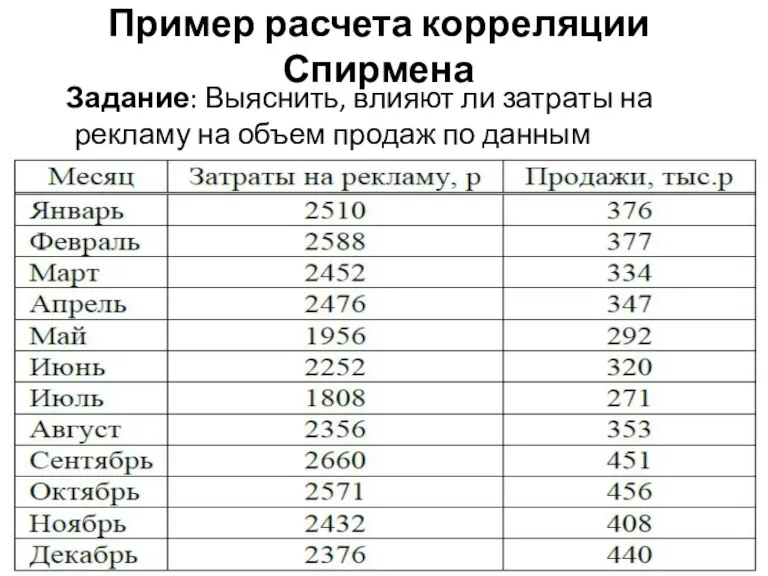
объем продаж по данным таблицы.
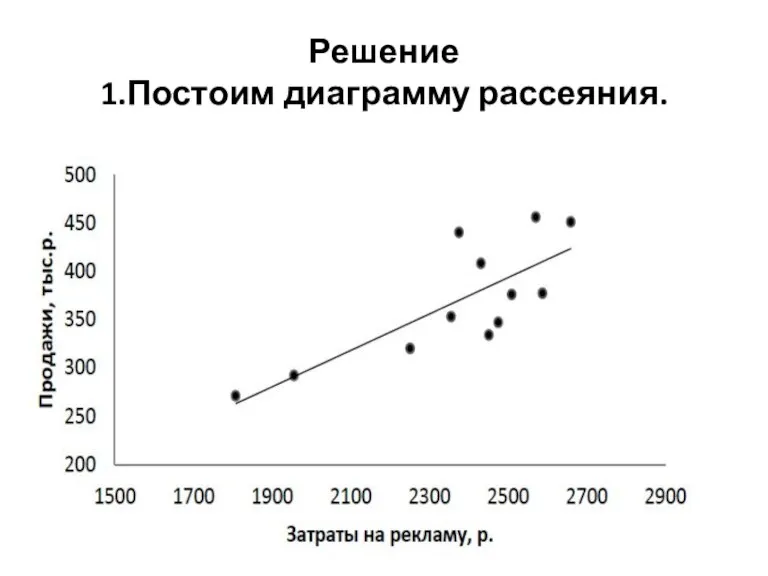
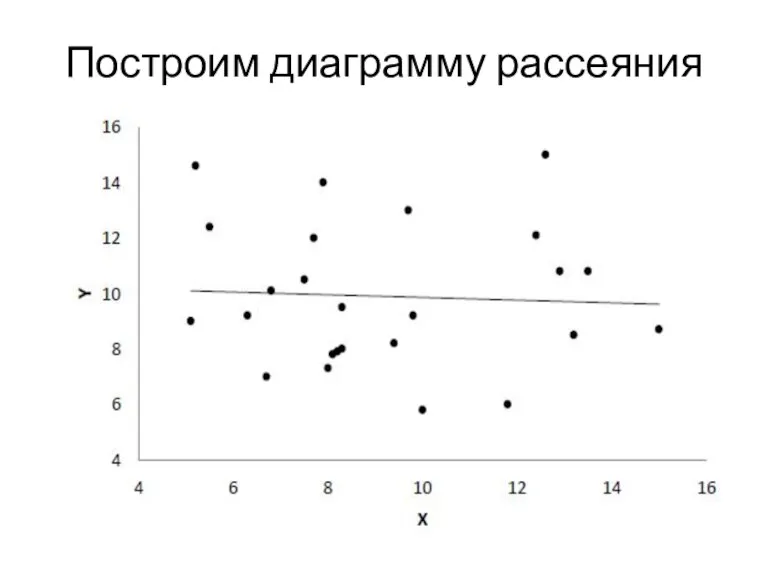
Слайд 49Решение
1.Постоим диаграмму рассеяния.
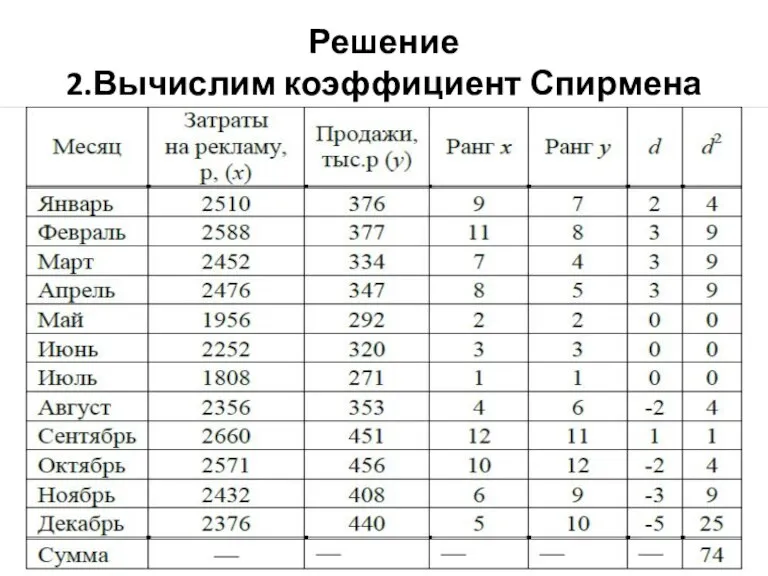
Слайд 50Решение
2.Вычислим коэффициент Спирмена
![Рекомендуемая литература: 1. М.Г. Назаров. Общая теория статистики. Учебник. [Электронный ресурс] :](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1142368/slide-1.jpg)














































 Основы анализа данных. Регрессионный анализ. (Лекция 6)
Основы анализа данных. Регрессионный анализ. (Лекция 6) Средняя скорость движения. Задание по графикам
Средняя скорость движения. Задание по графикам Линейные уравнения с одной переменной
Линейные уравнения с одной переменной Численные методы решения СЛАУ (часть 1)
Численные методы решения СЛАУ (часть 1) Прямые измерения, косвенные, совокупные и совместные
Прямые измерения, косвенные, совокупные и совместные РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания
РўР’РёРњРЎ_Лекция 3_Повторные независимые испытания Игра 3
Игра 3 Длина окружности. Площадь круга
Длина окружности. Площадь круга Сокращение дробей
Сокращение дробей Брейн-ринг. Математика
Брейн-ринг. Математика Факты о числе ПИ
Факты о числе ПИ Соединения с повторениями
Соединения с повторениями Выражение F
Выражение F Сложение чисел с разными знаками Волыхина Г.С.,
Сложение чисел с разными знаками Волыхина Г.С.,  Занимательная математика .Окружность
Занимательная математика .Окружность Цилиндр и конус. (Часть 2)
Цилиндр и конус. (Часть 2) Ряды Фурье
Ряды Фурье История дробей
История дробей Тетраэдр параллелепипед. 10 класс
Тетраэдр параллелепипед. 10 класс Геометрические фигуры: круг, квадрат, треугольник
Геометрические фигуры: круг, квадрат, треугольник Подготовка к контрольной работе
Подготовка к контрольной работе Множественный регрессионный анализ
Множественный регрессионный анализ Сплавы и смеси. Задачи 11 из ЕГЭ
Сплавы и смеси. Задачи 11 из ЕГЭ Чтение графика функции
Чтение графика функции Стандартные способы решения уравнений и неравенств (10-11 класс)
Стандартные способы решения уравнений и неравенств (10-11 класс) Эки эселенген бурчтун тригонометриялык функциялары
Эки эселенген бурчтун тригонометриялык функциялары Предел числовой последовательности и его свойства
Предел числовой последовательности и его свойства Степень с отрицательным показателем
Степень с отрицательным показателем