Свойство биссектрисы угла

Рассмотреть теорему о свойстве биссектрисы угла и её следствие.
Учить применять данные теоремы и следствие при решении задач.
Цели урока:

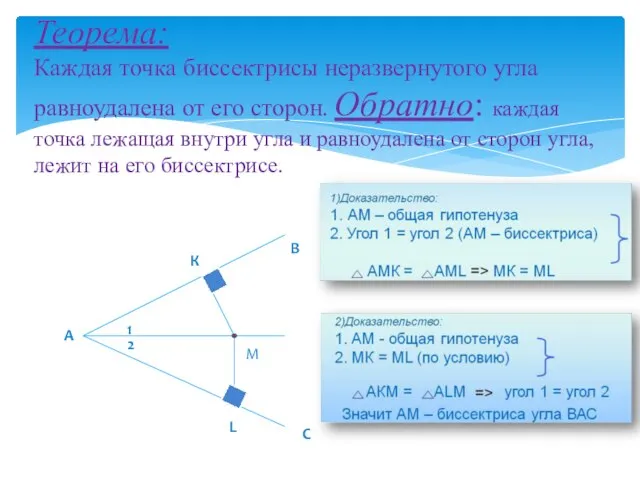
Теорема:
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: каждая точка лежащая внутри угла и равноудалена от сторон угла, лежит на его биссектрисе.
А
В
С
М
К
L
1
2

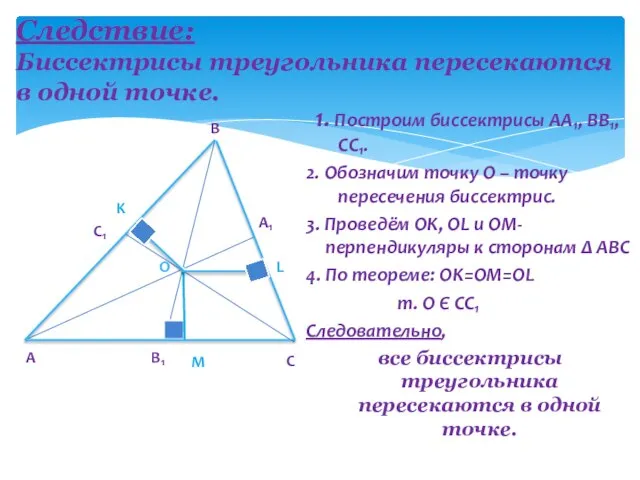
Следствие:
Биссектрисы треугольника пересекаются в одной точке.
1. Построим биссектрисы АА₁, BB₁, CC₁.
2. Обозначим точку O – точку пересечения биссектрис.
3. Проведём OK, OL и OM-перпендикуляры к сторонам Δ ABC
4. По теореме: OK=OM=OL
т. О Є СС₁
Следовательно,
все биссектрисы треугольника пересекаются в одной точке.
L
O

Задача
Cтороны угла А, равного 90°, касаются окружности с центром О и радиусом r, ОА = 14 дм. Найдите: r.
Решение:
Проведём радиусы OP и OH из центра окружности в точки касания.
2. AO – биссектриса угла
Δ AOP – прямоугольный.
По теореме Пифагора:
AO²=OP²+AP²
AO²=r²+r²,
2r²=14², r=7√2.
Ответ: r=7√2дм.