Слайд 2Теорема сложения вероятностей несовместных событий
Вероятность появления одного из двух, безразлично какого, события

из нескольких несовместных событий равна сумме их вероятностей
Р (А или В) = Р(А) + Р(В) ,
Сложение вероятностей справедливо не только для двух, но и для любого числа несовместных событий.
Важно!!! Если в условии задачи есть «ИЛИ» - только теорема сложения!!!
Слайд 5ЗАДАЧИ
1.На участке у врача 40 человек, четверо из которых больны гриппом, двое

– страдают гастритом, трое – ишемической болезнью сердца и шестеро – гипертонической болезнью. Найти вероятность того, что первый вызов врача на дом сделает больной гриппом или гипертонической болезнью. (0,25).
2. Стрелок стреляет по мишени, имеющей 3 области. Вероятность попасть в первую область равна 0,2; вероятности попасть во вторую и третью области равны соответственно 0,3 и 0.5. Найти вероятность того, что, выстрелив один раз, стрелок попадет в первую или в третью область. (0,7).
В отделении больницы проходят курс лечения 50 пациентов, имеющих заболевание L, 100 - с заболеванием N, и 350 - с заболеванием M. Какова вероятность того, что первый наугад осмотренный пациент будет иметь заболевание N или M? (0,9).
Слайд 6Теорема умножения вероятностей независимых событий
Вероятность совместного появления двух и более независимых событий

равна произведению в
ероятностей этих событий.
Р (А и В) = Р(А) x Р(В/А)
Важно!!! Если в условии задачи есть «НЕЗАВИСИМО» или это подразумевается- только теорема умножения независимых событий!!!
Слайд 10ЗАДАЧИ
1. Три врача независимо друг от друга осмотрели одного и того же

больного. Вероятность того, что первый врач установит верный диагноз, равна 0,8. Для второго и третьего врачей эти вероятности соответственно равны 0,7 и 0,9. Определите вероятность того, что все врачи поставят правильный диагноз. (0,5).
2. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна 0,8. Стрелок делает три выстрела. Определить вероятность того, что стрелок три раза попадет в мишень. (0,512).
3. Вероятность того, что стрелок при выстреле попадет в мишень, равна 0,9. Стрелок делает два выстрела. Определить вероятность того, что стрелок оба раза не попадет в мишень. (0,01).
Слайд 11Теорема умножения вероятностей зависимых событий
Вероятность совместного появления двух зависимых событий равна произведению

вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р (А и В) = Р(А) x Р(В/А)
эта теорема справедлива и для большего числа зависимых событий.
Условная вероятность Р(В/А) – это вероятность появления события В при условии, что событие А произошло.
Слайд 15ЗАДАЧИ
1. На приеме у врача находится 15 больных, 5 из которых больны

ветрянкой. Определить вероятность того, что 2 наугад выбранных пациента не больны ветрянкой? (0,43).
2. В укладке фельдшера скорой помощи находятся 20 шприцев, 5 из которых - 10-граммовые, остальные- 20 граммовые. На первом вызове было использовано 2 шприца. Определите вероятность того, что оба шприца были 10-граммовые.(0,05)
3. В урне находится 20 шаров: 4 белых и 16 красных. Определить вероятность одновременного изъятия из урны двух красных шаров.(0,63)














 Случайные события и вероятность Подготовила: Теленгатор С.В. учитель математики МОУ «Лицей №15» им. акад. Ю.Б. Харитона
Случайные события и вероятность Подготовила: Теленгатор С.В. учитель математики МОУ «Лицей №15» им. акад. Ю.Б. Харитона Основные способы преобразования графиков
Основные способы преобразования графиков Отбор корней в тригонометрических уравнениях. Уравнения, имеющие ограничения в области определения
Отбор корней в тригонометрических уравнениях. Уравнения, имеющие ограничения в области определения Логические схемы
Логические схемы Презентация на тему Учимся выполнять умножение 1 класс
Презентация на тему Учимся выполнять умножение 1 класс  Решение примеров с объяснением
Решение примеров с объяснением Математика вокруг нас
Математика вокруг нас Сумма углов треугольника
Сумма углов треугольника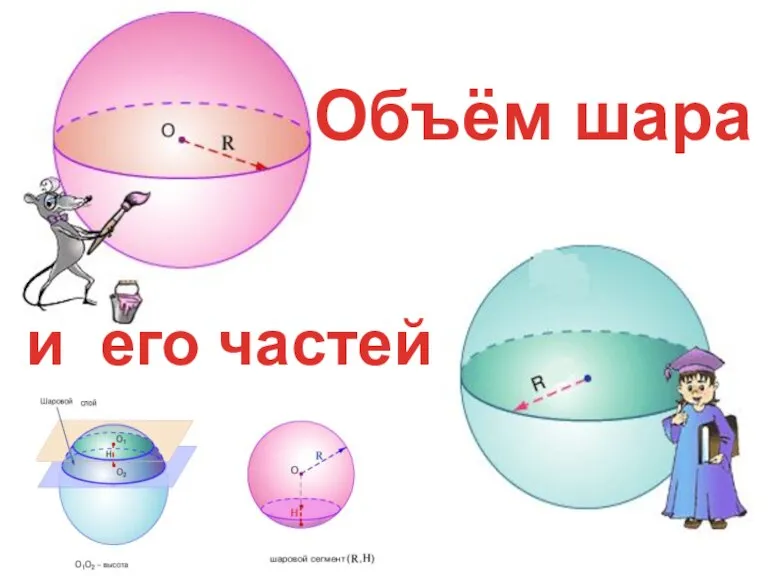 Объем шара
Объем шара Презентация на тему Нумерация чисел в пределах 10
Презентация на тему Нумерация чисел в пределах 10  Посади воздушные шары. Математика
Посади воздушные шары. Математика Случаи вычитания 15 -
Случаи вычитания 15 - Построение фронтальной диметрической и изометрической проекций
Построение фронтальной диметрической и изометрической проекций Деление с остатком. 4 класс
Деление с остатком. 4 класс Презентация на тему Решение систем неравенств (8 класс)
Презентация на тему Решение систем неравенств (8 класс)  Контрольная работа № 1. Вариант 0
Контрольная работа № 1. Вариант 0 Формула у=х2
Формула у=х2 Многоугольники. 9 класс
Многоугольники. 9 класс Теорема о вписанном угле. 8 класс
Теорема о вписанном угле. 8 класс Теорема Пифагора. Решение задач. Урок для 8 класса
Теорема Пифагора. Решение задач. Урок для 8 класса Коэффициент. 6 класс
Коэффициент. 6 класс Основы построения цифровых автоматов и систем анализа информационных процессов. Понятия СДНФ и СКНФ. Логико-вероятностное
Основы построения цифровых автоматов и систем анализа информационных процессов. Понятия СДНФ и СКНФ. Логико-вероятностное Интегрирование некоторых классов функций
Интегрирование некоторых классов функций Показательные неравенства
Показательные неравенства Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania
Lektsia_po_modulnoi_774_edinitse_4_Pervoobraznaya_i_neopredelennyi_774_integral_Metody_integrirovania Пропорциональность площадей
Пропорциональность площадей Метод резолюций в алгебре высказываний
Метод резолюций в алгебре высказываний Кластерный анализ
Кластерный анализ