Теория фракталов

Математическое выражение самоподобия:

История фрактальной геометрии
Связана с именами таких математиков, как Вейерштрасс, Кантор, Пеано, Хаусдорф, Безикович, Кох, Серпинский и др.
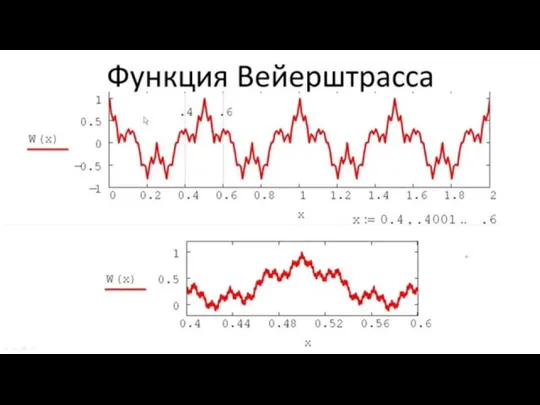
Вейерштрасс впервые ввёл в обращение непрерывную, но нигде не дифференцируемую функцию в 1872 году.
Гастон Жюлиа описал в 1918 году динамические фракталы.
Хаусдорф в 1919 году ввёл понятие о дробной размерности множеств и привёл первые примеры таких множеств.

Функция Вейерштрасса

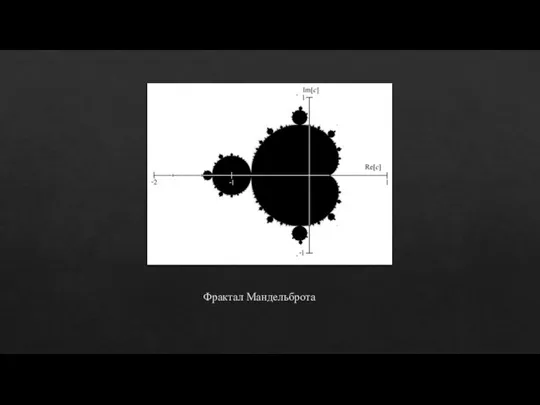
Термин «фрактал» был введён в 1975 году Бенуа Мандельбротом. Один из его самых важных трудов–«Фрактальная геометрия природы».

Фрактал Мандельброта

Построение кривой Коха

Фрактал (от лат. fractus—дробный)
Множество F является фракталом, если:
1) Имеет тонкую структуру, т.е. детали произвольно малых масштабов
2) Является слишком нерегулярным для того, чтобы описываться традиционной геометрией, как локально, так и глобально
3) Обладает некоторым самоподобием, возможно приблизительным или статистическим
4) Фрактальная размерность F больше, чем её топологическая размерность
5) Во многих интересных случаях определяется очень просто, возможно рекурсивно

Бронхи

Застенчивая крона деревьев

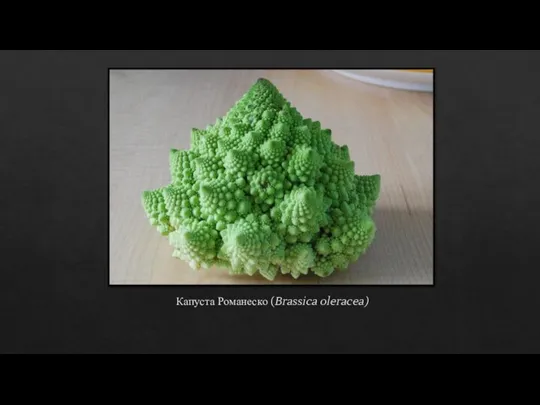
Капуста Романеско (Brassica oleracea)

Кристаллическая структура минерала турмалина