Содержание
- 2. У Г А Т У Лекционное занятие Рекомендовано для обучающихся по направлениям Уфимский государственный авиационный технический
- 3. У Г А Т У План Уфимский государственный авиационный технический университет Множества и элементы множеств. Сравнение
- 4. У Г А Т У 1. Множества и элементы множеств Уфимский государственный авиационный технический университет Лекционное
- 5. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 1. Множества и элементы
- 6. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 1. Множества и элементы
- 7. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 1. Множества и элементы
- 8. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Кроме того, в теории
- 9. У Г А Т У Уфимский государственный авиационный технический университет 2. Сравнение множеств Лекционное занятие
- 10. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 2. Сравнение множеств Множество
- 11. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Отношения между подмножествами удобно
- 12. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 2. Сравнение множеств
- 13. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 2. Сравнение множеств
- 14. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 3. Операции над множествами
- 15. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 3. Операции над множествами
- 16. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Объединение. Объединение множеств характеризуется
- 17. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Разность. Разностью множеств A
- 18. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Зеркально: разностью множеств B
- 19. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Декартово произведение множеств Декартовым
- 20. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Зеркально: декартовым произведением множеств
- 21. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 4. Диаграммы Эйлера –
- 22. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие Диаграммы Эйлера-Венна – это
- 23. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 4. Диаграммы Эйлера-Венна
- 24. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 5. Свойства операций над
- 25. У Г А Т У Уфимский государственный авиационный технический университет Лекционное занятие 5. Свойства операций над
- 27. Скачать презентацию
























 Множественный регрессионный анализ
Множественный регрессионный анализ Подобные треугольники
Подобные треугольники Бесплатный интенсив по тригонометрии
Бесплатный интенсив по тригонометрии Задачи с обыкновенными дробями
Задачи с обыкновенными дробями Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Простейшие тригонометрические уравнения. Частные случаи. Уравнения, приводимые к алгебраическим
Простейшие тригонометрические уравнения. Частные случаи. Уравнения, приводимые к алгебраическим Предел функции (часть 4)
Предел функции (часть 4)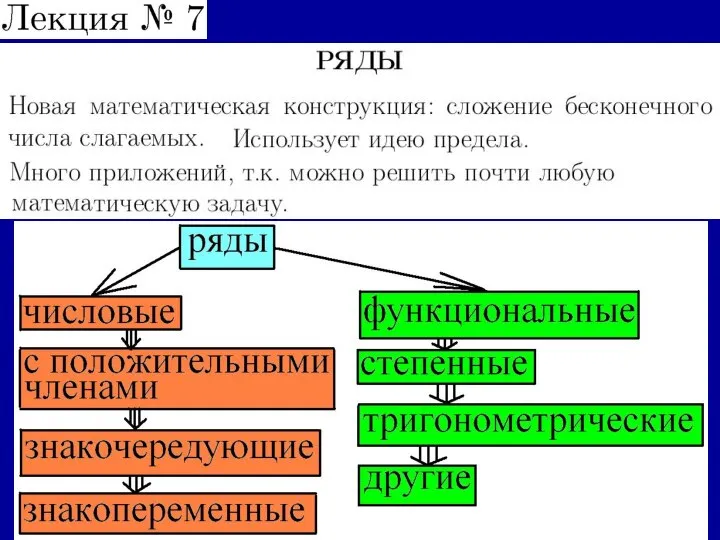 Числовые ряды
Числовые ряды Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) 764fab9c-7974-40e4-8362-2c4469fed7e2
764fab9c-7974-40e4-8362-2c4469fed7e2 Приёмы внетабличного умножения и деления. Закрепление
Приёмы внетабличного умножения и деления. Закрепление Приёмы устных вычислений вида 260+310, 670-140
Приёмы устных вычислений вида 260+310, 670-140 Комплексные числа
Комплексные числа Косинус угла
Косинус угла Решение задач на движение
Решение задач на движение Решение систем неравенств второй степени с двумя переменными
Решение систем неравенств второй степени с двумя переменными Найди соседей. Дидактическая игра
Найди соседей. Дидактическая игра Интегрирование на подмножествах (Кратный интеграл)
Интегрирование на подмножествах (Кратный интеграл) Трапеция
Трапеция Путешествие с колобком к новогодней ёлке (начальная школа)
Путешествие с колобком к новогодней ёлке (начальная школа) Правильные многогранники
Правильные многогранники Применение производной к исследованию функции
Применение производной к исследованию функции Числовые головоломки
Числовые головоломки Урок по геометрии
Урок по геометрии Решение уравнений
Решение уравнений Векторное кодирование графической информации
Векторное кодирование графической информации Интересная математика
Интересная математика Графики степенных функций
Графики степенных функций