- Главная
- Математика
- Тригонометрические функции, их графики и свойства

Содержание
Слайд 2ФУНКЦИЯ y = sin x
График функции y = sin x
Свойства функции:
D(sin x)
ФУНКЦИЯ y = sin x
График функции y = sin x
Свойства функции:
D(sin x)
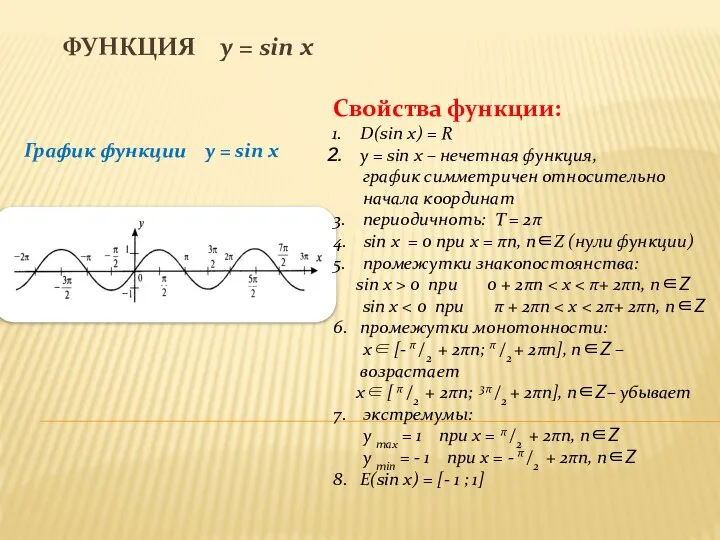
= R
y = sin x – нечетная функция,
график симметричен относительно
начала координат
3. периодичноть: T = 2π
4. sin x = 0 при х = πn, n∈Z (нули функции)
5. промежутки знакопостоянства:
sin x > 0 при 0 + 2πn < x < π+ 2πn, n∈Z
sin x < 0 при π + 2πn < x < 2π+ 2πn, n∈Z
6. промежутки монотонности:
x∈ [- π /2 + 2πn; π /2 + 2πn], n∈Z – возрастает
x∈ [ π /2 + 2πn; 3π /2 + 2πn], n∈Z– убывает
7. экстремумы:
y max = 1 при х = π /2 + 2πn, n∈Z
y min = - 1 при х = - π /2 + 2πn, n∈Z
8. E(sin x) = [- 1 ; 1]
y = sin x – нечетная функция,
график симметричен относительно
начала координат
3. периодичноть: T = 2π
4. sin x = 0 при х = πn, n∈Z (нули функции)
5. промежутки знакопостоянства:
sin x > 0 при 0 + 2πn < x < π+ 2πn, n∈Z
sin x < 0 при π + 2πn < x < 2π+ 2πn, n∈Z
6. промежутки монотонности:
x∈ [- π /2 + 2πn; π /2 + 2πn], n∈Z – возрастает
x∈ [ π /2 + 2πn; 3π /2 + 2πn], n∈Z– убывает
7. экстремумы:
y max = 1 при х = π /2 + 2πn, n∈Z
y min = - 1 при х = - π /2 + 2πn, n∈Z
8. E(sin x) = [- 1 ; 1]
Слайд 3ФУНКЦИЯ y = cos x
График функции y = cos x
Свойства функции:
D(cos x)
ФУНКЦИЯ y = cos x
График функции y = cos x
Свойства функции:
D(cos x)
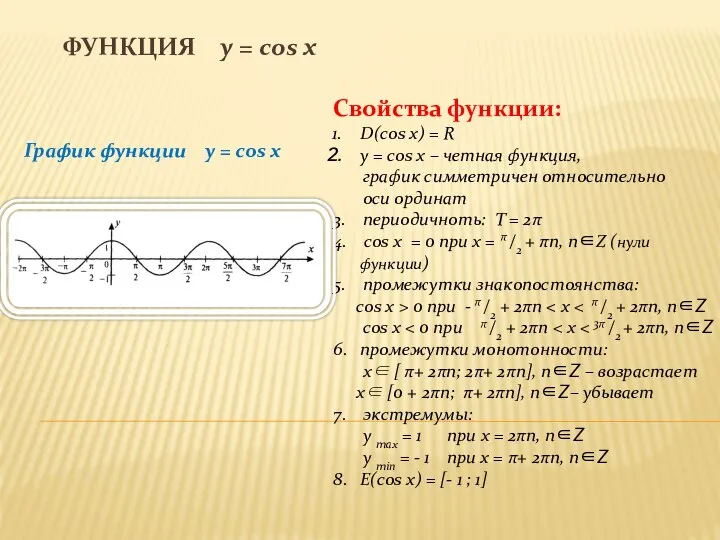
= R
y = cos x – четная функция,
график симметричен относительно
оси ординат
3. периодичноть: T = 2π
4. cos x = 0 при х = π /2 + πn, n∈Z (нули функции)
5. промежутки знакопостоянства:
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, n∈Z
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, n∈Z
6. промежутки монотонности:
x∈ [ π+ 2πn; 2π+ 2πn], n∈Z – возрастает
x∈ [0 + 2πn; π+ 2πn], n∈Z– убывает
7. экстремумы:
y max = 1 при х = 2πn, n∈Z
y min = - 1 при х = π+ 2πn, n∈Z
8. E(cos x) = [- 1 ; 1]
y = cos x – четная функция,
график симметричен относительно
оси ординат
3. периодичноть: T = 2π
4. cos x = 0 при х = π /2 + πn, n∈Z (нули функции)
5. промежутки знакопостоянства:
cos x > 0 при - π /2 + 2πn < x < π /2 + 2πn, n∈Z
cos x < 0 при π /2 + 2πn < x < 3π /2 + 2πn, n∈Z
6. промежутки монотонности:
x∈ [ π+ 2πn; 2π+ 2πn], n∈Z – возрастает
x∈ [0 + 2πn; π+ 2πn], n∈Z– убывает
7. экстремумы:
y max = 1 при х = 2πn, n∈Z
y min = - 1 при х = π+ 2πn, n∈Z
8. E(cos x) = [- 1 ; 1]
Слайд 4ФУНКЦИЯ y = tg x
График функции y = tg x
Свойства функции:
D(tg x)
ФУНКЦИЯ y = tg x
График функции y = tg x
Свойства функции:
D(tg x)

= x∈ R/ π /2 + πn, n∈Z
y = tg x – нечетная функция
график симметричен относительно
начала координат
3. периодичноть: T = π
4. tg x = 0 при х = πn, n∈Z (нули функции)
5. промежутки знакопостоянства:
tg x > 0 при 0 + πn < x < π /2 + πn, n∈Z
tg x < 0 при - π /2 + πn < x < 0 + πn, n∈Z
6. промежутки монотонности:
x∈ [- π /2 + πn; π /2 + πn], n∈Z – возрастает
экстремумов нет
E(tg x) = R
y = tg x – нечетная функция
график симметричен относительно
начала координат
3. периодичноть: T = π
4. tg x = 0 при х = πn, n∈Z (нули функции)
5. промежутки знакопостоянства:
tg x > 0 при 0 + πn < x < π /2 + πn, n∈Z
tg x < 0 при - π /2 + πn < x < 0 + πn, n∈Z
6. промежутки монотонности:
x∈ [- π /2 + πn; π /2 + πn], n∈Z – возрастает
экстремумов нет
E(tg x) = R
 Состав числа 9
Состав числа 9 Логарифмы
Логарифмы Интеллектуальная игра по математике: ТОК. Для учащихся 8-го класса
Интеллектуальная игра по математике: ТОК. Для учащихся 8-го класса Презентация на тему Задачи на приведение к единице (3 класс)
Презентация на тему Задачи на приведение к единице (3 класс)  Элективный курс. Алгебра 11 класс. Уроки 10
Элективный курс. Алгебра 11 класс. Уроки 10 Сумма углов треугольника. Виды треугольников
Сумма углов треугольника. Виды треугольников izmerenie_otrezkov_7_klass
izmerenie_otrezkov_7_klass Калькуляционная карточка. Тесто заварное
Калькуляционная карточка. Тесто заварное Задачи на движение
Задачи на движение Статистические гипотезы и их проверка
Статистические гипотезы и их проверка Деление круглых сотен на число 100
Деление круглых сотен на число 100 Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Шахматы и математика
Шахматы и математика Методы решения оптимизационных задач
Методы решения оптимизационных задач Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Приёмы сложения однозначных чисел с переходом через десяток
Приёмы сложения однозначных чисел с переходом через десяток Модели решения функциональных и вычислительных задач. Методы и технологии моделирования
Модели решения функциональных и вычислительных задач. Методы и технологии моделирования Презентация на тему Деление суммы на число (3 класс)
Презентация на тему Деление суммы на число (3 класс)  Производная. Тест по алгебре
Производная. Тест по алгебре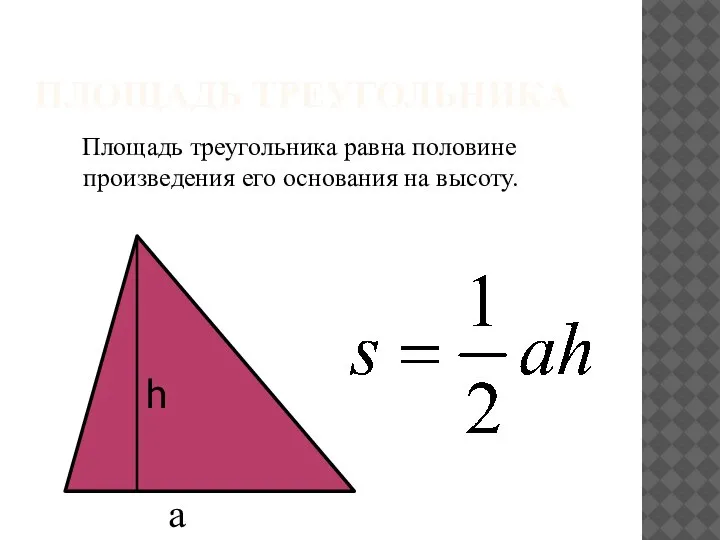 Площадь треугольника
Площадь треугольника Взвешивания. Домашнее задание 1 класс
Взвешивания. Домашнее задание 1 класс Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Руководитель кружка по математике для 7 класса
Руководитель кружка по математике для 7 класса Элементы аналитической геометрии на плоскости
Элементы аналитической геометрии на плоскости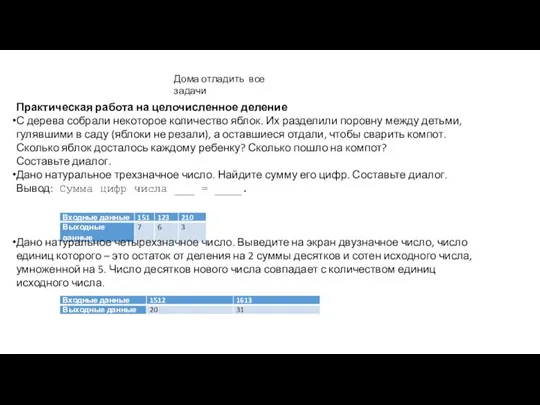 Практическая работа на целочисленное деление
Практическая работа на целочисленное деление Геометрические преобразования в пространстве
Геометрические преобразования в пространстве Реальная математика. Геометрия. ГИА-2014
Реальная математика. Геометрия. ГИА-2014