Задачи по теме: Смеси и сплавы. Подготовка к ЕГЭ. Профильный уровень. №11

Имеются два сосуда. Первый содержит 100 кг, а второй — 90 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 66% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 67% кислоты.
Сколько килограммов кислоты содержится в первом сосуде?
№11

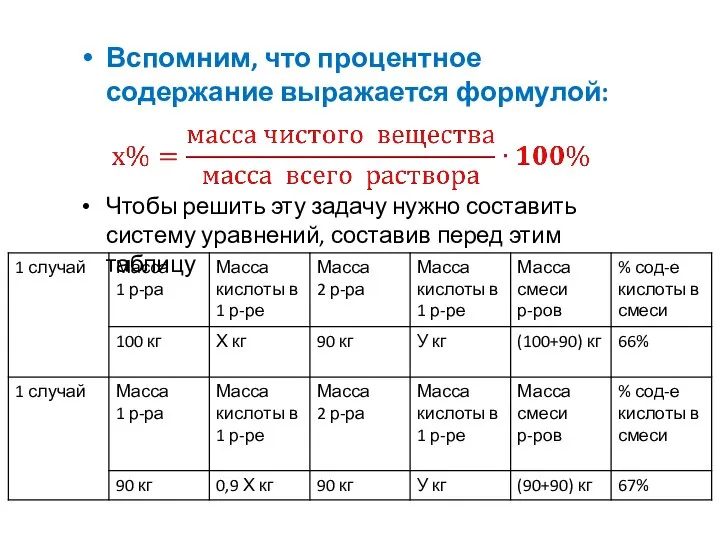
Вспомним, что процентное содержание выражается формулой:
Чтобы решить эту задачу нужно составить систему уравнений, составив перед этим таблицу

Имеются два сосуда. Первый содержит 100 кг, а второй — 90 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 66% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 67% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Решение
Пусть х кг кислоты содержится в первом сосуде,
а y кг кислоты содержится во втором сосуде,
тогда (x + y) кг – масса кислоты в первом растворе,
И масса первого раствора будет:
100 + 90 = 190 (кг)
Т.К получится раствор, содержащий 66% кислоты, то составим 1 уравнение:
№11

2 случай .
Возьмем равные массы двух веществ.
Берем максимальную величину меньшего по
массе раствора ( 90 кг ) и равную величину меньшего
по массе раствора от первого: от 100 кг берем 90 кг
т.к. второй раствор весит 90 кг
90 + 90 = 180(кг) - масса нового раствора
(0,9x + y) кг– масса кислоты
Т.К получится раствор, содержащий 67% кислоты, то составим 2 уравнение:

Составим систему уравнений
X = 1254 -1206
X = 48
48 кг кислоты содержится в первом сосуде

Смешав 77-процентный и 79-процентный растворы кислоты и добавив 10 кг чистой воды, получили 70-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 77-процентного раствора использовали для получения смеси?
№11
Решение
Пусть х кг будет масса первого раствора, а масса чистого вещества будет 0,77х (по условию)
Масса второго вещества пусть будет у кг, а масса чистого вещества будет 0,79у (по условию)
Так как эти два раствора перелили в один общий сосуд и добавили еще 10 кг чистой воды то общая масса всего раствора: (x+y+10) кг

Т.к. получили 70-процентный раствор кислоты, составим первое уравнение системы:
Рассмотрим 2 случая
По условию сказано, что если бы вместо 10 кг воды добавили 10 кг 50%раствора той же кислоты, то получили бы 75% раствор кислоты
Составим второе уравнение системы:

Составим систему уравнений
:2

7∙(125 - 2у) + 9у = 700
875 - 14у + 9у = 700
- 5у = -175
у = 35
х = 125 - 2∙35
х = 55
55 кг -77-процентного раствора
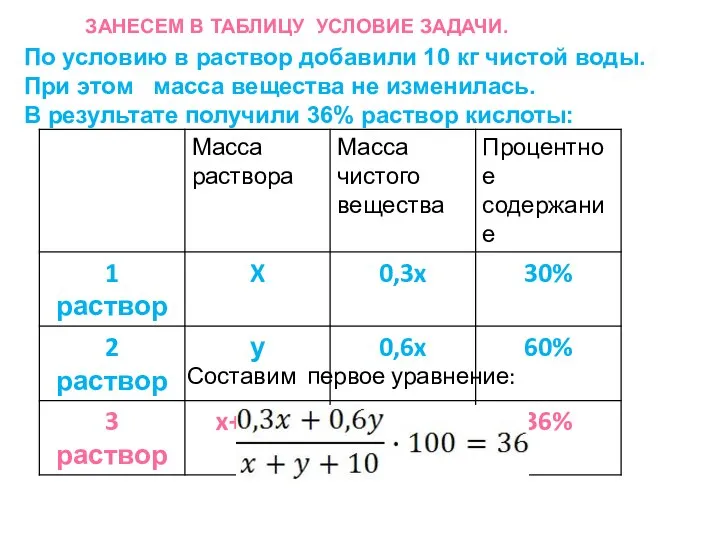
В ответе нужно записать, сколько килограммов 77% раствора использовали для получения смеси, то есть X:

Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты.
Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты.
Сколько килограммов 30-процентного раствора использовали для получения смеси?
№11

ЗАНЕСЕМ В ТАБЛИЦУ УСЛОВИЕ ЗАДАЧИ.
Составим первое уравнение:
По условию в раствор добавили 10 кг чистой воды. При этом масса вещества не изменилась. В результате получили 36% раствор кислоты:

Если бы вместо 10 кг добавили 10 кг 50% раствора той же кислоты то получили бы 41% раствор кислоты
Составим второе уравнение

Составим систему уравнений
:(-6)