Содержание
- 2. Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и
- 3. Историческая справка Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа
- 4. XVII век: Блез Паскаль Пьер де Ферма
- 5. Я́коб Берну́лли Бернулли предложил классическое определение вероятности случайного события. Он также изложил правила подсчёта вероятности для
- 6. Русская школа Пафну́тий Льво́вич Чебышёв Андре́й Андре́евич Ма́рков Алекса́ндр Миха́йлович Ляпуно́в
- 7. На вероятностных методах основаны: 1) Квантовая механика 2) Генетика 3) Математическая статистика 4) Теория информации 5)
- 8. Теория вероятностей в программировании Базы данных (регистрации, фильтрации) Теория игр и game development (случайные встречи, срабатывания
- 9. Основные понятия
- 10. Что такое событие? Под событием понимают то, относительно чего после некоторого момента времени можно сказать одно
- 11. Виды случайных событий: Совместные и несовместные Единственно и не единственно возможные Полные группы Противоположные, не являющиеся
- 12. Классическое определение вероятности Определение: Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов,
- 13. Свойство вероятности противоположных событий Вероятность Р(А) некоторого события События А и В называются противоположными, если всякое
- 14. Занимательные открытия и теории, появившиеся благодаря теории вероятностей
- 15. Кот Шрёдингера Мысленный эксперимент, предложенный австрийским физиком-теоретиком, одним из создателей квантовой механики, Эрвином Шрёдингером, которым он
- 16. ДНК - компьютер В 1994 году Леонард Адлеман, профессор университета Южной Калифорнии, продемонстрировал, что с помощью
- 17. Теорема Шеннона Основана на понятии энтропии – меры неопределённости некоторой системы (например, какого-либо опыта, который может
- 18. Вероятности в повседневной жизни
- 22. Скачать презентацию



















 Многоугольники в нашей жизни
Многоугольники в нашей жизни Разложение вектора по двум неколлинеарным векторам
Разложение вектора по двум неколлинеарным векторам Квадратичная функция. Наглядно-методическое пособие. 9 класс
Квадратичная функция. Наглядно-методическое пособие. 9 класс XII командный турнир по математике Математические бои
XII командный турнир по математике Математические бои Пирамида. Элементы пирамиды. Поверхность пирамиды
Пирамида. Элементы пирамиды. Поверхность пирамиды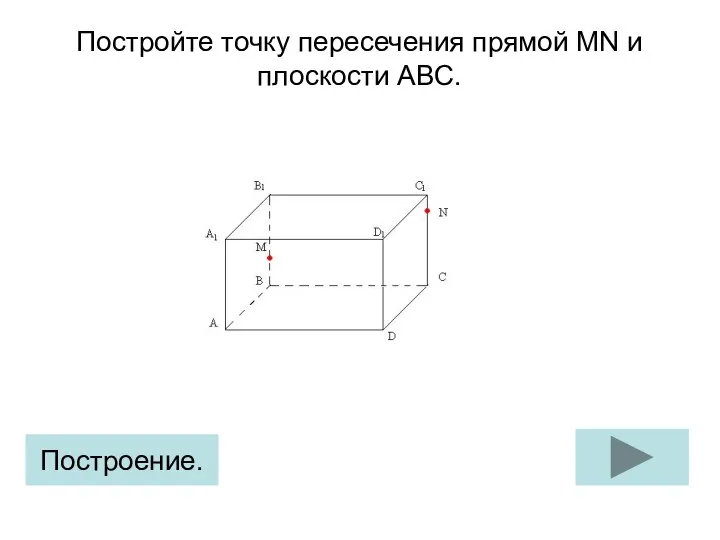 Точка пересечения прямой MN и плоскости ABC. Построение (задание 2)
Точка пересечения прямой MN и плоскости ABC. Построение (задание 2) Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс
Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс Переводчицы. Задача
Переводчицы. Задача Подумай. Вопросы. Тесты
Подумай. Вопросы. Тесты Вычисления вида 32 + 8, 40 – 8
Вычисления вида 32 + 8, 40 – 8 Следствия из теорем синусов и косинусов
Следствия из теорем синусов и косинусов Условная оптимизация. Лекция 11
Условная оптимизация. Лекция 11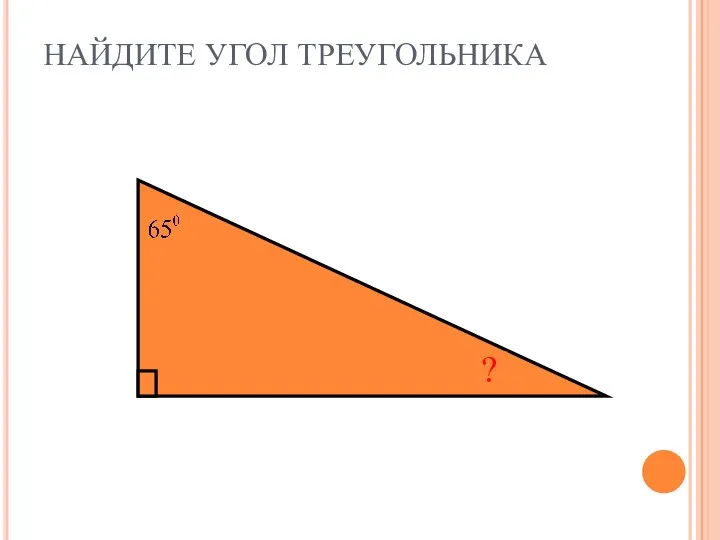 Нахождение угла треугольника
Нахождение угла треугольника Существование треугольника, равного данному (7 класс)
Существование треугольника, равного данному (7 класс) Окружность и круг
Окружность и круг Аттестационная работа. Сослужит ли добрую службу математика экологии
Аттестационная работа. Сослужит ли добрую службу математика экологии Математика и Незнайка. Математическая сказка
Математика и Незнайка. Математическая сказка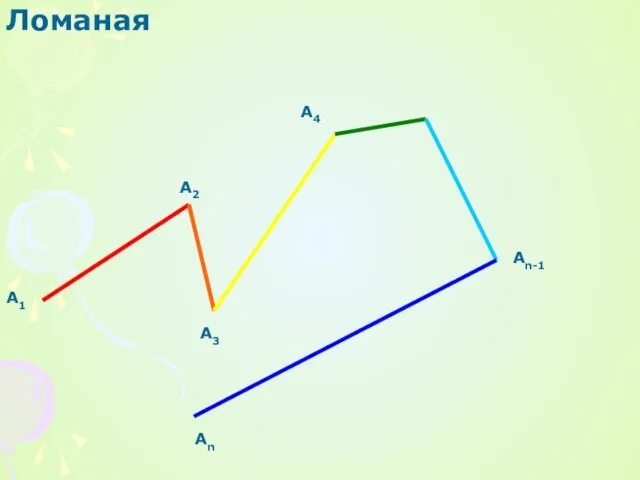 Презентация на тему Ломаная
Презентация на тему Ломаная  Основы геометрии
Основы геометрии История дифференциального исчисления
История дифференциального исчисления Построение графиков функций
Построение графиков функций Цифра в 21 веке
Цифра в 21 веке Карточки по математике
Карточки по математике Окружность и длина окружности
Окружность и длина окружности Прямоугольник. Ось симметрии
Прямоугольник. Ось симметрии Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Методы решения логарифмических уравнений. 11 класс
Методы решения логарифмических уравнений. 11 класс Площадь параллелограмма и ромба
Площадь параллелограмма и ромба