Системы принятия решений

Оценки экстремума

Оценки экстремума
т.е. погрешность решения задачи, невозможно.
Возможность получения оценок экстремума по конечному числу испытаний зависит от свойств класса функций, которому принадлежит минимизируемая функция, или, другими словами, от априорной информации о функции . Фактически известны лишь два широких класса функций, допускающих построение таких оценок: класс одномерных унимодальных функций и класс функций, удовлетворяющих условию Липшица (в общем случае многомерных и многоэкстремальных).

Оценки экстремума для унимодальных функций
Пример. Унимодальная функция на отрезке [0,8].

Построение миноранты
Задание
Построить для константы Липшица миноранту функции
на интервале [0,4] по точкам испытаний
и указать оценку величины глобального минимума

Оптимальность алгоритмов оптимизации
Рассмотрим класс алгоритмов , предназначенных для решения задач оптимизации функций .
Вводится вещественная функция V(ϕ,s) - критерий эффективность решения задачи минимизации функции с помощью метода
Критерии эффективности метода s на классе
или
P(ϕ) — некоторое распределение вероятностей, заданных на классе измеримых подмножеств множества .
Оптимальный алгоритм :

Оптимальность алгоритмов оптимизации
ε-оптимальный алгоритм оптимизации :
Наилучший (последовательно-оптимальный алгоритм ) оптимизации (А.Г.Сухарев) - алгоритм, наилучшим образом использующий апостериорную (поисковую) информацию.

Одношаговая оптимальность
Существуют значительные трудности в создании алгоритмов в соответствии с принципами оптимальности (1.28) или (1.29). Чтобы преодолеть эти трудности, можно попытаться упростить понятие оптимальности. Такую возможность предоставляет принцип одношаговой оптимальности, когда мы требуем оптимального поведения алгоритма не в течение всего процесса оптимизации, а только на один шаг вперед, т.е. при выборе точки очередного испытания.
Чтобы кратко описать модель одношагово-оптимального алгоритма, вспомним ряд обозначений, принятых в общей схеме численного метода оптимизации (1.9)-(1.14).
и мы можем утверждать, что целевая функция принадлежит классу

Одношаговая оптимальность

Асимптотическая оптимальность
Рассмотрим алгоритм такой, что на каждом шаге его усечение

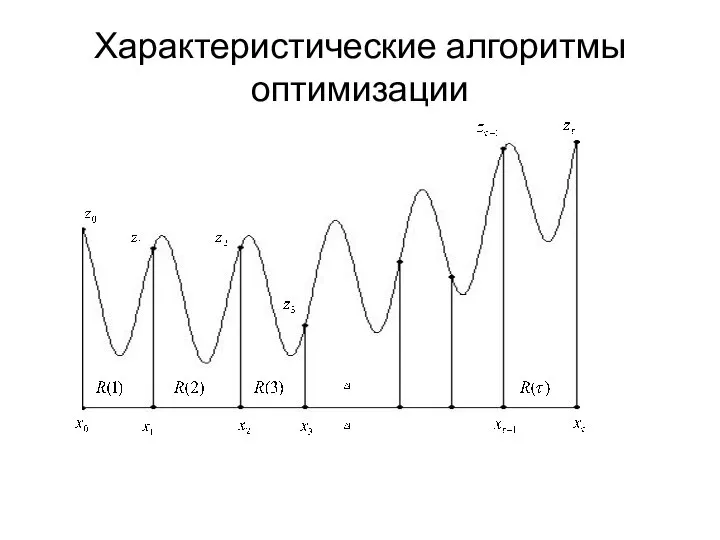
Характеристические алгоритмы оптимизации
1. Задать множество
конечного числа точек области , полагая, что
, все координаты предшествующих испытаний
множество упорядочено (нижним индексом) по возрастанию координаты, т.е.
и сопоставить точкам множества значения

Характеристические алгоритмы оптимизации
2. Каждому интервалу , , поставить в соответствие число , называемое характеристикой этого интервала.
3. Определить интервал , которому соответствует максимальная характеристика , т.е.
4. Провести очередное испытание в точке
и вычислить значение

Характеристические алгоритмы оптимизации

Примеры характеристических алгоритмов
Два первых испытания проводятся в точках и ,
характеристическое правило вступает в действие, начиная с k=2, при этом множество состоит только из точек испытаний, т.е.
и, следовательно,
Метод последовательного сканирования (перебор).

Методы Пиявского и Стронгина
Метод Пиявского (метод ломаных)

Метод Кушнера
Точка очередного испытания

Алгоритм глобального поиска без вычислений на концах интервала

Алгоритм глобального поиска без вычислений на концах интервала
Точка очередного испытания
- параметр метода

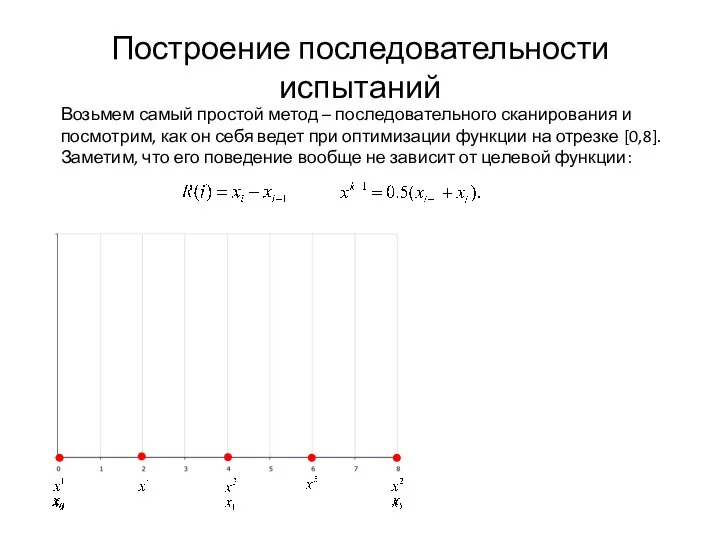
Построение последовательности испытаний
Возьмем самый простой метод – последовательного сканирования и посмотрим, как он себя ведет при оптимизации функции на отрезке [0,8].
Заметим, что его поведение вообще не зависит от целевой функции:

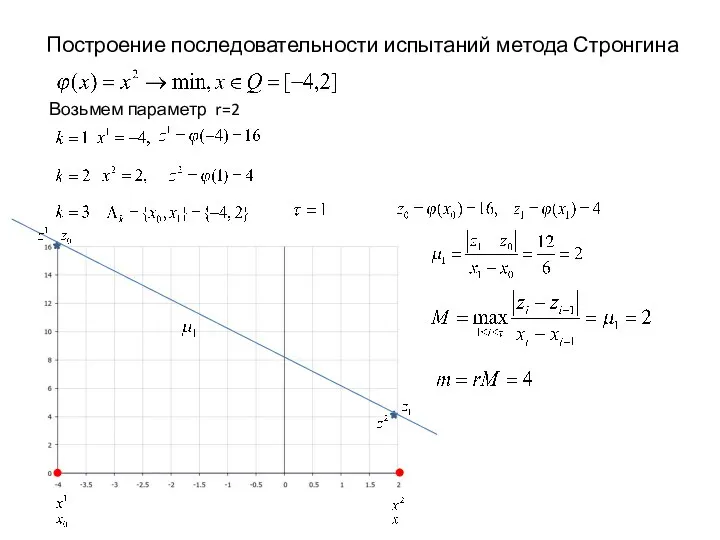
Возьмем параметр r=2
Построение последовательности испытаний метода Стронгина

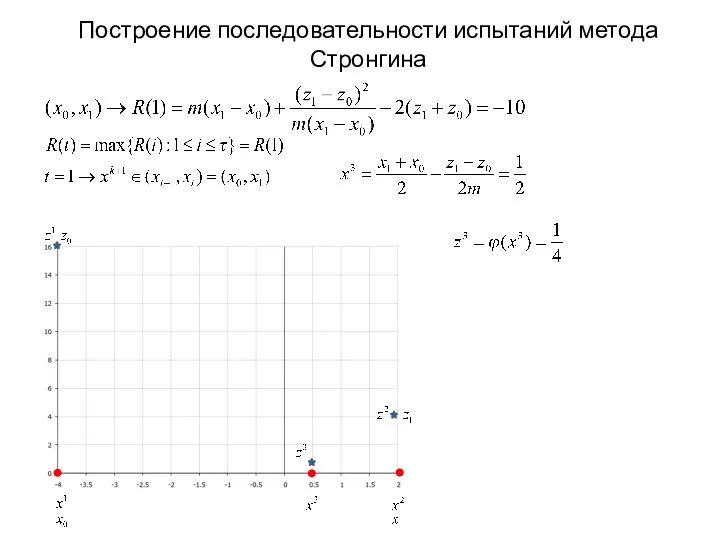
Построение последовательности испытаний метода Стронгина