Описание методов статистической обработки данных

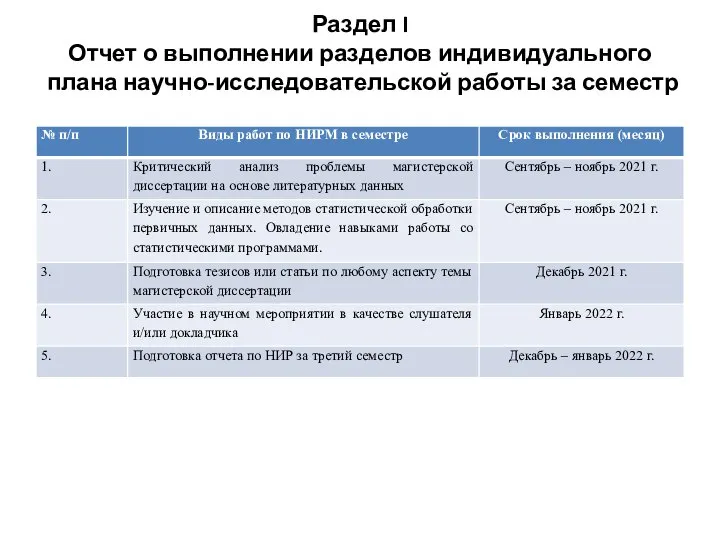
Раздел I
Отчет о выполнении разделов индивидуального плана научно-исследовательской работы за семестр

Раздел II
Содержательный отчет о результатах научно-исследовательской работы за семестр
Пункт 1 выполнен. Приложение 1.
Пункт 2 выполнен. Приложение 2.
Пункт 3 выполнен. Подготовлены тезисы на тему «Радиочувствительность водорослевых культур scenedesmus quadricauda, выделенных из радиоактивно загрязненных водоемов по «Маяк»». Публикация в сборнике «Образование магистров: проблемы и перспективы развития: тезисы докладов IV Всероссийской конференции» (23-25 ноября 2020 г., Челябинск) / отв. за вып. О.И. Саломатова. Челябинск: Изд-во Челяб. гос. ун-та, 2020. 403 с. Они приведены в приложении 3.
Пункт 4. 12-15 октября 2021 принял участие в VIII Съезде по радиационным исследованиям, состоявшемся в Москве и проходившего через Zoom. Ознакомился с материалами, особое внимание уделил секции №11 (радиобиология неионизирующих излучений).

Критический анализ проблемы магистерской диссертации на основе литературных данных
Проблема этого исследования (генотоксическое действие комбинированного электромагнитного и γ-излучения на клетки лука) стоит весьма остро, так как в настоящее время развиваются технологии, серьезно воздействующие на биосферу, следовательно, необходимо исследование тех организмов, которые могут служить биоиндикаторами радиационного и электромагнитного воздействия.
Проблема, поднятая в магистерской диссертации, разбирается в работах российских и зарубежных ученых.

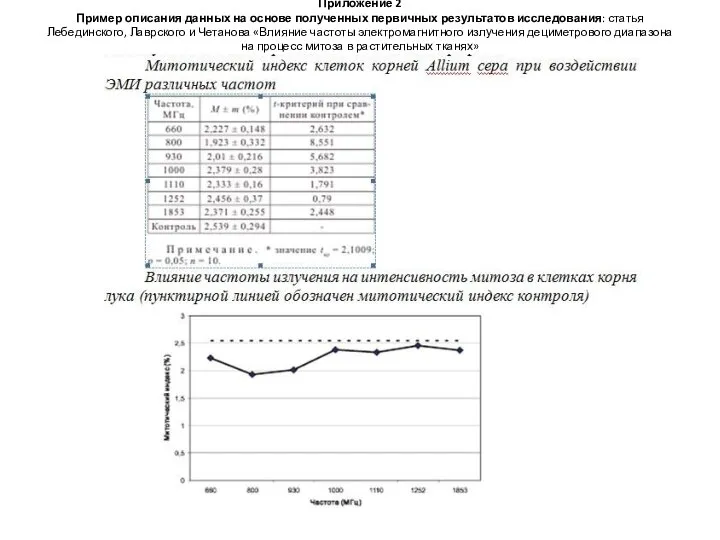
Исследование российских ученых Лебединского и Лаврского. Анализ полученных данных позволяет говорить о существовании нелинейной зависимости между частотой электромагнитного излучения и его митотоксическом влиянии на тестовые объекты. Значительным митотоксическим эффектом обладает излучение в диапазоне 800-930 МГц, что соответствует стандарту сотовой связи GSM 850/900.

Болсуновский и Дементьев исследовали влияние γ-излучения на степень повреждений ядерной ДНК проростков лука (Allium-test) методом ДНК-комет. Впервые обнаружили разрывы ДНК в клетках проростков лука при малых дозах облучения (≤0,1 Гр). Для дозовой зависимости параметров повреждений ДНК отмечен нелинейный характер: линейный участок в области малых доз (до 0,1 Гр) и дозонезависимое плато в диапазоне доз от 1 до 5 Гр. Полученные данные позволяют использовать метод ДНК-комет для оценки биологического действия малых доз γ-излучения на проростки Allium cepa.

В работе польского ученого Гражины Быстшеевской-Пиотровской и Павла Урбана было охарактеризовано распределение 137Cs и 40K между слоями органа хранения съедобного лука. Во внутренних слоях колбы была обнаружена значительная корреляция (r = 0,96) между концентрациями цезия и калия. С другой стороны, соотношение 137Cs/40K в сухих старческих листьях было значительно увеличено. Поглощение цезия листьями и корнями (из 0,3 мм CsCl в буфере Tris –HCl при pH=7) исследовали в контролируемых условиях. В течение 48 часов происходил интенсивный акропетальный и базипетальный транспорт. В другом тесте саженцы лука инкубировали в 0,3 мм растворе CsCl в течение 24 ч. После переноса их в незагрязненную почву выращивали три группы лука в течение 4, 8 и 12 дней. Наблюдалось снижение содержания 137Cs в растениях через 8 и 12 дней, особенно в корнях, в то время как содержание 137Cs в листьях не изменилось. Лук в значительной степени накапливает цезий. Было показано, что Allium cepa поглощает цезий из осадков и является резервуаром 137Cs, из которого он выделяется в незагрязненную почву.

В исследовании Шикхи Чанделя и Шалиндера Каура изучалась роль излучения электромагнитного поля (EMF-r) сотового телефона в провоцировании окислительного повреждения корней лука (Allium cepa) на частоте 2100 МГц. Корни лука подвергали воздействию непрерывной волны однородного EMF-r в течение 1, 2 и 4 ч в течение одного дня и измеряли образование активных форм кислорода (АФК) в пересчете на содержание малонового диальдегида (MDA), перекиси водорода (H2O2) и супероксидного аниона (O2•−) и изменения активности антиоксидантных ферментов - супероксиддисмутазы (СОД) и каталазы (CAT). Результаты показали, что воздействие EMF-r увеличивает содержание MDA, H2O2 и O2•−. Кроме того, в корнях лука наблюдалось повышение активности антиоксидантных ферментов − SOD и CAT. В исследовании был сделан вывод о том, что EMF-r сотового телефона с частотой 2100 МГц вызывает окислительное повреждение корней лука, изменяя окислительный метаболизм.

Приложение 2
Описание методов статистической обработки данных.
t-критерий Стьюдента – общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. Он используется для определения статистической значимости различий средних величин. Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
где М1 - средняя арифметическая первой сравниваемой совокупности (группы), М2 - средняя арифметическая второй сравниваемой совокупности (группы), m1 - средняя ошибка первой средней арифметической, m2 - средняя ошибка второй средней арифметической.
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
f = (n1 + n2) - 2

Парный t-критерий Стьюдента – одна из модификаций метода Стьюдента, используемая для определения статистической значимости различий парных (повторных) измерений.
Парный t-критерий Стьюдента используется для сравнения двух зависимых (парных) выборок. Зависимыми являются измерения, выполненные у одних и тех же пациентов, но в разное время, например, артериальное давление у больных гипертонической болезнью до и после приема антигипертензивного препарата. Нулевая гипотеза гласит об отсутствии различий между сравниваемыми выборками, альтернативная - о наличии статистически значимых различий.

Парный t-критерий Стьюдента рассчитывается по следующей формуле:
где Мd - средняя арифметическая разностей показателей, измеренных до и после, σd - среднее квадратическое отклонение разностей показателей, n - число исследуемых.
Интерпретация полученного значения парного t-критерия Стьюдента не отличается от оценки t-критерия для несвязанных совокупностей. Прежде всего, необходимо найти число степеней свободы f по следующей формуле:
f = n - 1
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p<0,05) и при данном числе степеней свободы f.

U-критерий Манна-Уитни – непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.

Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд, путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.
В составленном едином ранжированном ряду общее количество рангов получится равным N = n1 + n2 где n1 - количество элементов в первой выборке, а n2 - количество элементов во второй выборке.
Вновь разделяем единый ранжированный ряд на два, состоящие соответственно из единиц первой и второй выборок, запоминая при этом значения рангов для каждой единицы. Подсчитываем отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно - на долю элементов второй выборки. Определяем большую из двух ранговых сумм (Tx) соответствующую выборке с nx элементами.
Находим значение U-критерия Манна-Уитни по формуле:
Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) с критическим значением U при заданной численности сопоставляемых выборок.

Критерий Уилкоксона для связанных выборок (Т-критерий Уилкоксона) – непараметрический статистический критерий, используемый для сравнения двух связанных (парных) выборок по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.
Суть метода состоит в том, что сопоставляются абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
Т-критерий Уилкоксона используется для оценки различий между двумя рядами измерений, выполненных для одной и той же совокупности исследуемых, но в разных условиях или в разное время. Данный тест способен выявить направленность и выраженность изменений - то есть, являются ли показатели больше сдвинутыми в одном направлении, чем в другом.

Как рассчитать Т-критерий Уилкоксона для связанных выборок?
Вычислить разность между значениями парных измерений для каждого исследуемого. Нулевые сдвиги далее не учитываются.
Определить, какие из разностей являются типичными, то есть соответствуют преобладающему по частоте направлению изменения показателя.
Проранжировать разности пар по их абсолютным значениям (то есть, без учета знака), в порядке возрастания. Меньшему абсолютному значению разности приписывается меньший ранг.
Рассчитать сумму рангов, соответствующих нетипичным сдвигам.
Таким образом, Т-критерий Уилкоксона для связанных выборок рассчитывается по следующей формуле: T = ΣRr где ΣRr - сумма рангов, соответствующих нетипичным изменениям показателя.
Полученное значение T-критерия Уилкоксона сравниваем с критическим по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) при заданной численности сопоставляемых выборок n:
Если расчетное (эмпирическое) значение Тэмп. меньше табличного Ткр. или равно ему, то признается статистическая значимость изменений показателя в типичную сторону (принимается альтернативная гипотеза). Достоверность различий тем выше, чем меньше значение Т.
Если Тэмп. больше Ткр., принимается нулевая гипотеза об отсутствии статистической значимости изменений показателя.

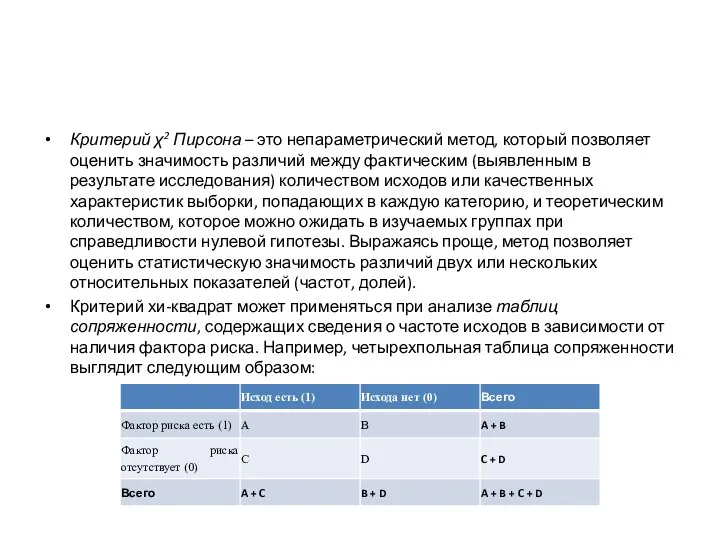
Критерий χ2 Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
Критерий хи-квадрат может применяться при анализе таблиц сопряженности, содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженности выглядит следующим образом:

Приложение 2
Пример описания данных на основе полученных первичных результатов исследования: статья Лебединского, Лаврского и Четанова «Влияние частоты электромагнитного излучения дециметрового диапазона на процесс митоза в растительных тканях»

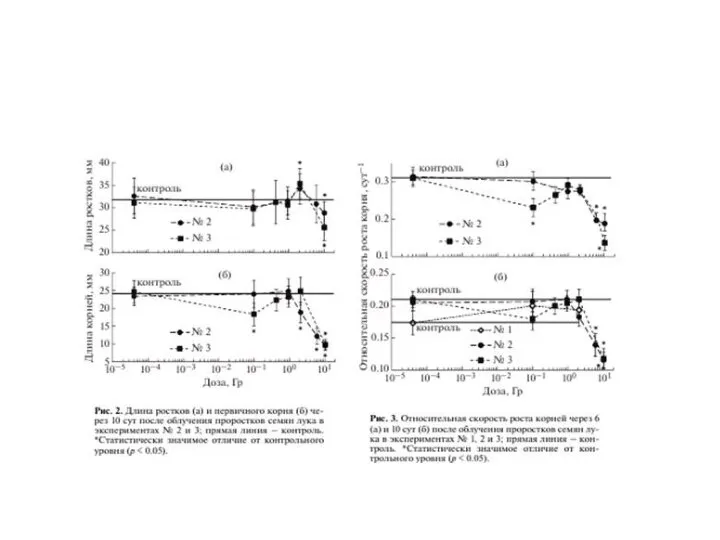
Статья Трофимовой, Дементьева и Болсуновского «Влияние γ-излучения на развитие растений из облученных семян и проростков Allium cepa L.»

Приложение 3
РАДИОЧУВСТВИТЕЛЬНОСТЬ ВОДОРОСЛЕВЫХ КУЛЬТУР SCENEDESMUS QUADRICAUDA, ВЫДЕЛЕННЫХ ИЗ РАДИОАКТИВНО ЗАГРЯЗНЕННЫХ ВОДОЕМОВ ПО «МАЯК»
Тема этого исследования крайне актуальна, так как в настоящее время развиваются атомные технологии, серьезно воздействующие на биосферу, следовательно, необходимо исследование тех организмов, которые могут служить биоиндикаторами радиационного загрязнения. При изучении водных экосистем нужно уделить внимание водорослевым сообществам (с целью определения безопасных уровней воздействия радиационного излучения) и изучить закономерности реакции водных экосистем на неблагоприятные факторы.
Изменения в структуре альгоценоза, вызванные, например, радиационным воздействием спровоцируют определенные реакции в других элементах водной экосистемы.