Содержание
- 2. План лекції Поняття стійкість Математичні умови стійкості Критерій стійкості Гурвіца.
- 3. 1. Поняття стійкість Незбуреним рухом САУ називають рух ідеальної (безінерційної) системи під впливом заданого зовнішнього сигналу.
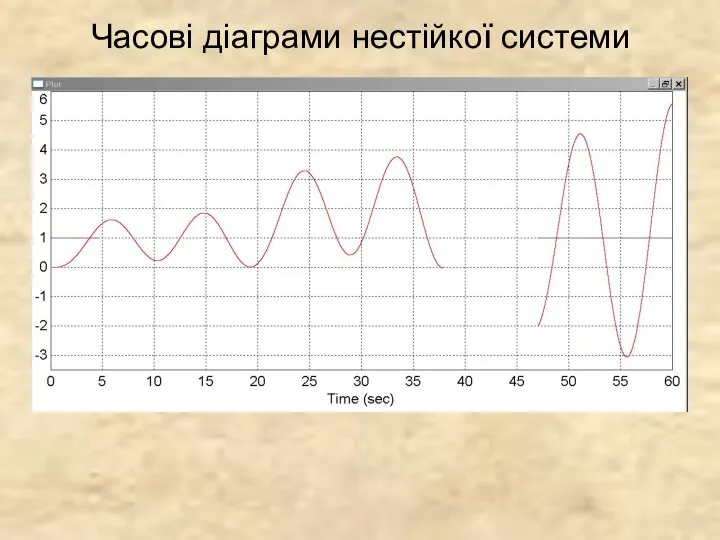
- 4. Часові діаграми нестійкої системи
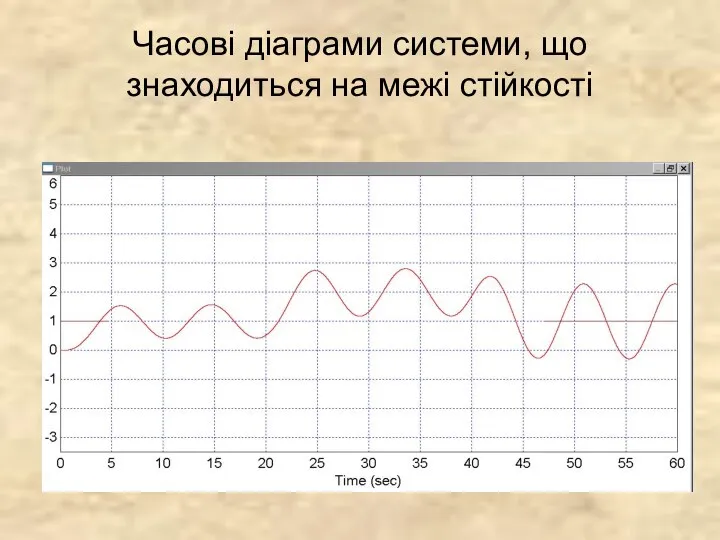
- 5. Часові діаграми системи, що знаходиться на межі стійкості
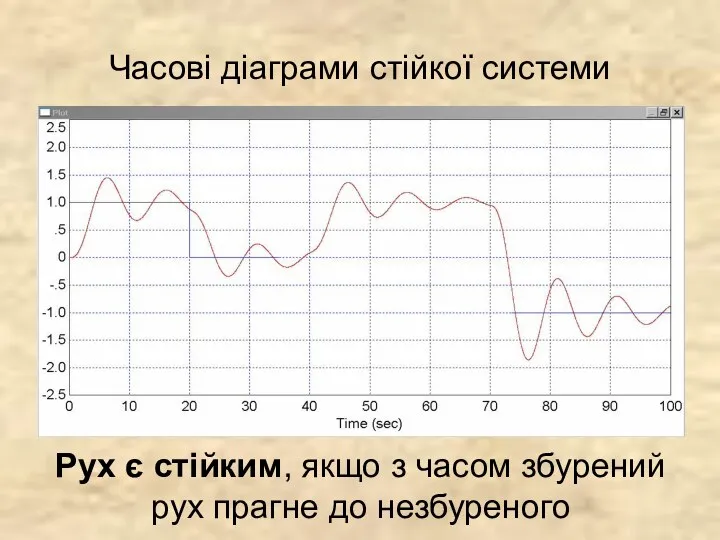
- 6. Часові діаграми стійкої системи Рух є стійким, якщо з часом збурений рух прагне до незбуреного
- 7. Ляпунов, Александр Михайлович (25 мая (6 июня) 1857, Ярославль — 3 ноября 1918, Одесса) — русский
- 8. 2. Математичні умови стійкості Рішення рівняння, що відповідає збуреному руху: Для того, щоб система була стійкою,
- 9. Рішення однорідного рівняння може бути отримано у вигляді: λ i - корені характеристичного рівняння : Для
- 10. Необхідна і достатня ознака стійкості лінійного об'єкту полягає в тому, щоб усі корені характеристичного рівняння мали
- 11. 3. Алгебраїчний критерій Гурвіца Критерій стійкості – це умови, виконання яких необхідно і достатньо, щоб усі
- 12. Адольф Гурвиц (нем. Adolf Hurwitz), 26 березня 1859, Хильдесхайм — 18 листопада 1919, Цюрих) — немецкий
- 13. Якщо всі корені алгебраїчного рівняння: розташовані зліва, т.т. мають від’ємну дійсну частину, якщо коефіцієнти i всі
- 14. Визначник Гурвіца:
- 15. Визначники Гурвіца для системи 4-го порядку: Визначники Гурвіца для системи 3-го порядку:
- 17. Скачать презентацию











 Презентация на тему Устный счёт 1 класс
Презентация на тему Устный счёт 1 класс  Фундаментальные и прикладные исследования в метрологии
Фундаментальные и прикладные исследования в метрологии Проценты. Определение, обозначение, вычисление, применение Математика 5 класс
Проценты. Определение, обозначение, вычисление, применение Математика 5 класс Логарифмическая спираль
Логарифмическая спираль Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Вычитание числа 7
Вычитание числа 7 Свойства числовых неравенств. 8 класс
Свойства числовых неравенств. 8 класс Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Обыкновенные дроби
Обыкновенные дроби Обыкновенные дроби
Обыкновенные дроби parallelnost_1
parallelnost_1 Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве 2._3
2._3 Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования
Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования Теория о трех перпендикулярах
Теория о трех перпендикулярах Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Задачи на части
Задачи на части Вероятность события
Вероятность события Цифра в 21 веке
Цифра в 21 веке Решение неравенств
Решение неравенств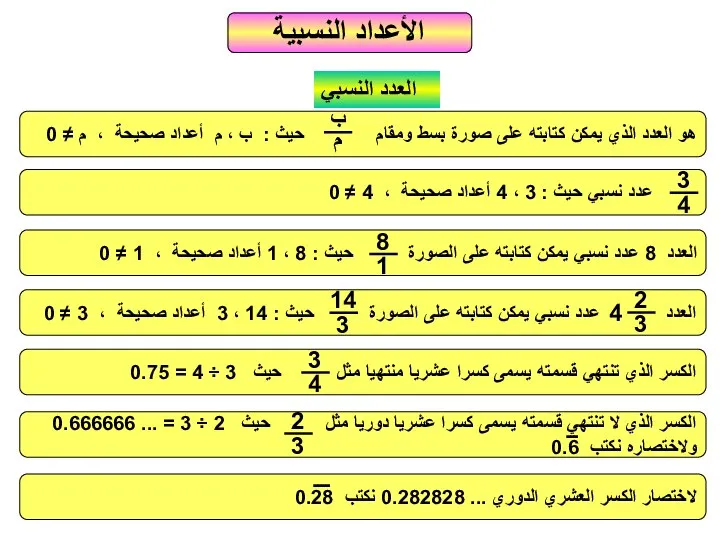 األعداد النسبية العدد النسبي ب
األعداد النسبية العدد النسبي ب Движение по окружности
Движение по окружности Математические структуры
Математические структуры Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи
Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи Игра
Игра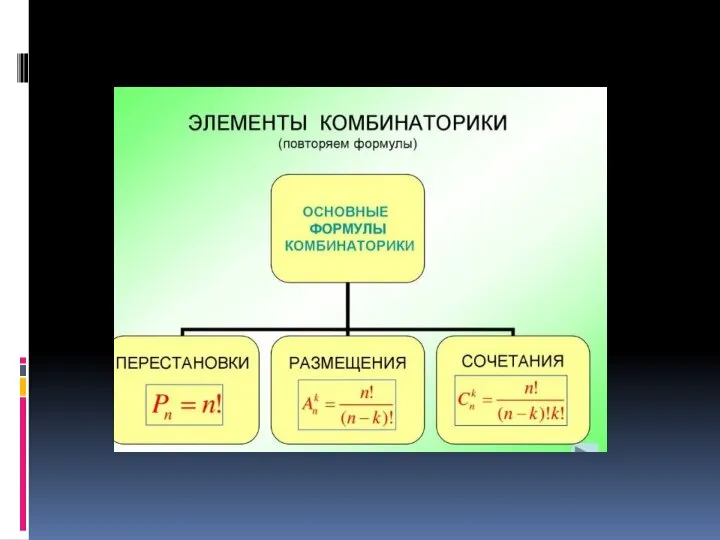 Основные понятия комбинаторики
Основные понятия комбинаторики Косинус угла
Косинус угла