Содержание
- 2. Сегодня на уроке
- 3. В науке и на практике часто встречаются задачи, решая которые, возникает необходимость составлять различные комбинации из
- 4. Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем
- 5. Правило произведения
- 7. Приписав к каждому из этих чисел любую из имеющихся пяти цифр, мы получим различные трёхзначные числа.
- 9. Правило произведения Правило произведения может быть применено неоднократно для подсчёта числа соединений из трёх, четырёх, пяти
- 10. Задание № 1 Решение: Число всевозможных двузначных чисел, составленных с помощью предложенных четырёх цифр:
- 11. Задание № 2 Решение:
- 12. Задание № 3 Решение: В качестве второй цифры может быть записана любая из оставшихся трёх цифр.
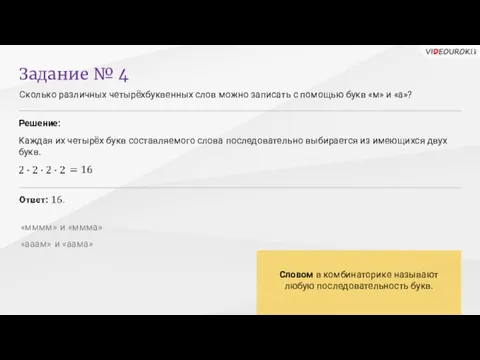
- 13. Сколько различных четырёхбуквенных слов можно записать с помощью букв «м» и «а»? Задание № 4 Решение:
- 14. Задание № 5 Решение:
- 15. Сколькими способами можно составить расписание шести уроков на один день из шести различных учебных предметов? Задание
- 16. Сколько различных поездов можно составить из девяти вагонов, если каждый из вагонов можно поставить на любом
- 17. Задание № 8 Решение: На должность старосты можно выбрать одного из двадцати учеников. На должность физорга
- 18. Задание № 9 Решение:
- 20. Скачать презентацию
















 Планиметрия. Решение прямоугольного треугольника
Планиметрия. Решение прямоугольного треугольника Short end волатильность. Значение для управления нелинейной позицией. Обзор основных идей анализа
Short end волатильность. Значение для управления нелинейной позицией. Обзор основных идей анализа Применение производной в физике
Применение производной в физике Показательные уравнения
Показательные уравнения Параллельные прямые
Параллельные прямые Разряды и классы. Чтение и запись многозначных чисел (4 класс)
Разряды и классы. Чтение и запись многозначных чисел (4 класс) Граф – набор точек, некоторые из которых соединены линиями
Граф – набор точек, некоторые из которых соединены линиями Различные виды уравнений
Различные виды уравнений praktika_3
praktika_3 Задачи на построение
Задачи на построение Формулы двойного аргумента
Формулы двойного аргумента Деление с остатком. 4 класс
Деление с остатком. 4 класс Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс)
Презентация на тему Письменный приём умножения многозначного числа на двузначное (4 класс) 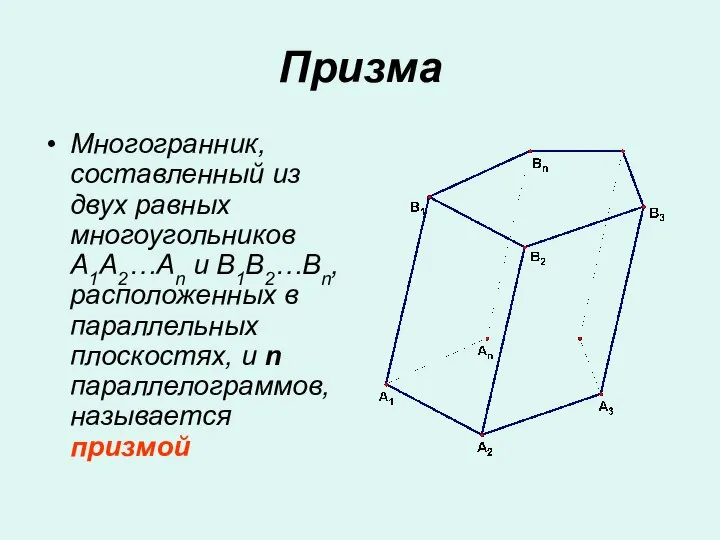 Призма. Боковые ребра призмы
Призма. Боковые ребра призмы Многочлен и его стандартный вид
Многочлен и его стандартный вид Принцип относительности Галилея
Принцип относительности Галилея Бой эрудитов
Бой эрудитов Исследовательская работа Загадки треугольника. 9 класс
Исследовательская работа Загадки треугольника. 9 класс Основные тригонометрические тождества. Преобразование тригонометрических выражений
Основные тригонометрические тождества. Преобразование тригонометрических выражений Функция y = ax^2, её график и свойства
Функция y = ax^2, её график и свойства Величины, длина
Величины, длина Таблица умножения на 3
Таблица умножения на 3 Решение квадратных уравнений по формуле
Решение квадратных уравнений по формуле Объёмные и плоские предметы. 1 класс
Объёмные и плоские предметы. 1 класс Признаки равенства треугольников
Признаки равенства треугольников Решение задач. Вариант 9
Решение задач. Вариант 9 Треугольники. Основные определения
Треугольники. Основные определения Дивергентные математические задачи как средство развития креативности мышления у младших школьников
Дивергентные математические задачи как средство развития креативности мышления у младших школьников