Устойчивость движения, классификация точек покоя,

Рассмотрим нелинейную систему дифференциальных уравнений, запишем ее уравнения в векторной форме
Или в координатной форме
.
В качестве независимой переменной выбрано время t, поэтому система дифференциальных уравнений является моделью некоторого процесса – изменения переменной во времени или Движения материальной точки, Занимающей в фазовом пространстве текущее положение и изменяющей это положение с изменением времени t. Таким образом, Движение – это частное решение системы дифференциальных уравнений.

Зададим некоторые начальные условия . Пусть выполняются условия теоремы Коши (непрерывны в рассматриваемой области). Тогда через любую точку расширенного фазового пространства из рассматриваемой области проходит единственная интегральная кривая – график частного решения . Назовем движение, «начинающееся» в точке Невозмущенным движением . Если «возмутить» – несколько изменить начальные условия в фазовом пространстве, выбрать их , то изменится и движение. Назовем движение,«начинающееся» в точке , Возмущенным движением . Если возмущение начальных условий невелико, то в некоторой окрестности начальной точки траектории – движения тоже близки.

Рассматривая близость возмущенного и невозмущенного движений «вообще», при любом времени t > T, мы приходим к определению Устойчивости движения по Ляпунову.
Движение называется Устойчивым по Ляпунову, Если
определения в том, что для любого размера окрестности «допуска» (по фазовым координатам) невозмущенного движения существует размер окрестности, в которой можно «возмутить» начальные условия. Причем это возмущение приведет к тому, что возмущенное движение после некоторого момента времени Т войдет в окрестность «допуска» и останется в этой окрестности при любом t > T.

Если движение устойчиво по Ляпунову и , то такое движение называется Асимптотически устойчивым.
Если движение асимптотически устойчиво, то возмущенное движение с ростом времени стремится к невозмущенному.
Движение называется Неустойчивым по Ляпунову, если
Смысл этого определения в том, что как бы ни было мало возмущение начальных условий, все равно со временем хотя бы по одной координате возмущенное движение выйдет из некоторой окрестности «допуска» невозмущенного движения.

Теорема. Задача об устойчивости движения может быть сведена к задаче об устойчивости тривиального (тождественно равного нулю) решения системы.
Доказательство. Обозначим . Тогда
При Имеем , поэтому задача об устойчивости движения для исходной системы уравнений может быть заменена эквивалентной ей задачей об устойчивости тривиального решения для системы
.
Поэтому обычно заранее делают указанную замену и исследуют задачу об устойчивости тривиального решения.

Устойчивость по первому приближению.
Будем рассматривать автономную систему
И ее «систему первого приближения»
Заметим, что систему первого приближения можно строить, линеаризуя в окрестности нуля элементы матрицы, заменяя бесконечно малые элементы матрицы эквивалентными.

КЛАССИФИКАЦИЯ ТОЧЕК ПОКОЯ ДЛЯ АВТОНОМНЫХ СИСТЕМ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ.
СИСТЕМА ВТОРОГО ПОРЯДКА.
Запишем уравнение автономной системы второго порядка
Точка покоя
1. Корни характеристического уравнения действительны..

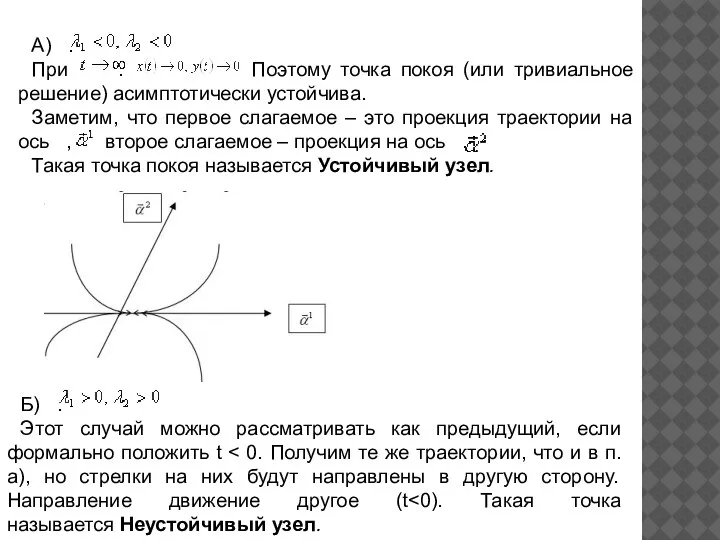
А) .
При . Поэтому точка покоя (или тривиальное решение) асимптотически устойчива.
Заметим, что первое слагаемое – это проекция траектории на ось , второе слагаемое – проекция на ось .
Такая точка покоя называется Устойчивый узел.
Б) .
Этот случай можно рассматривать как предыдущий, если формально положить t < 0. Получим те же траектории, что и в п. а), но стрелки на них будут направлены в другую сторону. Направление движение другое (t<0). Такая точка называется Неустойчивый узел.

В) .
По вектору мы, находясь на траектории, стремимся к нулю, по вектору , наоборот, удаляемся от нуля.
Такая точка покоя - Седло.
Г) .
Это – тоже седло, но стрелки
Направлены в другую сторону.
Траектория прижимается к той оси, для которой модуль характеристического числа меньше.
Седла – неустойчивые точки покоя.
Заметим, в ситуациях узлов и седла траектория, начавшись в определенном квадранте, в нем и остается.

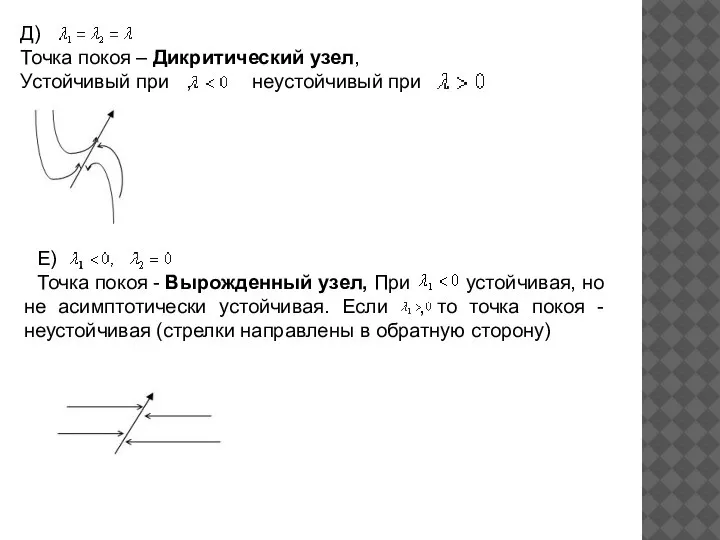
Д) .
Точка покоя – Дикритический узел,
Устойчивый при , неустойчивый при
Е)
Точка покоя - Вырожденный узел, При устойчивая, но не асимптотически устойчивая. Если , то точка покоя - неустойчивая (стрелки направлены в обратную сторону)

Ж) . Точка безразличного равновесия. При изменении времени любая точка остается на месте. Этими точками заполнена вся плоскость.
2. Корни характеристического уравнения комплексно сопряженные.
Параметр t имеет смысл угла поворота вокруг начала координат (в периодической составляющей).

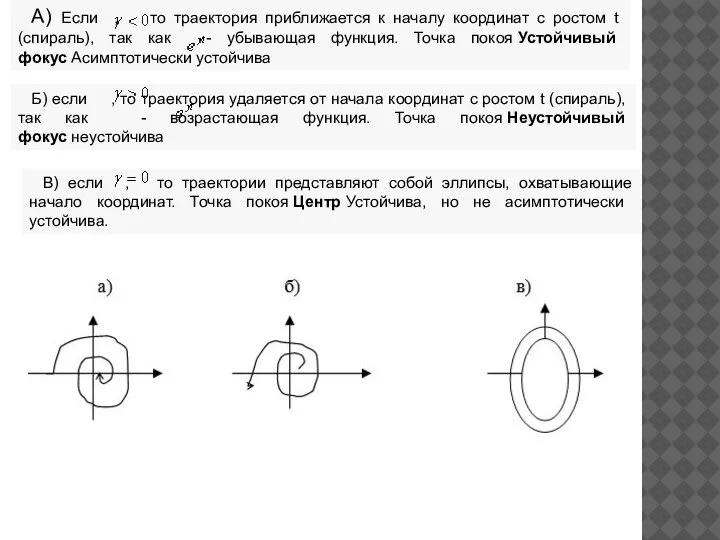
А) Если , то траектория приближается к началу координат с ростом t (спираль), так как - убывающая функция. Точка покоя Устойчивый фокус Асимптотически устойчива
Б) если , то траектория удаляется от начала координат с ростом t (спираль), так как - возрастающая функция. Точка покоя Неустойчивый фокус неустойчива
В) если , то траектории представляют собой эллипсы, охватывающие начало координат. Точка покоя Центр Устойчива, но не асимптотически устойчива.

Система третьего порядка.
Запишем уравнение автономной системы третьего порядка
1) Все корни характеристического уравнения действительны и различны.
Картину поведения фазовых траекторий довольно легко представить, рассматривая поведение фазовых траекторий в плоскостях, натянутых на пары собственных векторов. Этот случай уже изучен выше.

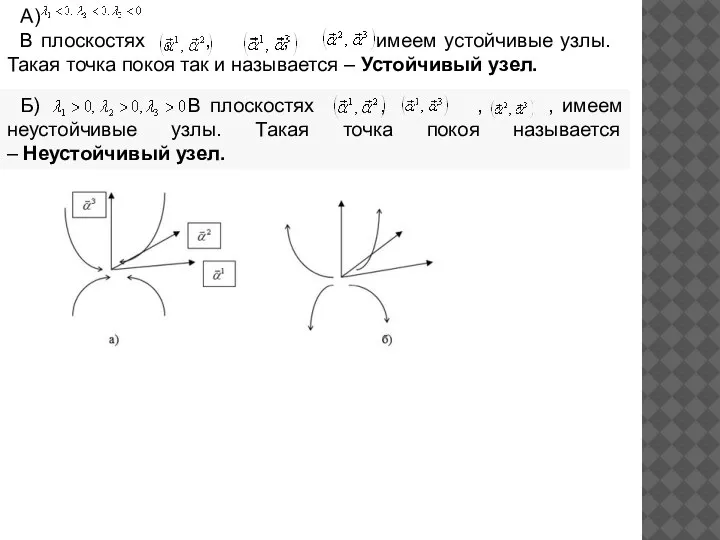
А)
В плоскостях , , , имеем устойчивые узлы. Такая точка покоя так и называется – Устойчивый узел.
Б) В плоскостях , , , имеем неустойчивые узлы. Такая точка покоя называется – Неустойчивый узел.

В) один корень имеет знак, противоположный остальным двум корням. Точка покоя в этом случае называется Седло – узел И является неустойчивой точкой покоя.
Пусть, например, . Тогда в плоскости имеем неустойчивый узел, а в плоскостях , - седла. Если , то в плоскости имеем устойчивый узел, а в плоскостях , - седла.
Заметим, что в ситуациях узлов и седла – узел траектория, начавшись в определенном октанте, не переходит в другой октант.
2) - действительный корень характеристического уравнения, - комплексно сопряженная пара корней.

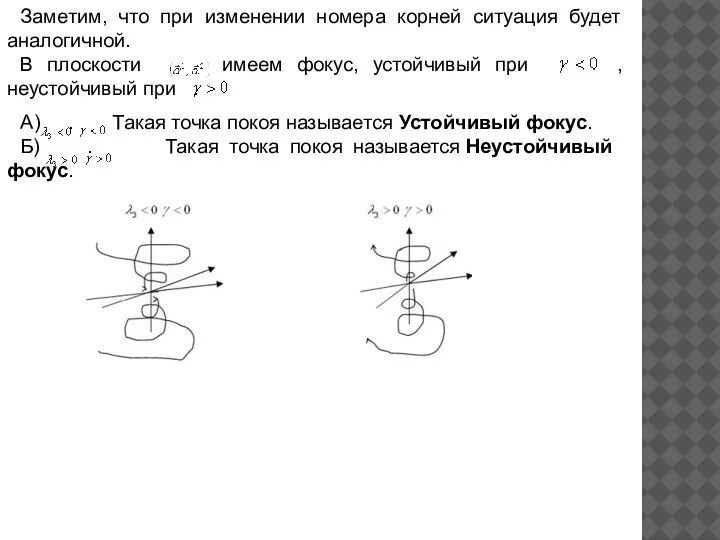
Заметим, что при изменении номера корней ситуация будет аналогичной.
В плоскости имеем фокус, устойчивый при , неустойчивый при .
А) . Такая точка покоя называется Устойчивый фокус.
Б) . Такая точка покоя называется Неустойчивый фокус.