Содержание
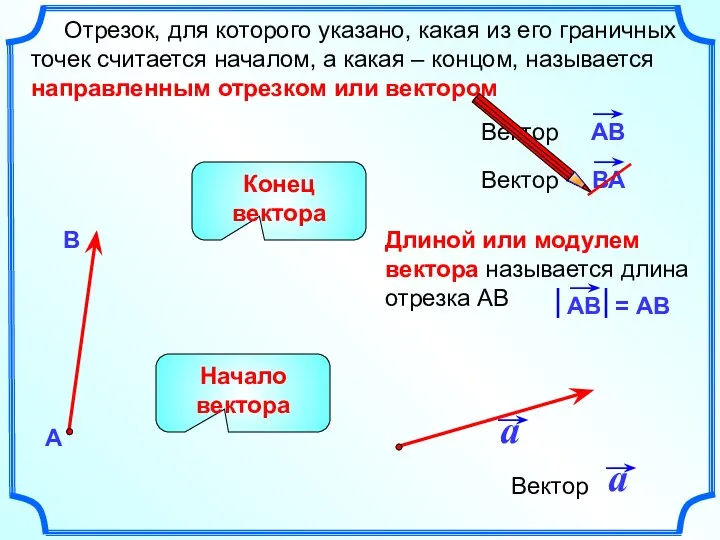
- 2. Длиной или модулем вектора называется длина отрезка АВ Отрезок, для которого указано, какая из его граничных
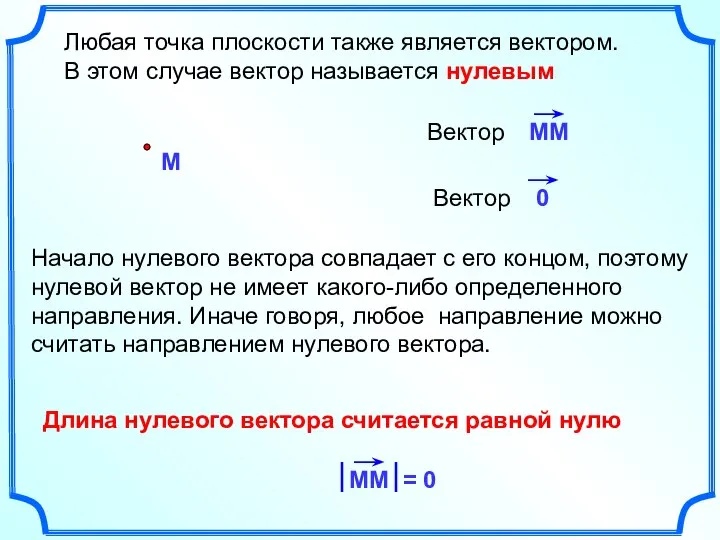
- 3. Любая точка плоскости также является вектором. В этом случае вектор называется нулевым Длина нулевого вектора считается
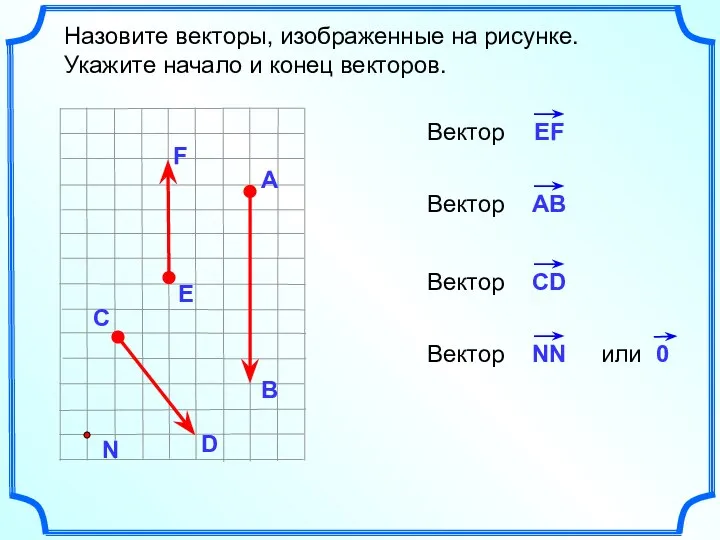
- 4. Назовите векторы, изображенные на рисунке. Укажите начало и конец векторов.
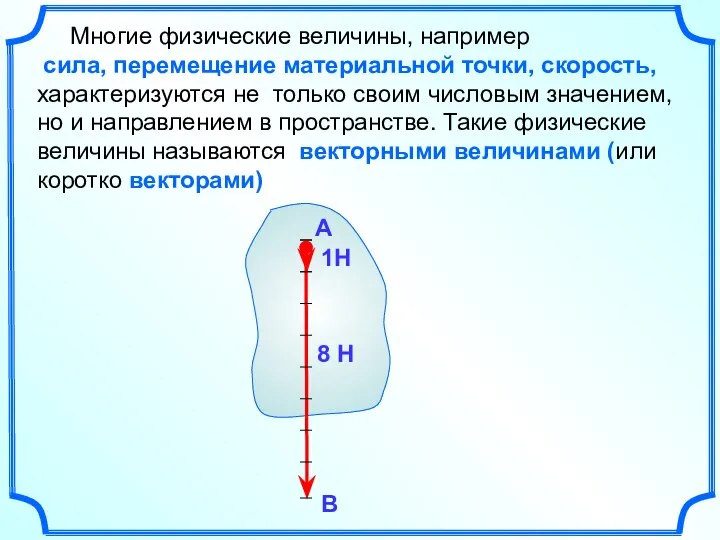
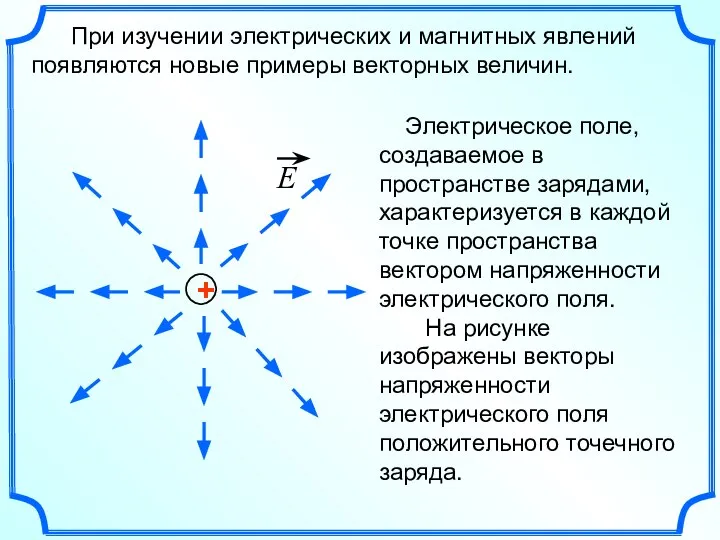
- 5. Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но
- 6. При изучении электрических и магнитных явлений появляются новые примеры векторных величин.
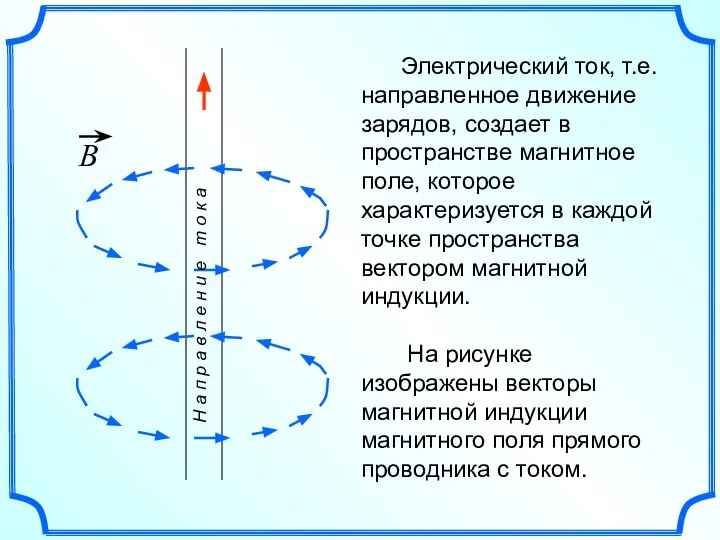
- 7. Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке
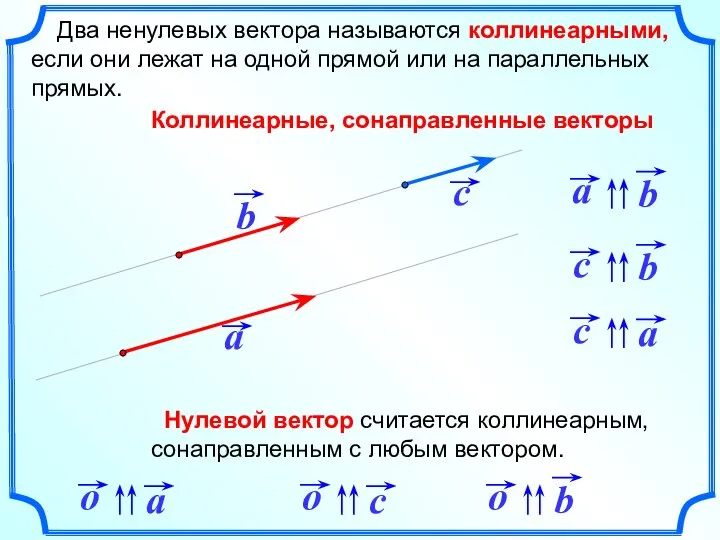
- 8. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные,
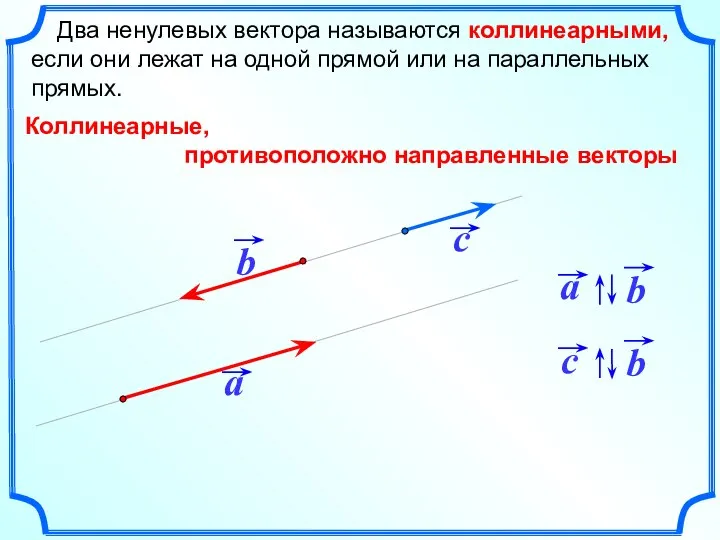
- 9. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные,
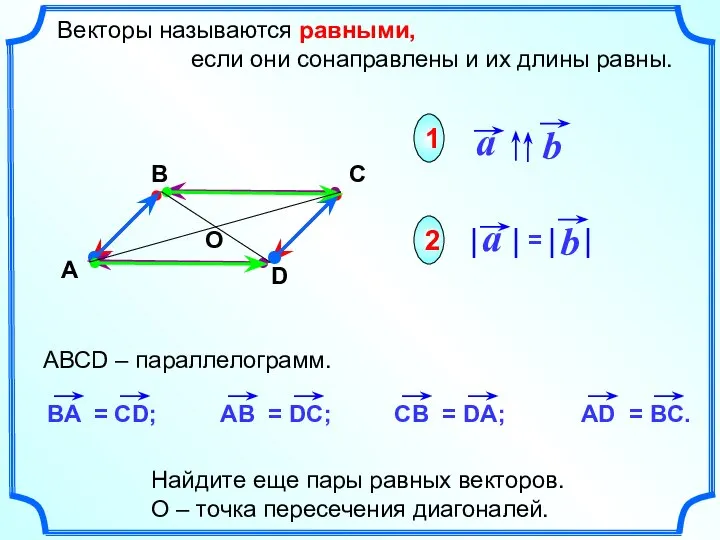
- 10. Векторы называются равными, если они сонаправлены и их длины равны. 1 2 Найдите еще пары равных
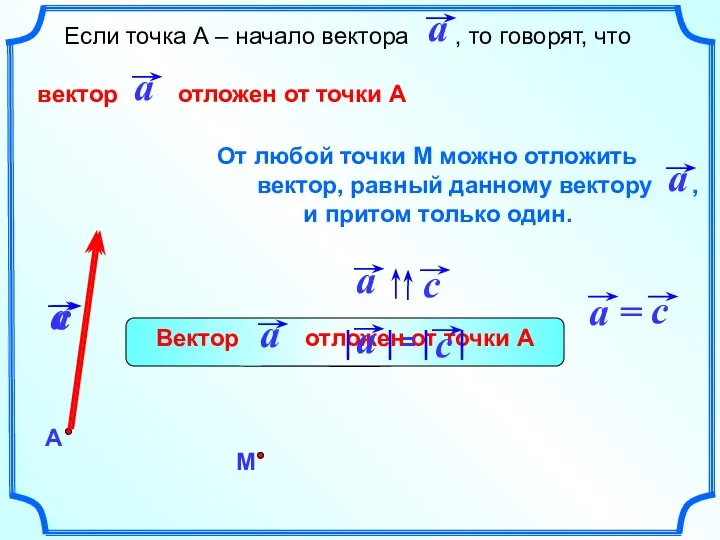
- 11. Если точка А – начало вектора , то говорят, что вектор отложен от точки А
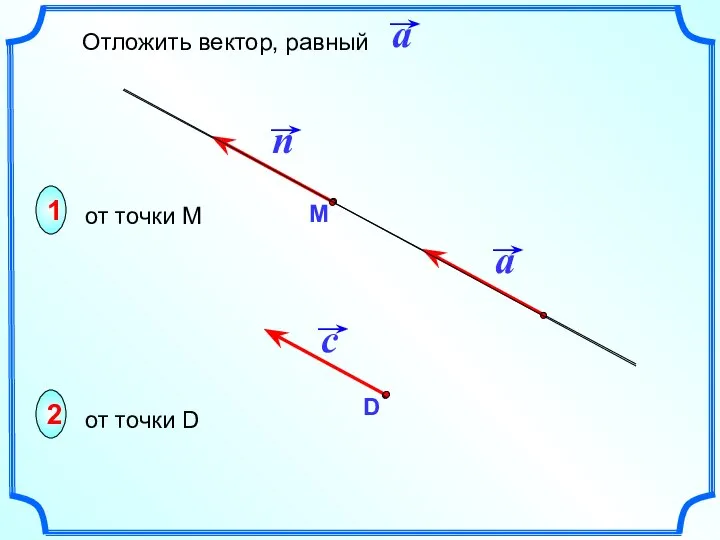
- 12. 1 2 от точки М от точки D
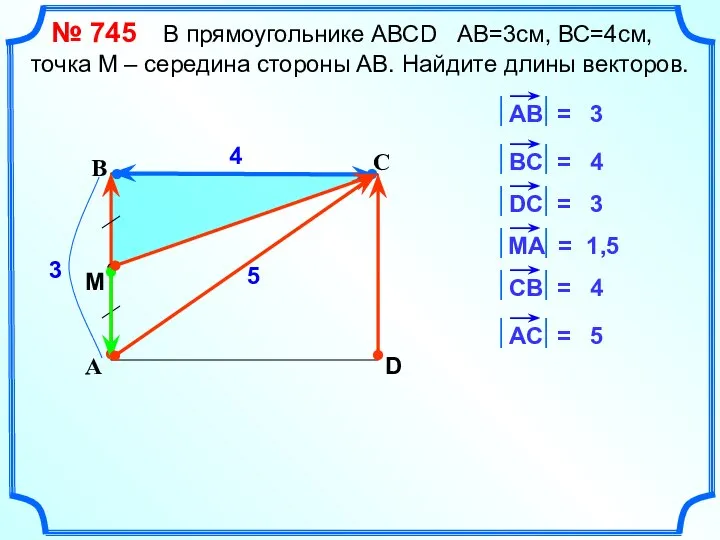
- 13. С А В D 4 3 4 3 1,5 4 5 5 M № 745 В
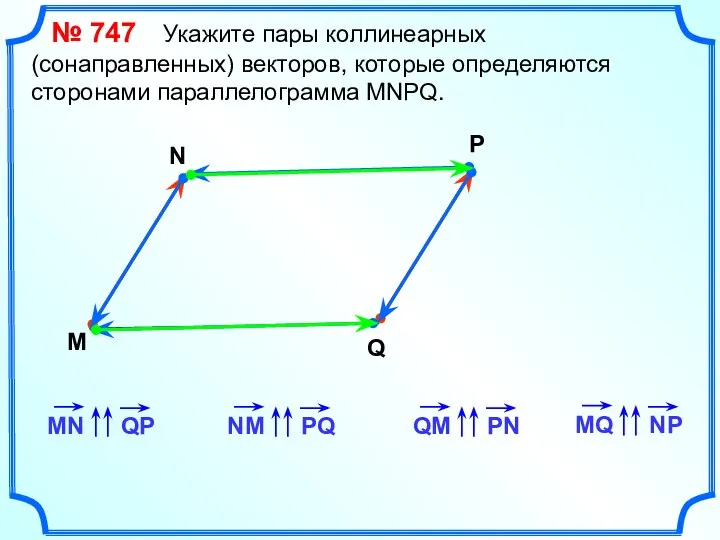
- 14. № 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами параллелограмма MNPQ. M N P Q
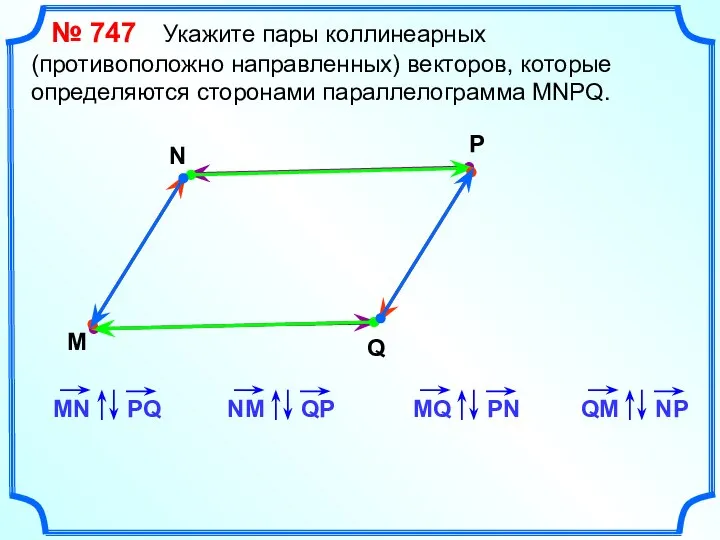
- 15. № 747 Укажите пары коллинеарных (противоположно направленных) векторов, которые определяются сторонами параллелограмма MNPQ. M N P
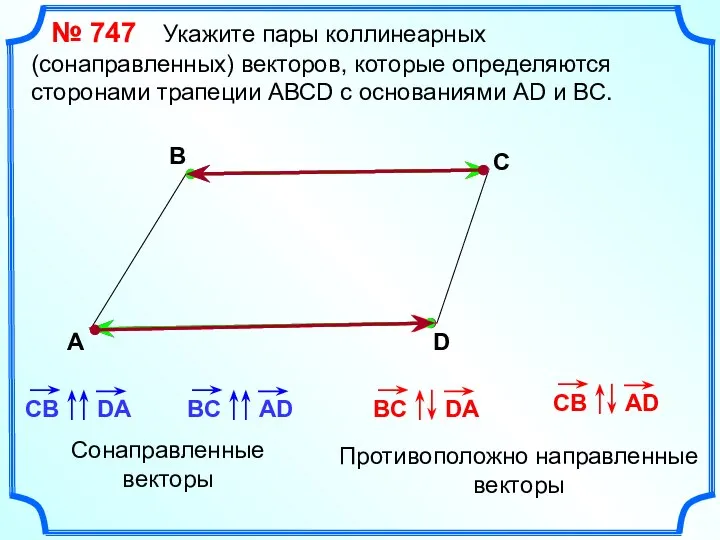
- 16. № 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами трапеции АВСD с основаниями AD и
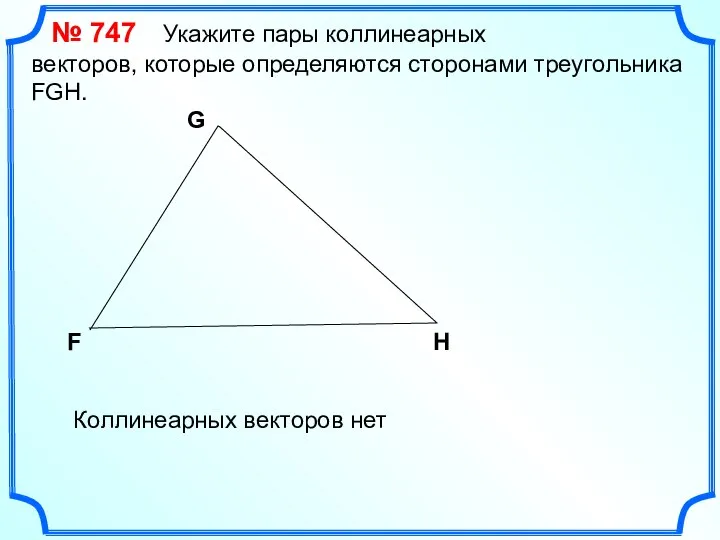
- 17. № 747 Укажите пары коллинеарных векторов, которые определяются сторонами треугольника FGH. F G H Коллинеарных векторов
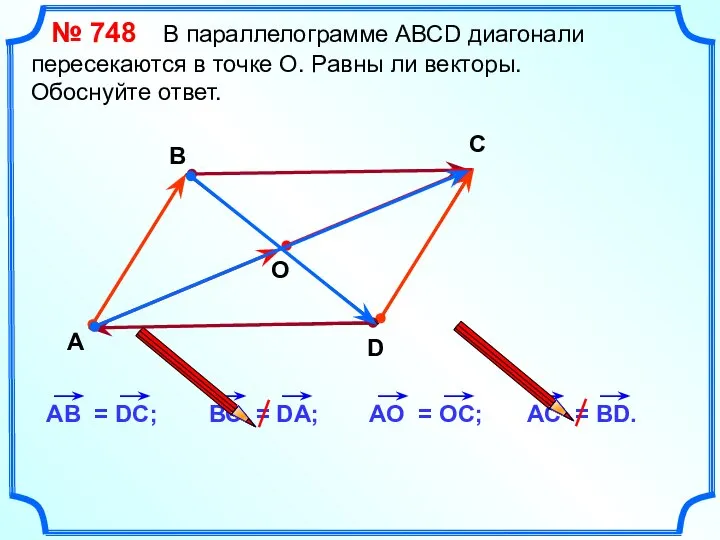
- 18. № 748 В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы. Обоснуйте ответ. А
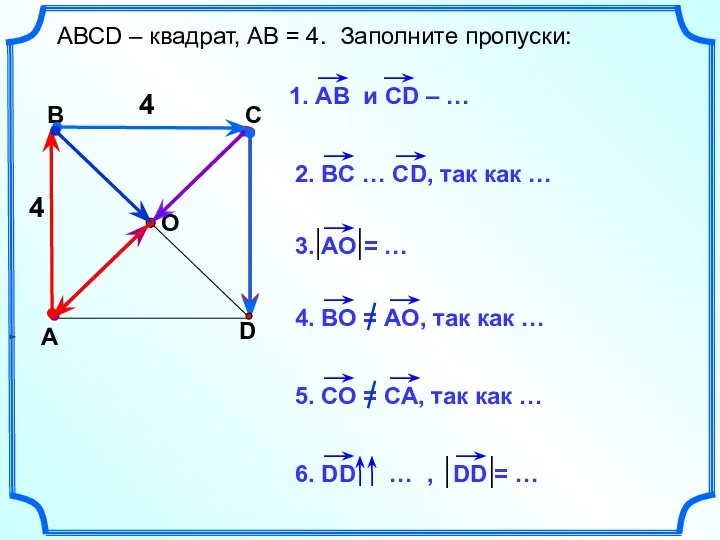
- 19. АВСD – квадрат, АВ = 4. Заполните пропуски: 4 4
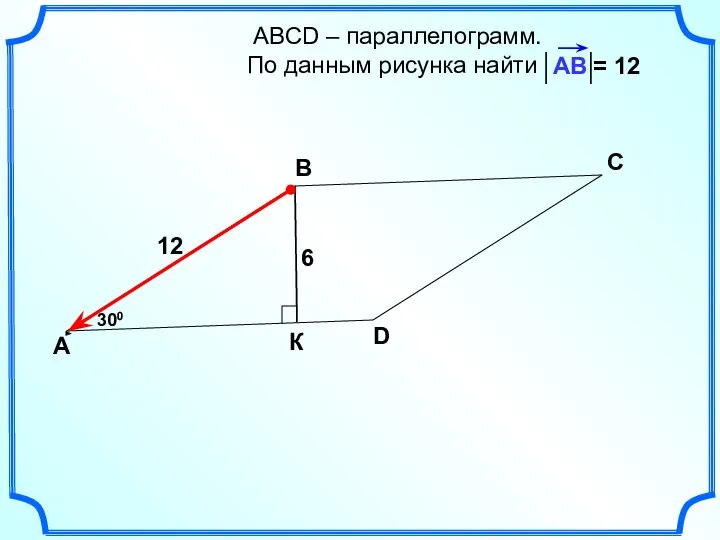
- 20. АВСD – параллелограмм. По данным рисунка найти А В С D 300 6 К 12 =
- 22. Скачать презентацию
 Движение и виды движения
Движение и виды движения 5_vektory
5_vektory Степень с целым показателем. Блиц-опрос
Степень с целым показателем. Блиц-опрос Классические алгоритмы на графах
Классические алгоритмы на графах Несложная тригонометрия
Несложная тригонометрия Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Логарифмические уравнения и методы их решения
Логарифмические уравнения и методы их решения Решение задач. Повторение пройденного
Решение задач. Повторение пройденного Золотое сечение
Золотое сечение Системы с цилиндрическим фазовым пространством
Системы с цилиндрическим фазовым пространством Таблица сложения
Таблица сложения Сумма углов в треугольнике
Сумма углов в треугольнике Метрология: применение математической статистики при измерениях и испытаниях
Метрология: применение математической статистики при измерениях и испытаниях Сечение тетраэдра
Сечение тетраэдра Математика. Занятие Число 7
Математика. Занятие Число 7 Решение задачи дуффинга регуляризованными методами неполного прогноза
Решение задачи дуффинга регуляризованными методами неполного прогноза Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений
Статистические характеристики: среднее арифметическое, мода, медиана называются средними результатами измерений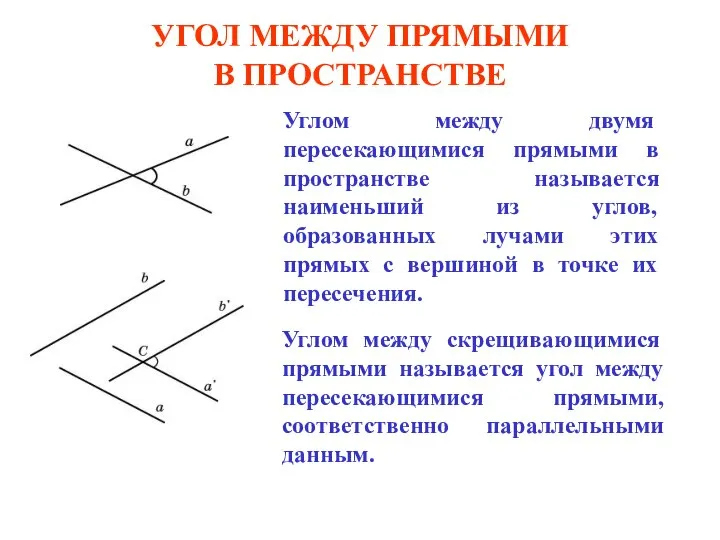 Угол между двумя прямыми в пространстве Вариант 2.ppt
Угол между двумя прямыми в пространстве Вариант 2.ppt Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Арифметический корень степени n
Арифметический корень степени n Обыкновенные дроби
Обыкновенные дроби Производная сложной функции
Производная сложной функции Симплекс метод. Лекция 5
Симплекс метод. Лекция 5 Свойства равнобедренных треугольников
Свойства равнобедренных треугольников Прикладной количественный анализ заголовков
Прикладной количественный анализ заголовков Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Математическая викторина. 1 тур. Занимательные задачи
Математическая викторина. 1 тур. Занимательные задачи Решение системы уравнений первой степени с двумя неизвестными
Решение системы уравнений первой степени с двумя неизвестными