Содержание
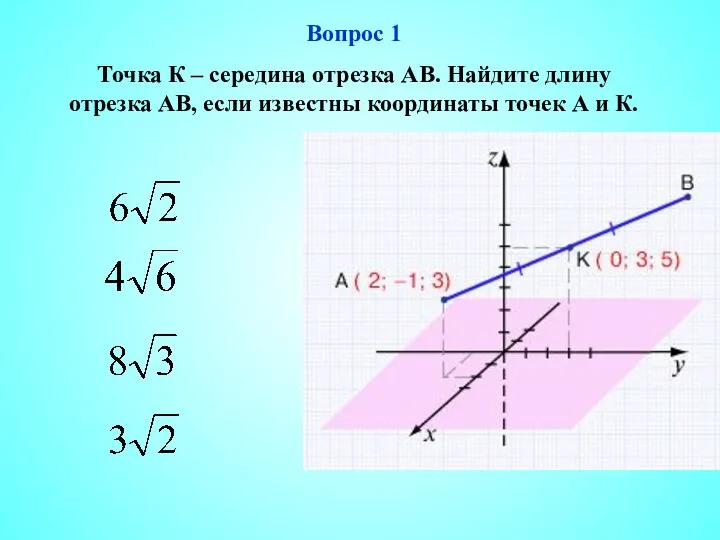
- 2. Вопрос 1 Точка К – середина отрезка АВ. Найдите длину отрезка АВ, если известны координаты точек
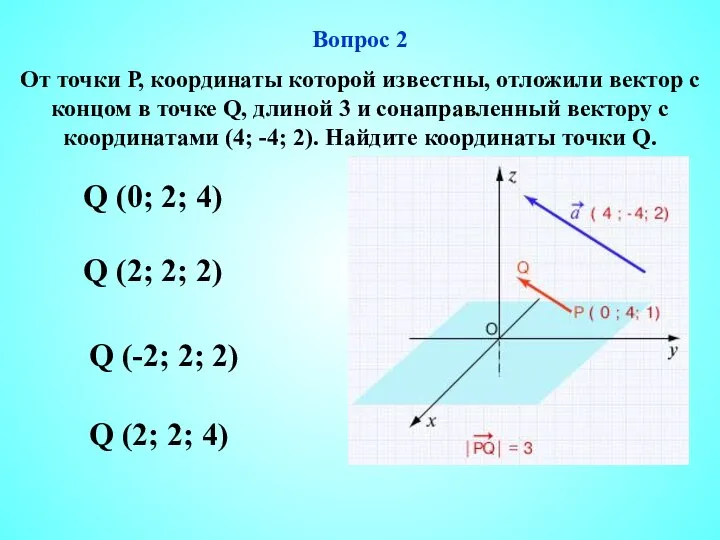
- 3. Вопрос 2 От точки Р, координаты которой известны, отложили вектор с концом в точке Q, длиной
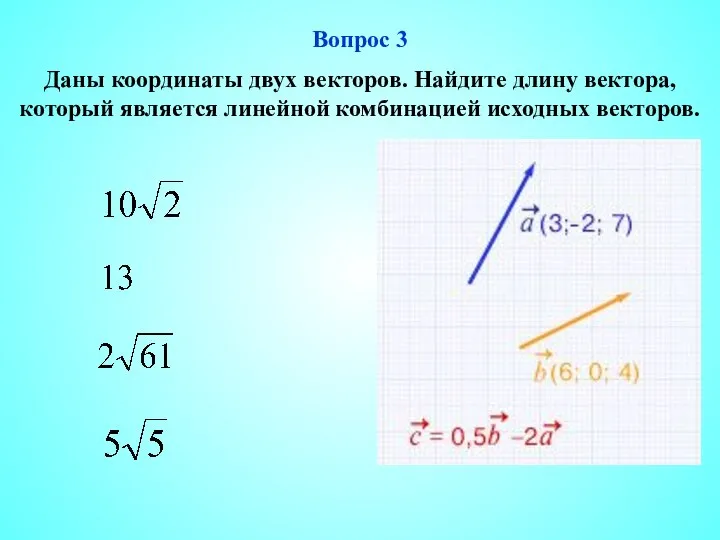
- 4. Вопрос 3 Даны координаты двух векторов. Найдите длину вектора, который является линейной комбинацией исходных векторов.
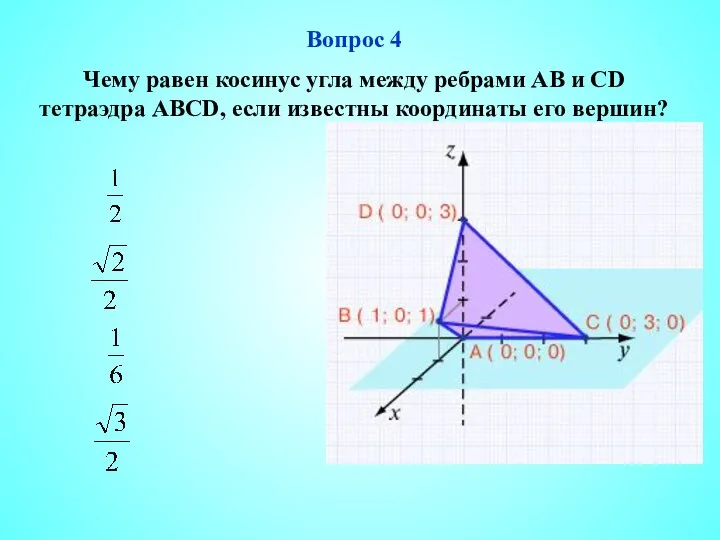
- 5. Вопрос 4 Чему равен косинус угла между ребрами АВ и СD тетраэдра ABCD, если известны координаты
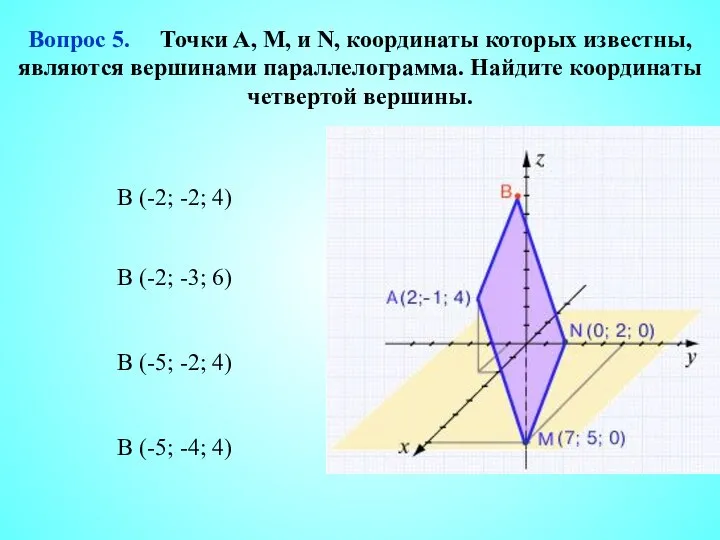
- 6. B (-5; -4; 4) B (-2; -3; 6) B (-5; -2; 4) B (-2; -2; 4)
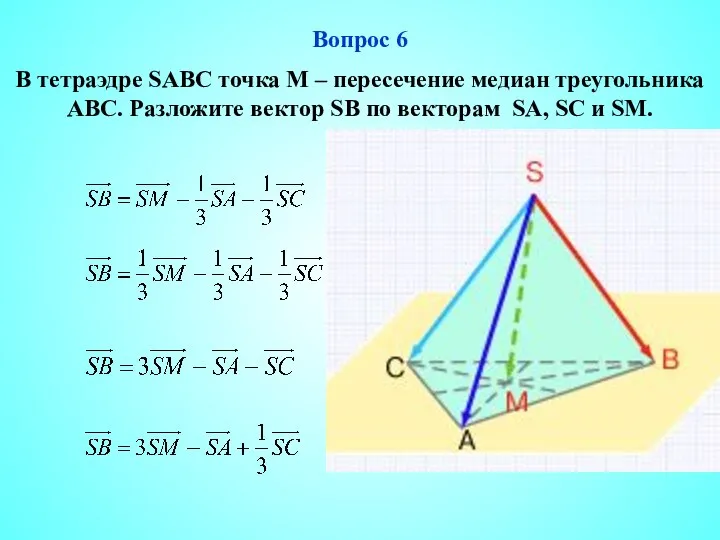
- 7. Вопрос 6 В тетраэдре SABC точка М – пересечение медиан треугольника АВС. Разложите вектор SB по
- 8. 2x + 5y + 3z – 4 = 0 2x – 5y – 3z – 9
- 10. Скачать презентацию

 Сходимость последовательности СВ
Сходимость последовательности СВ Цепочка бусин
Цепочка бусин Сложение смешанных чисел
Сложение смешанных чисел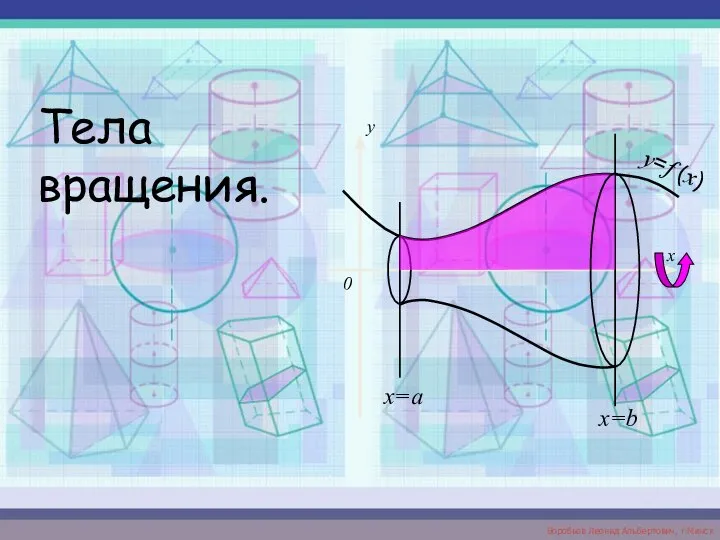 Тела вращения
Тела вращения Логарифмические уравнения
Логарифмические уравнения Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Периметр
Периметр Презентация на тему Смежные углы
Презентация на тему Смежные углы  Прямоугольный треугольник. Тренажер. 8 класс
Прямоугольный треугольник. Тренажер. 8 класс Уравнение и его корни
Уравнение и его корни Понятие функции. Свойства функций
Понятие функции. Свойства функций “Збери” задачу
“Збери” задачу Теорія ймовірностей, ймовірнісні процеси і математична статистика
Теорія ймовірностей, ймовірнісні процеси і математична статистика Решение уравнений. Устная работа
Решение уравнений. Устная работа Решение задач на многогранники, цилиндр, конус, шар
Решение задач на многогранники, цилиндр, конус, шар Умножение числа 2 и на 2
Умножение числа 2 и на 2 Презентация на тему ИСПОЛЬЗОВАНИЕ МЕТОДИКИ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ НА УРОКАХ МАТЕМАТИКИ
Презентация на тему ИСПОЛЬЗОВАНИЕ МЕТОДИКИ РАЗВИВАЮЩЕГО ОБУЧЕНИЯ НА УРОКАХ МАТЕМАТИКИ  Пропорциональные величины
Пропорциональные величины Конструктор (2)
Конструктор (2) قدرمطلقی درجه اول
قدرمطلقی درجه اول Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта
Математический тренажёр. Устные упражнения на уроках математики в 7 классе как один из способов отработки навыка устного счёта Презентация на тему Понятие функции (7 класс)
Презентация на тему Понятие функции (7 класс)  Способы решения уравнений. Методика профессионального обучения
Способы решения уравнений. Методика профессионального обучения Угол между высотой и биссектрисой. Применение тригонометрии в геометрических задачах
Угол между высотой и биссектрисой. Применение тригонометрии в геометрических задачах Строительство бакалавриата. Приложения производной
Строительство бакалавриата. Приложения производной Понятие математической индукции и ее применение
Понятие математической индукции и ее применение Решение простейших тригонометрических уравнений с помощью числовой окружности
Решение простейших тригонометрических уравнений с помощью числовой окружности Уголок математики в подготовительной группе
Уголок математики в подготовительной группе