Содержание
- 2. При обучении геометрических фигур, кривых на уроках математики преподавателю необходимо создать у учеников правильные геометрические образы,
- 3. Знакомство с кривыми и изучение их свойств углубит знания, геометрические представления, повысит интерес к геометрии; создаст
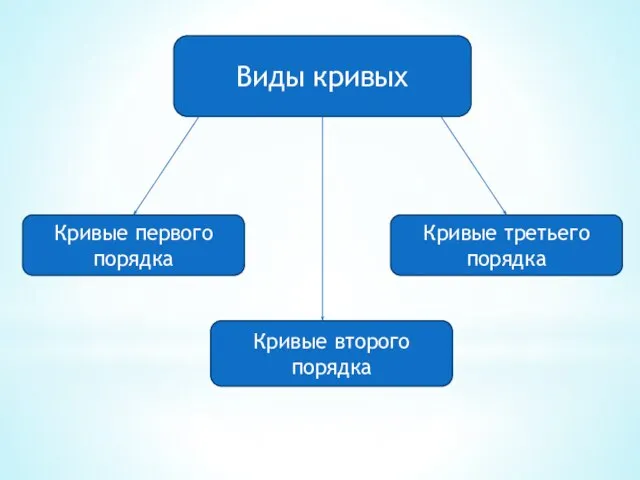
- 4. Виды кривых Кривые первого порядка Кривые второго порядка Кривые третьего порядка
- 5. Кривые первого порядка Линия первого порядка на плоскости определяется алгебраическим уравнением первой степени относительно декартовых координат
- 6. Кривые второго порядка Кривой второго порядка называется линия, уравнение которой в декартовой системе координат имеет вид:
- 7. Кривыми второго порядка могут быть: окружность; эллипс; гипербола; парабола; - их вырождения.
- 8. Окружность. Окружностью называется геометрическое место точек M(x, y) плоскости, расстояние которых до данной точки A(a, b)
- 9. Эллипс Эллипсом называется геометрическое место точек M(x, y) плоскости, сумма расстояний которых до двух данных точек
- 10. Гипербола Гиперболой называется геометрическое место точек M(x, y) плоскости, разность расстояний которых до двух данных точек
- 11. Парабола Параболой называется геометрическое место точек M(x, y) плоскости, равноотстоящих от данной точки F этой плоскости
- 12. Кривые третьего порядка Примером кривой третьего порядка рассмотрим строфоиду. Алгебраическая кривая в Евклидовой плоскости называется циркулярной,
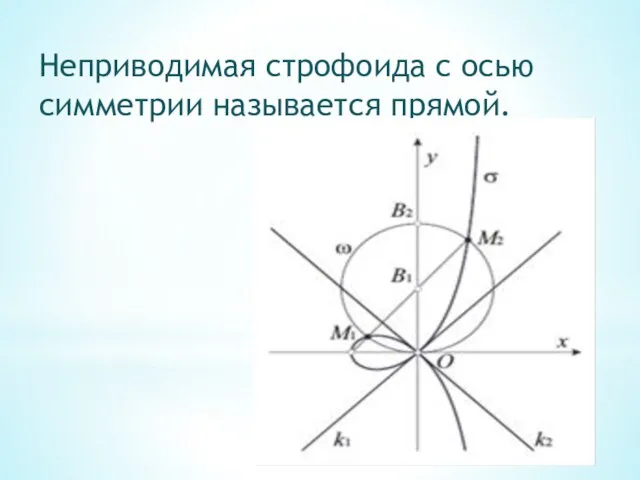
- 13. Неприводимая строфоида с осью симметрии называется прямой.
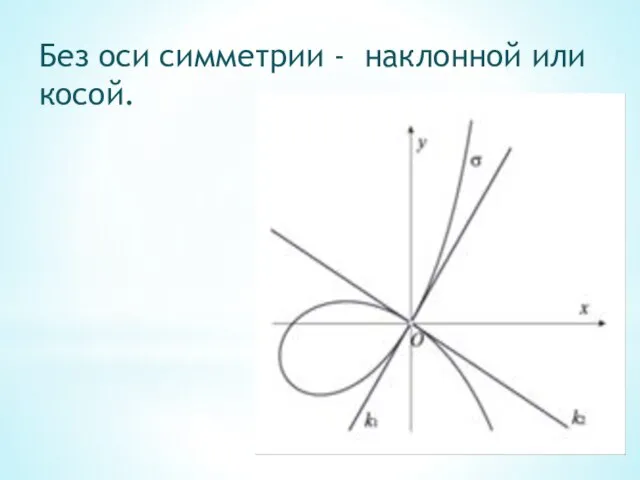
- 14. Без оси симметрии - наклонной или косой.
- 15. Примеры задач из учебника Н.Б. Истоминой и М.И.Моро. Примеры из учебников Н.Б. Истомина и М.И. Моро
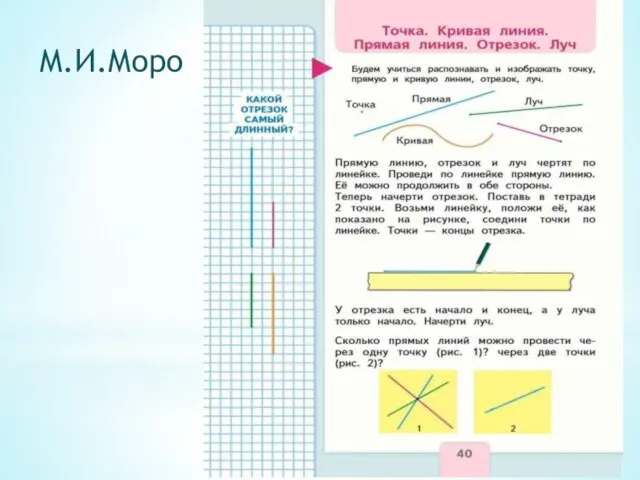
- 16. М.И.Моро
- 17. М.И.Моро
- 18. М.И.Моро
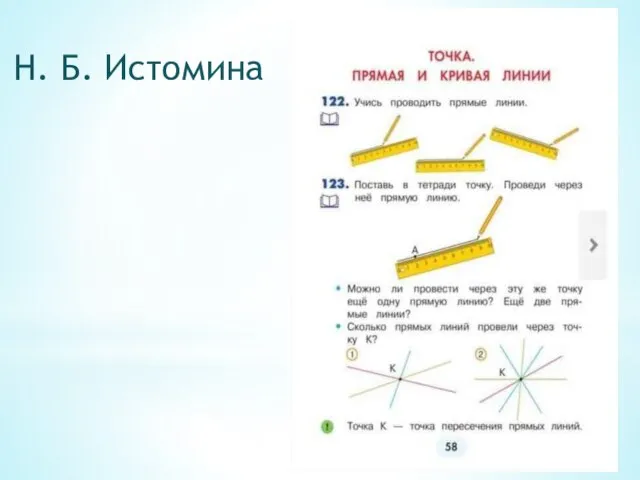
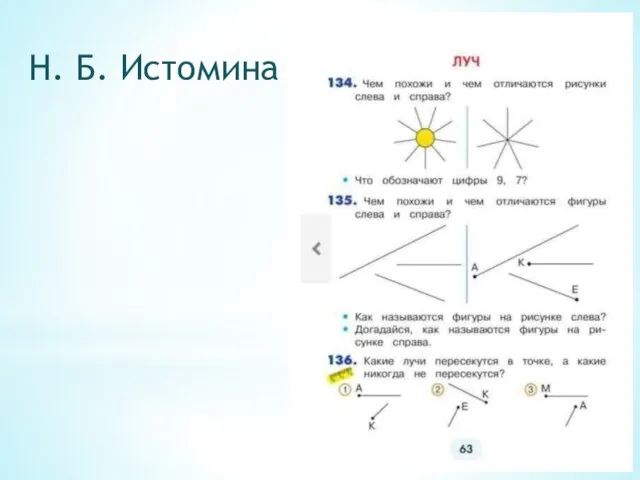
- 19. Н. Б. Истомина
- 20. Н. Б. Истомина
- 21. Н. Б. Истомина
- 22. ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ Часто мы не замечаем, что в жизни нас окружает множество кривых. Мы встречаем их
- 23. Кривой Жордана называется образ непрерывного инъективного отображения окружности или отрезка в пространство. В случае окружности кривая
- 24. Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.
- 25. Кривой Урысона называется связное компактное топологическое пространство Cтопологической размерности 1.
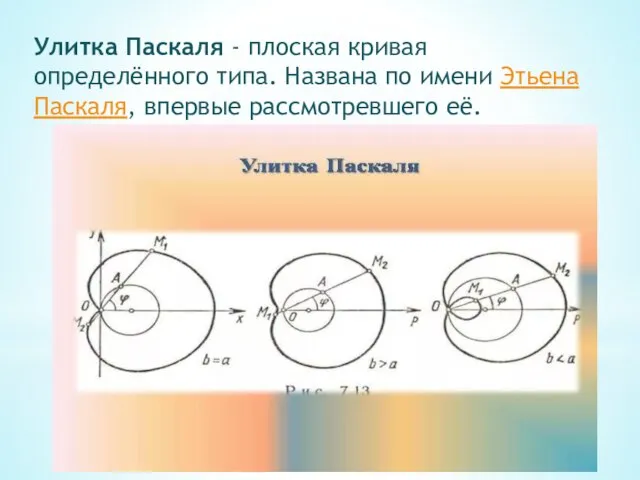
- 26. Улитка Паскаля - плоская кривая определённого типа. Названа по имени Этьена Паскаля, впервые рассмотревшего её.
- 27. Роза Гранди Как-то раз итальянский геометр Гвидо Гранди(1671-1742) создал розы. Розы радуют глаз правильными и плавными
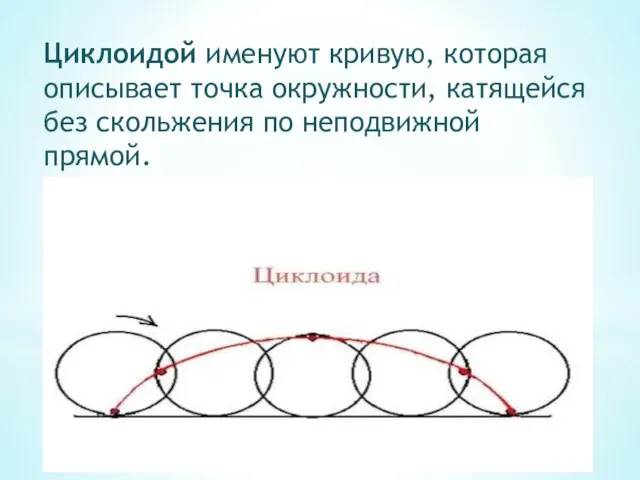
- 28. Циклоидой именуют кривую, которая описывает точка окружности, катящейся без скольжения по неподвижной прямой.
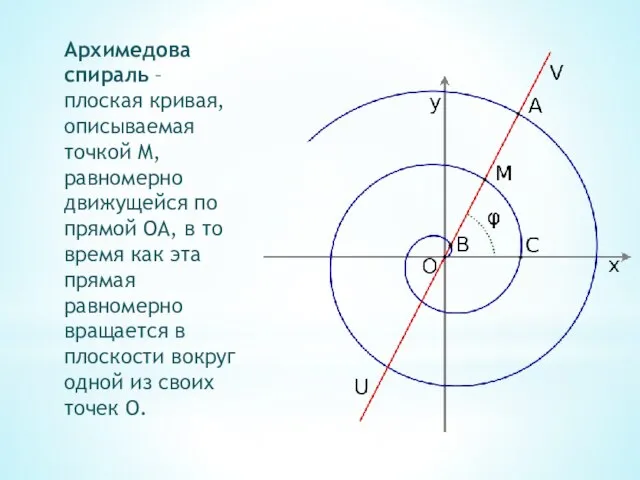
- 29. Архимедова спираль – плоская кривая, описываемая точкой M, равномерно движущейся по прямой OA, в то время
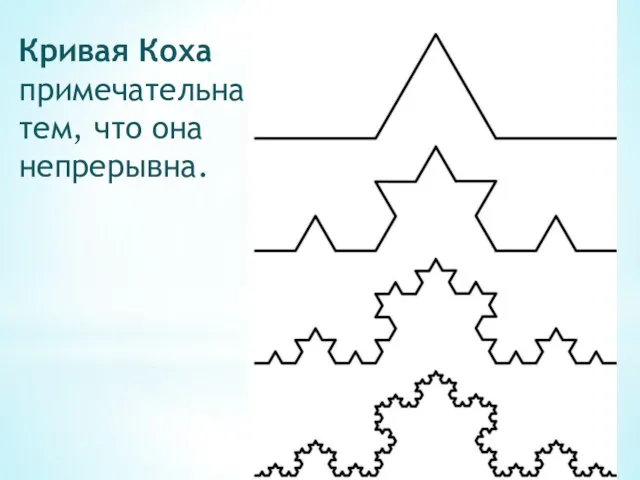
- 30. Кривая Коха примечательна тем, что она непрерывна.
- 31. ОКРУЖНОСТЬ И КРУГ Окружность - это замкнутая плоская кривая, которая состоит из всех точек на плоскости,
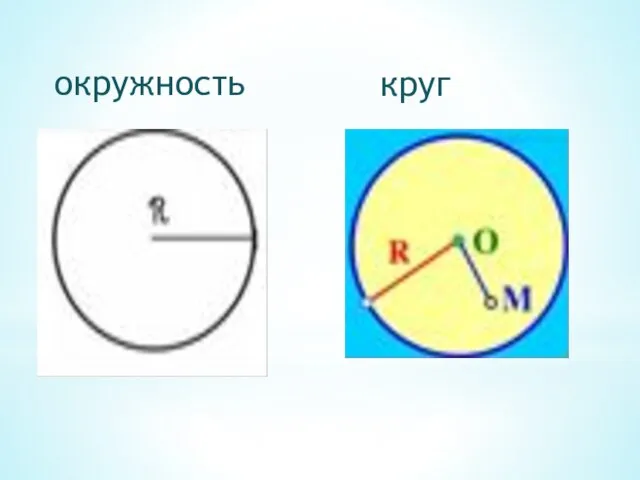
- 32. окружность круг
- 33. УМК «Школа России» М. И. Моро, С. И. Волкова, С. В. Степанова, М. А. Бантова, Г.
- 34. Ученики должны научиться: узнавать круг и окружность; знать, что окружность — это линия, являющаяся границей круга;
- 35. 3 класс 1 часть Тема урока: «Круг.Окружность»
- 36. Образовательные задачи урока: -Сформировать первоначальные представления об окружности и ее элементах (центр, радиус, диаметр); -познакомить с
- 37. «Доли» Раздел, в котором проходит изучение темы « Круг. Окружность» - «Доли». Назовите, какие доли круга
- 42. Это - окружность ОКРУЖНОСТЬ – замкнутая линия, все точки которой равноудалены от точки О (центра окружности).
- 43. Это - круг О Круг – часть плоскости, ограниченная окружностью.
- 44. Учимся строить окружность!
- 45. Алгоритм
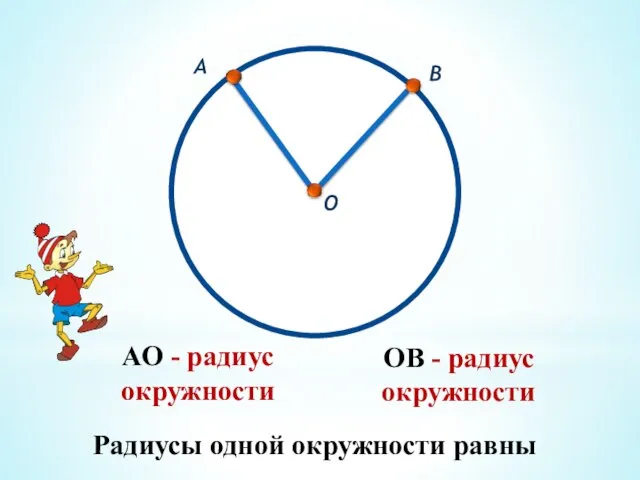
- 46. АО - радиус окружности О А ОВ - радиус окружности В Радиусы одной окружности равны
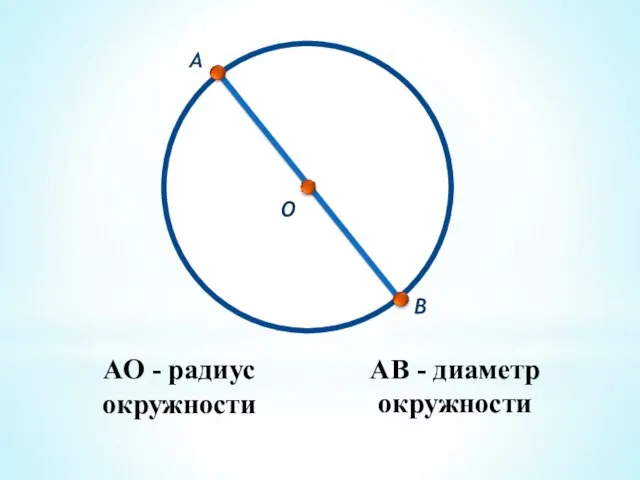
- 47. ДИАМЕТР (от греч. поперечник) - отрезок, соединяющий две точки окружности и проходящий через центр. Посмотрите на
- 48. АО - радиус окружности О А АВ - диаметр окружности В
- 49. Очень важное значение при усвоении понятий окружность и круг имеют задания, направленные на воспроизведение знаний и
- 50. Итог Как итог можно добавить, что работа по формированию навыков должна проводится постепенно почти на каждом
- 52. Скачать презентацию




































 Умножение дробей
Умножение дробей Совокупность математических методов для изучения свойств кубика Рубика
Совокупность математических методов для изучения свойств кубика Рубика Цифра 10
Цифра 10 Построение таблиц истинности
Построение таблиц истинности Презентация на тему Графическое решение квадратных уравнений (8 класс)
Презентация на тему Графическое решение квадратных уравнений (8 класс)  Медианы, биссектрисы и высоты треугольника. 7 класс
Медианы, биссектрисы и высоты треугольника. 7 класс Интегрированный урок (алгебра + физика). Действия со степенями 8 класс
Интегрированный урок (алгебра + физика). Действия со степенями 8 класс Интервальные вычисления. Лекция 11
Интервальные вычисления. Лекция 11 Презентация на тему Деление (2 класс)
Презентация на тему Деление (2 класс)  Экологическое воспитание через урок математики Учитель начальных классов Зайцева Вероника Петровна
Экологическое воспитание через урок математики Учитель начальных классов Зайцева Вероника Петровна Линейные уравнения с одной переменной, содержащие переменную под знаком модуля
Линейные уравнения с одной переменной, содержащие переменную под знаком модуля Определение функции
Определение функции Случаи сложения вида +5
Случаи сложения вида +5 Задания по математике для 3 класса
Задания по математике для 3 класса Великие математики
Великие математики Арифметическая прогрессия
Арифметическая прогрессия Занимательные задачи на смекалку
Занимательные задачи на смекалку Пифагория. Геометрия в клетках. Геймификация обучения
Пифагория. Геометрия в клетках. Геймификация обучения Нахождение числа по его дроби
Нахождение числа по его дроби Старинные рычажные безмены
Старинные рычажные безмены Решение неравенств с помощью систем
Решение неравенств с помощью систем определение и свойства числ.функции
определение и свойства числ.функции Ускоренное умножение
Ускоренное умножение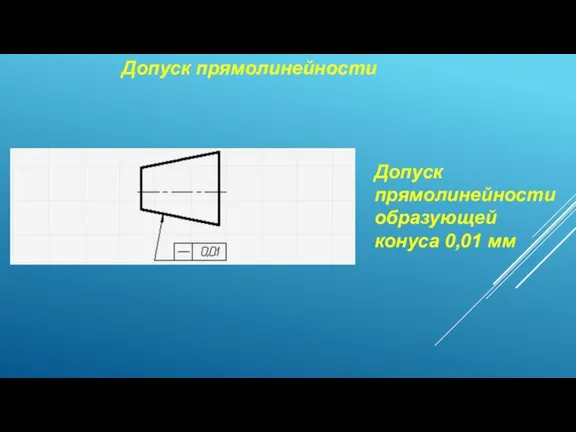 Допуск прямолинейности
Допуск прямолинейности Природа России в цифрах и загадках
Природа России в цифрах и загадках Нахождение произведения по предыдущему результату. Замена умножения сложением
Нахождение произведения по предыдущему результату. Замена умножения сложением Все действия с дробями
Все действия с дробями Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций