Содержание
- 2. Для раскрытия такого вида неопределенности необходимо: разделить все слагаемые числителя и знаменателя на переменную х в
- 3. На основании теоремы о пределе частного, суммы (разности) рассмотрим предел каждого слагаемого
- 4. б). Степень многочлена числителя больше степени многочлена знаменателя
- 5. в). степень многочлена числителя меньше степени многочлена знаменателя
- 6. Предел отношения двух многочленов при равен 1. если степень многочлена числителя меньше степени многочлена знаменателя, по
- 7. 2. Неопределенность вида . Метод раскрытия неопределенности такого вида зависит от выражения стоящего под знаком предела,
- 8. Разложим числитель и знаменатель на множители: Если числитель и знаменатель дробно-рациональной функции являются многочленами второй степени,
- 9. Для решения задачи необходимо Определить корни числителя и знаменателя Разложить многочлен на множители
- 10. Рассмотрим пример: Вычислим корни многочлена числителя и знаменателя, разложим числитель и знаменатель на множители:
- 11. б). выражение стоящее под знаком предела, содержит дробно-иррациональную функцию В этом случае для раскрытия неопределенности умножают
- 13. Рассмотрим пример, когда числитель дроби является иррациональным выражением Пример:
- 14. В этом случае и числитель и знаменатель содержат иррациональные выражения.
- 15. Первый замечательный предел Если выражение, стоящее под знаком предела содержит тригонометрические функции, то для раскрытия неопределенности
- 16. Рассмотрим пример
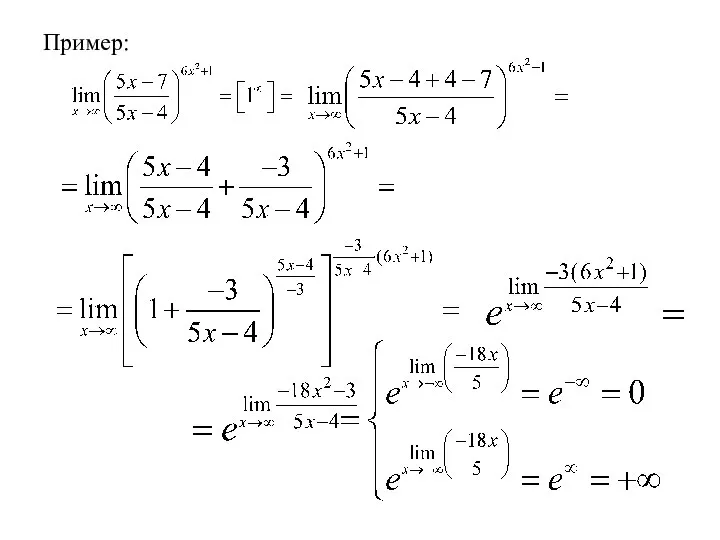
- 19. 3. Неопределенность вида Для раскрытия неопределенностей такого вида применяется второй замечательный предел: Рассмотрим пример:
- 20. Пример:
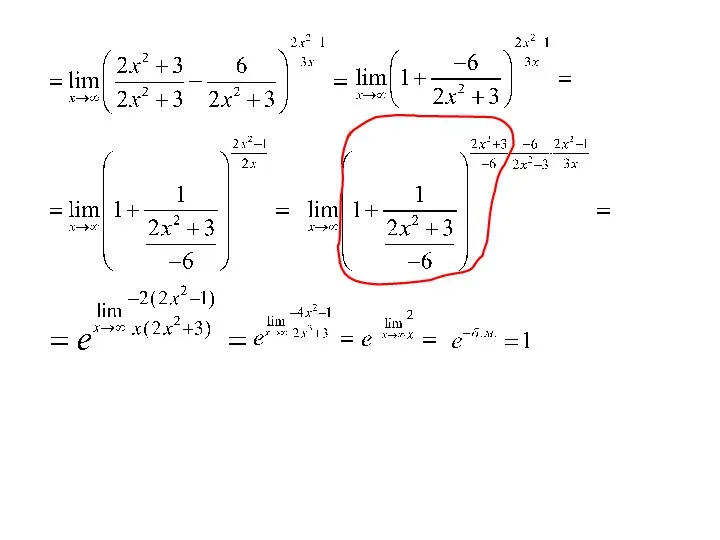
- 21. Пример:
- 23. Пример
- 24. Пример:
- 25. Пример: Пример:
- 27. Пример: Для решения задач данного типа, необходимо преобразовать выражение стоящее под знаком предела, используя свойства логарифмической
- 29. 4. Неопределенность вида Замечание: данный вид неопределенности возможен только при Выражение, стоящее под знаком предела представляет
- 30. Решение.
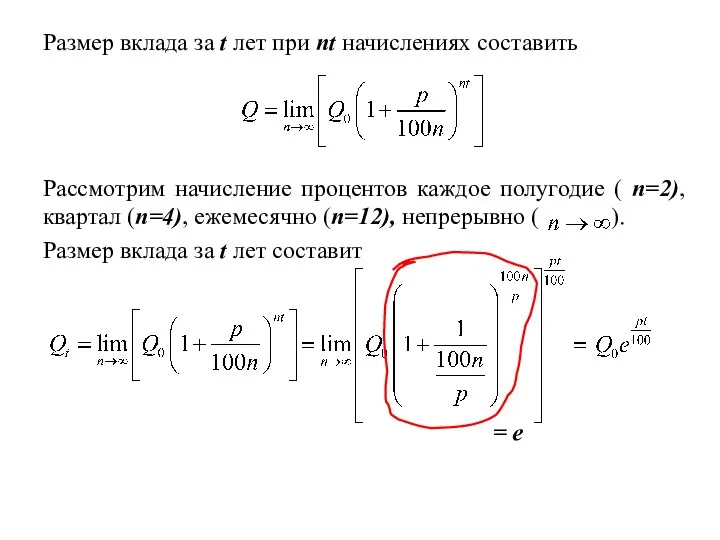
- 31. Задача о непрерывном начислении процентов Первоначальный вклад в банк составил Q0 денежных единиц. Банк выплачивает ежегодно
- 32. 2. Сложные проценты – размер вклада ежегодно увеличивается в одно и то же число раз равное
- 33. Размер вклада за t лет при nt начислениях составить Рассмотрим начисление процентов каждое полугодие ( n=2),
- 35. Скачать презентацию










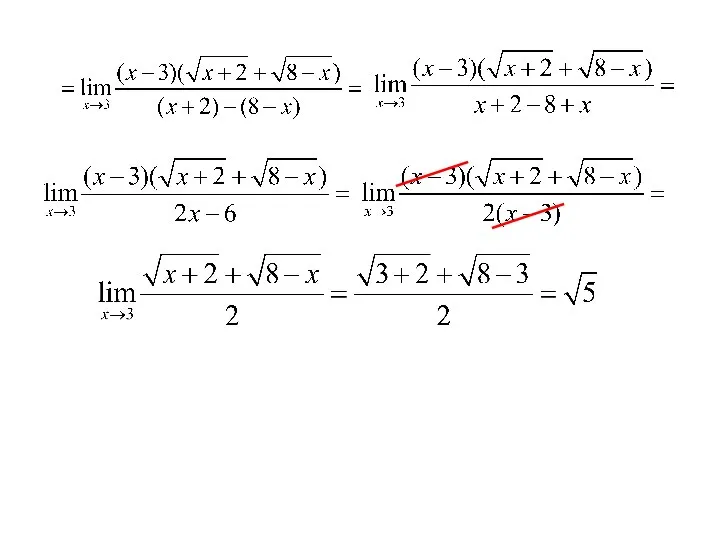




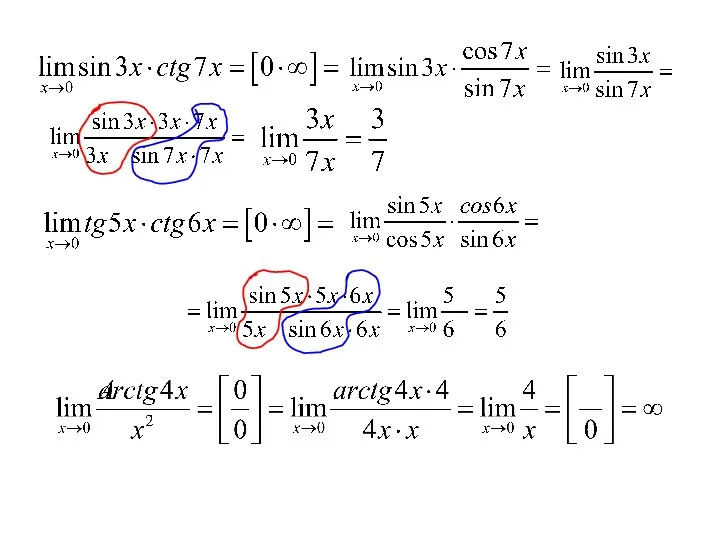


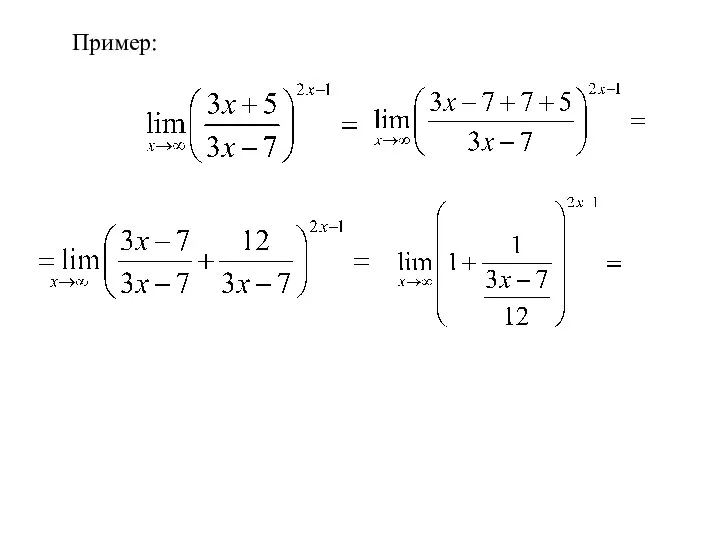


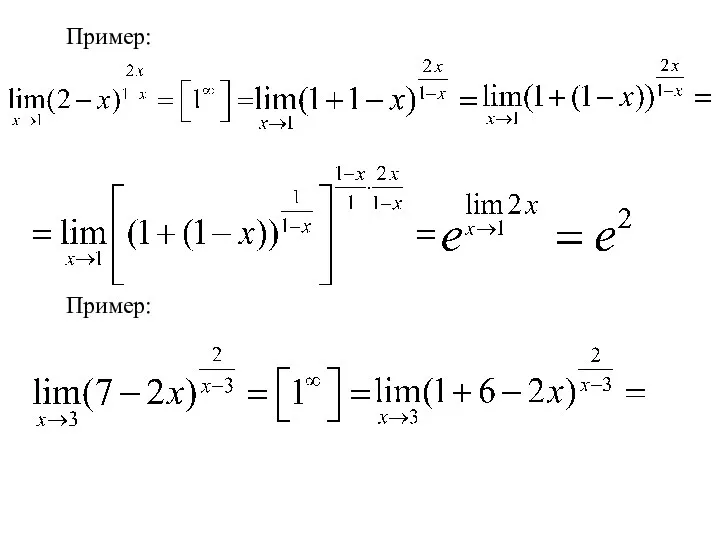
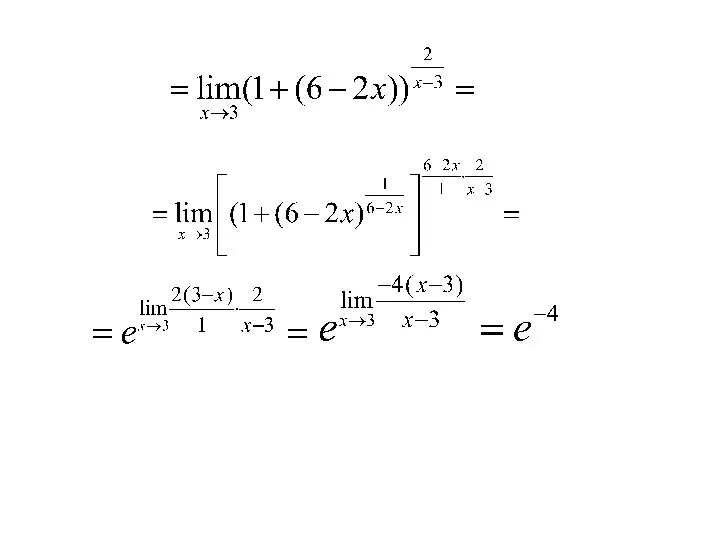

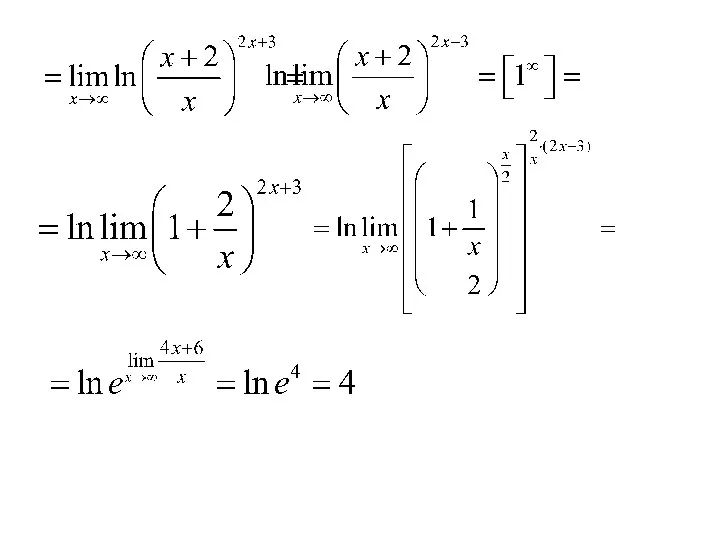




 Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях
Про Федота стрельца, аглицкого посла и геометрию! Сказка в 4-х действиях Методы и приемы решения дробно-рациональных уравнений, содержащих параметр
Методы и приемы решения дробно-рациональных уравнений, содержащих параметр Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Цифровая азбука
Цифровая азбука Теоремы синусов и косинусов
Теоремы синусов и косинусов Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Закон Ома. Решение задач
Закон Ома. Решение задач Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел
Сообщение по истории математики «Из истории позиционных систем счисления» Выполнила ученица 6 «А класса» Дивии Идегел Площадь полной поверхности призмы
Площадь полной поверхности призмы Комбинаторные задачи
Комбинаторные задачи Радианная мера угла
Радианная мера угла Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Vorlesung. Blatt 2
Vorlesung. Blatt 2 Соста числа 11
Соста числа 11 Тригонометрические уравнения
Тригонометрические уравнения Презентация на тему Стандартный вид числа 9 класс
Презентация на тему Стандартный вид числа 9 класс  Лекция 0
Лекция 0 Элементы математической статистики, комбинаторики и теории вероятностей
Элементы математической статистики, комбинаторики и теории вероятностей Презентация на тему Плоскость. Прямая. Луч
Презентация на тему Плоскость. Прямая. Луч  Симметрия. 9 класс
Симметрия. 9 класс Алгоритм Евклида
Алгоритм Евклида Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Призмы. Виды призм
Призмы. Виды призм Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Периметр и площадь
Периметр и площадь Матрицы и определители
Матрицы и определители