Содержание
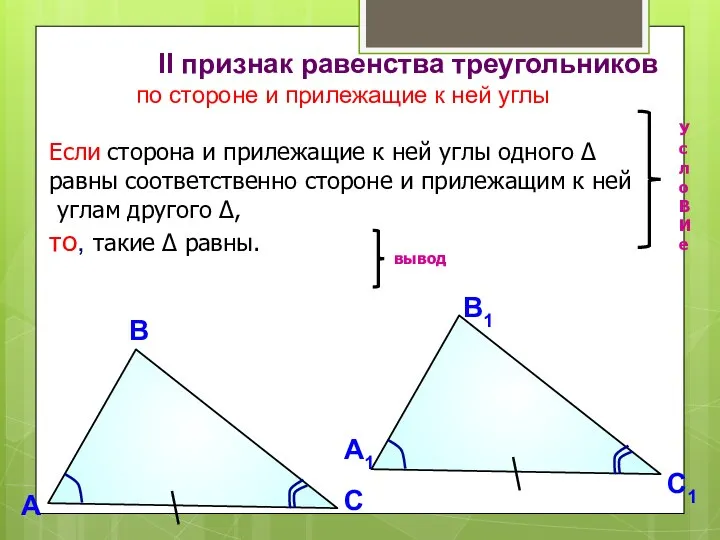
- 2. II признак равенства треугольников по стороне и прилежащие к ней углы Если сторона и прилежащие к
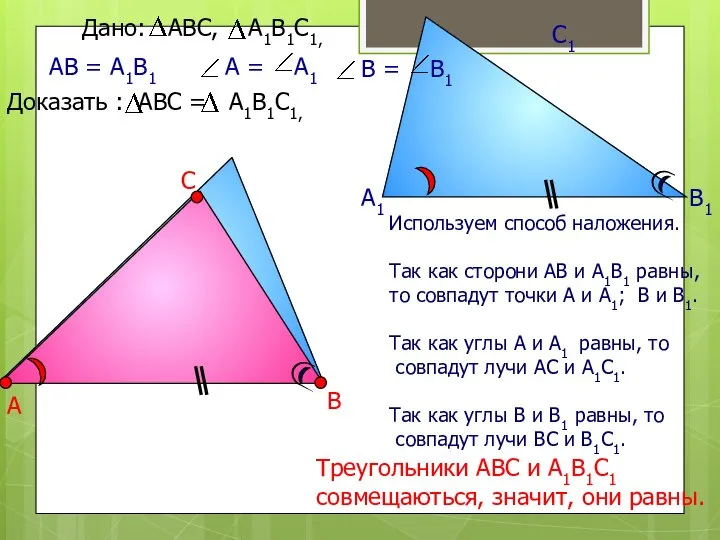
- 3. А В С А1 В1 С1 АВ = А1В1 Треугольники АВС и А1В1С1 совмещаються, значит, они
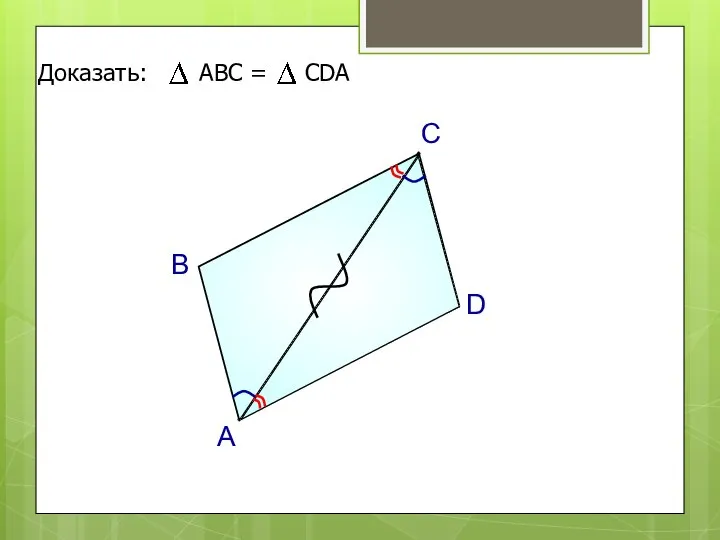
- 4. А В С D
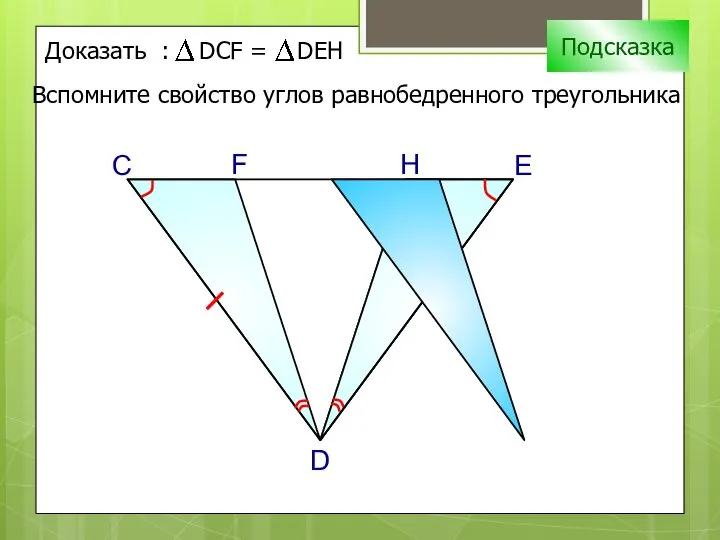
- 5. С H D F E Подсказка Вспомните свойство углов равнобедренного треугольника
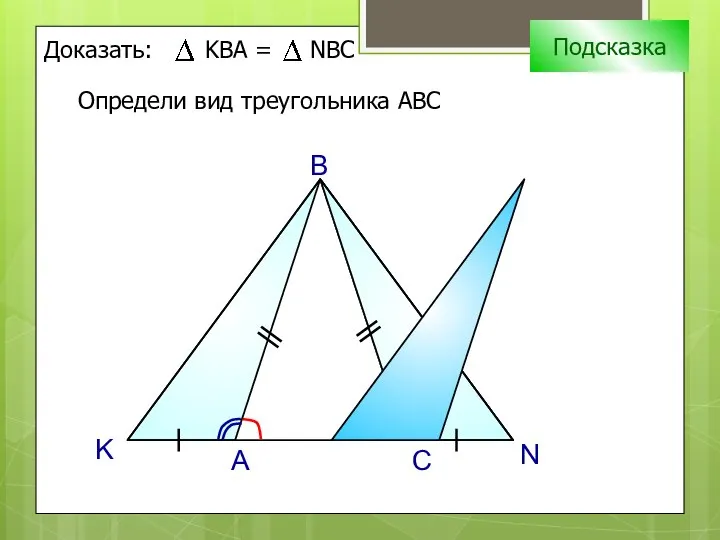
- 6. K N A B Подсказка Определи вид треугольника АВС C
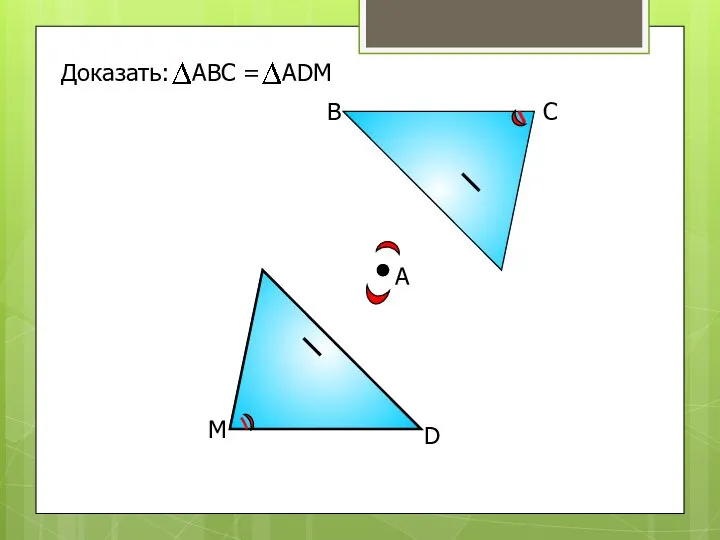
- 7. D М А В С
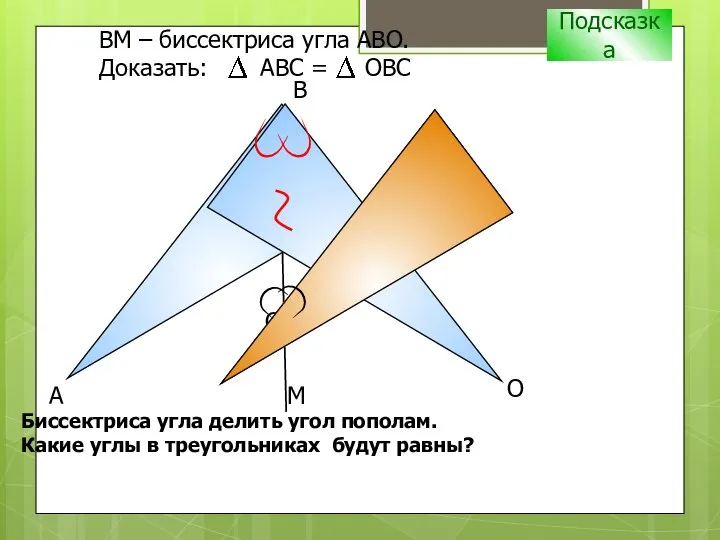
- 8. С B А ВM – биссектриса угла АВО. Доказать: АВС = ОВС Подсказка Биссектриса угла делить
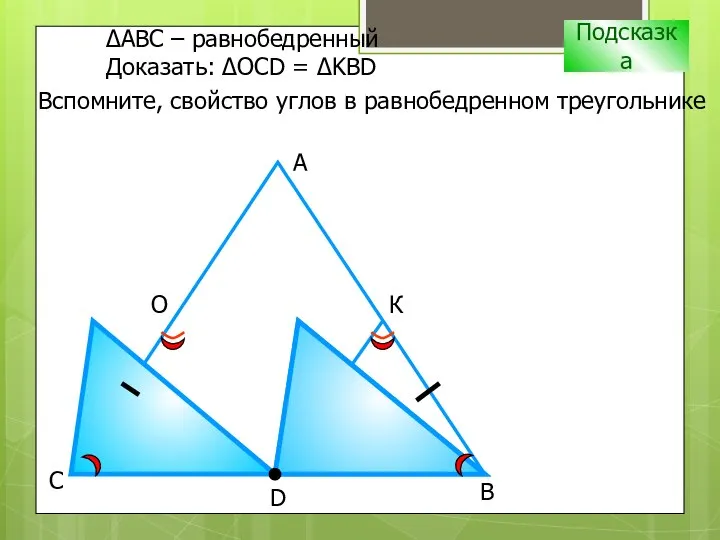
- 9. D В С А О К Подсказка Вспомните, свойство углов в равнобедренном треугольнике ∆АВС – равнобедренный
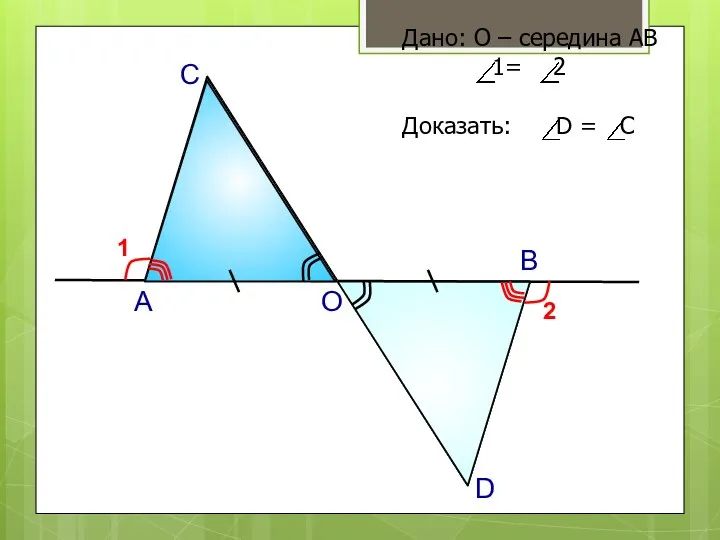
- 10. А О В С D 1 2
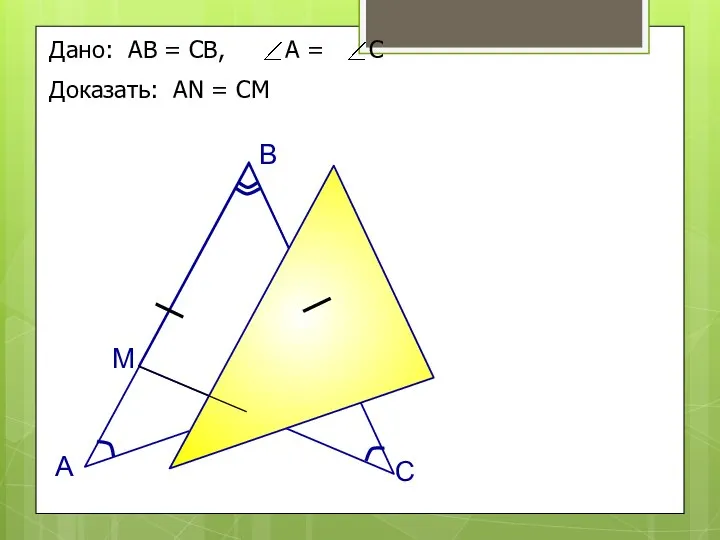
- 11. Дано: АВ = СВ, А = С Доказать: АN = СM А B C M N
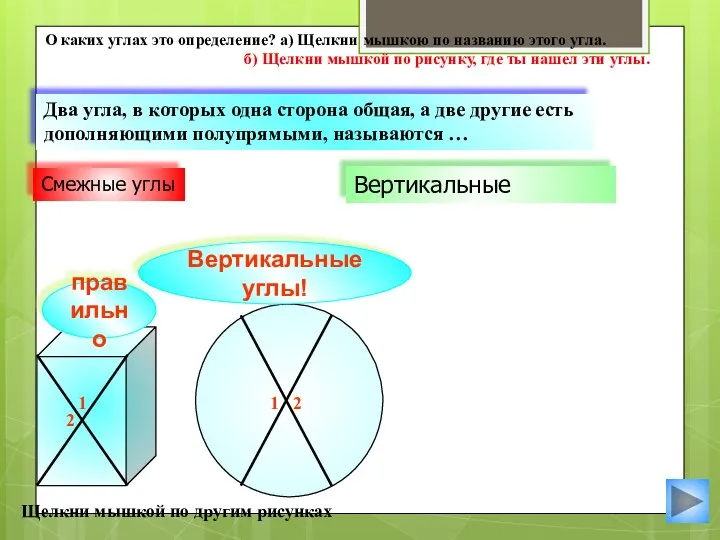
- 12. Вертикальные углы! Вертикальные Два угла, в которых одна сторона общая, а две другие есть дополняющими полупрямыми,
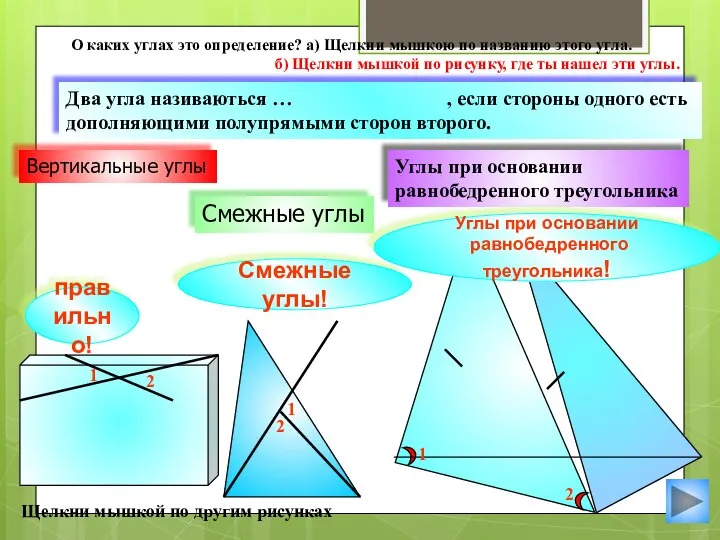
- 13. Смежные углы Углы при основании равнобедренного треугольника Два угла називаються … , если стороны одного есть
- 14. Каменный треугольник. Невозможные фигуры вдохновляют художников и даже скульпторов. Экскурс «Замечательные треугольники» «По страницам всемирной сети
- 15. Треугольник Пенроуза или трибар. Из коллекции невозможных объектов. Кажется, что мы видим три бруска квадратного сечения
- 16. Треугольник из кубов Геометрические фигуры – лучший источник вдохновения для изобретения невозможных объектов. Например, возьмем простой
- 17. Тройное домино Из коллекции невозможных объектов.
- 18. На примере первого трибара можно было увидеть лишь одно невозможное соединение, а в этой фигуре –
- 20. Скачать презентацию





 Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Графы
Графы Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Векторная алгебра
Векторная алгебра Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Логарифм
Логарифм Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Головоломки и занимательные задачи
Головоломки и занимательные задачи 1_1_matritsy (1)
1_1_matritsy (1) Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Кратные интегралы
Кратные интегралы Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа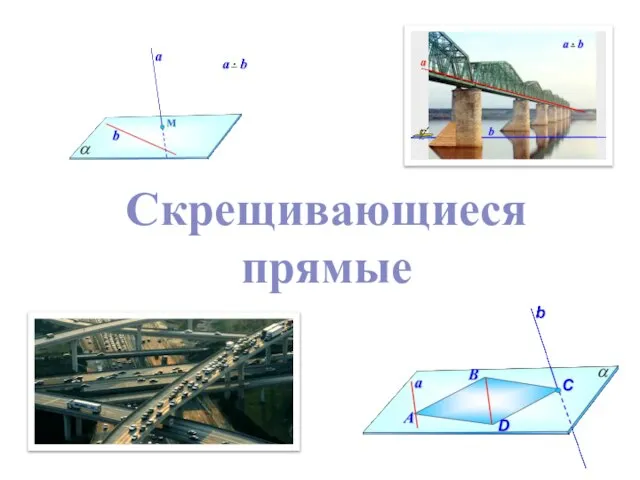 Скрещивающиеся прямые
Скрещивающиеся прямые Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Упрощение логических операций
Упрощение логических операций Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Проценты
Презентация на тему Проценты  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Математический анализ. Лекция 1
Математический анализ. Лекция 1 Движение. Поворот
Движение. Поворот Случаи вычитания 11-
Случаи вычитания 11- Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Блез Паскаль
Блез Паскаль Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Выполни вычисления
Выполни вычисления Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15