- Главная
- Математика
- Введение в анализ. Предел функции

Содержание
- 2. § 1. Предел функции
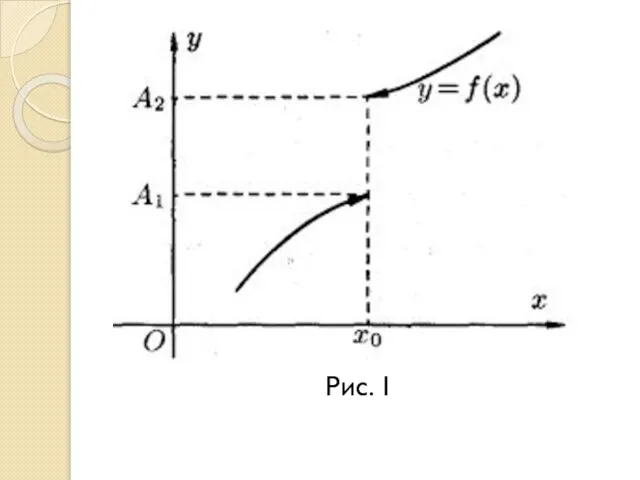
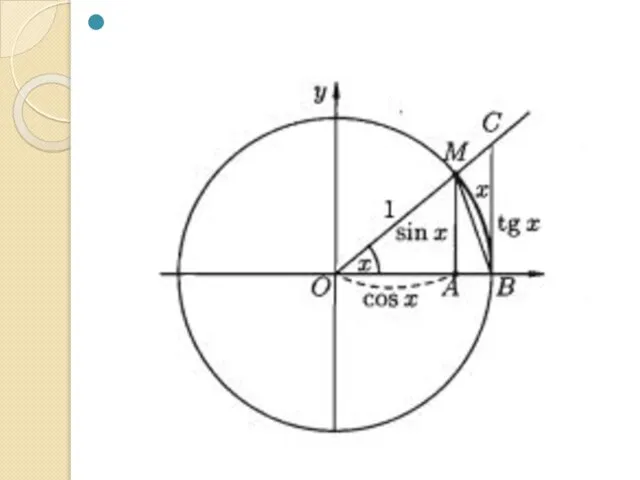
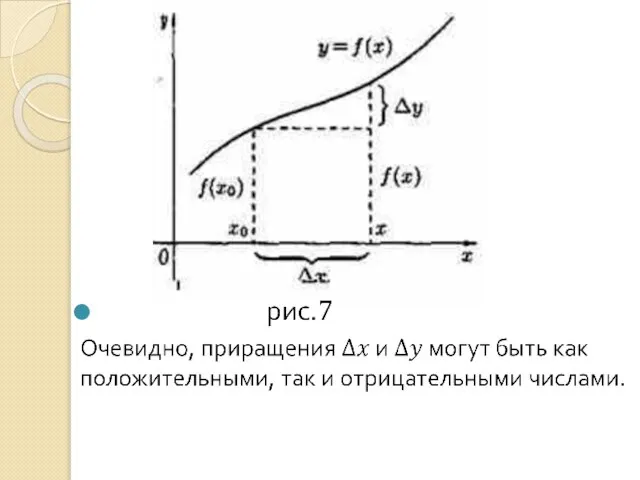
- 7. Рис. 1
- 70. Ниже приведены важнейшие эквивалентности, которые используются при вычислении пределов:
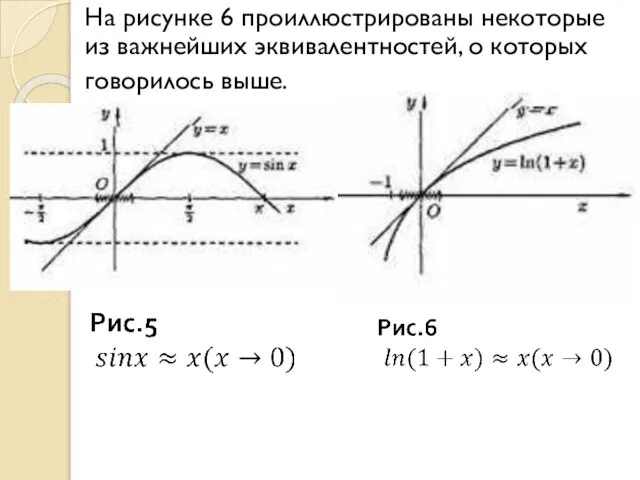
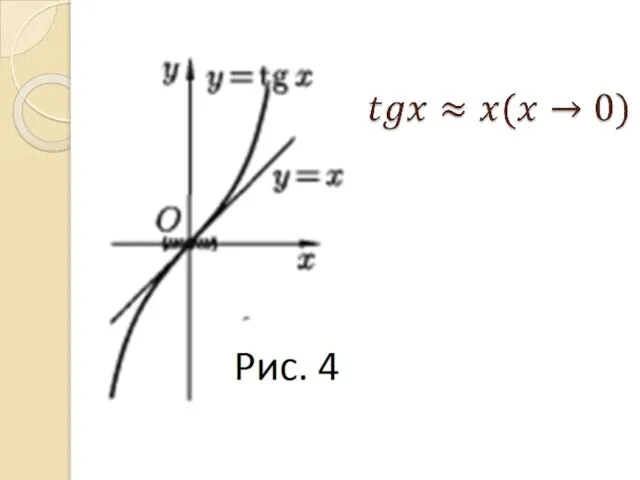
- 76. На рисунке 6 проиллюстрированы некоторые из важнейших эквивалентностей, о которых говорилось выше.
- 111. Из приведенных выше теорем следует: всякая элементарная функция непрерывна в каждой точке, в которой она определена.
- 122. Скачать презентацию
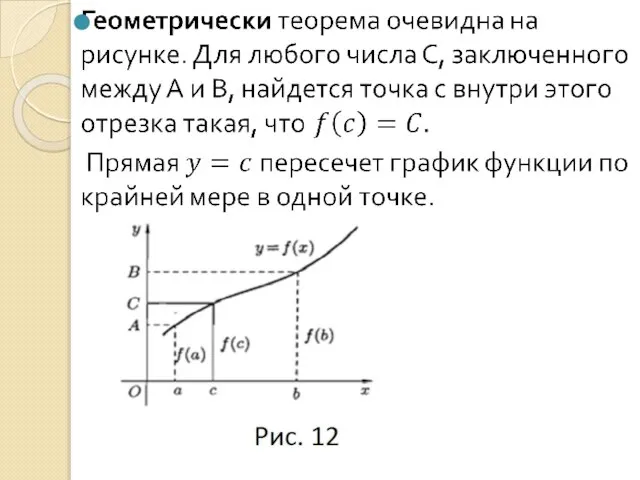
Слайд 7Рис. 1
Рис. 1
Слайд 70Ниже приведены важнейшие эквивалентности, которые используются при вычислении пределов:
Ниже приведены важнейшие эквивалентности, которые используются при вычислении пределов:

Слайд 76На рисунке 6 проиллюстрированы некоторые из важнейших эквивалентностей, о которых
говорилось выше.
На рисунке 6 проиллюстрированы некоторые из важнейших эквивалентностей, о которых
говорилось выше.
Слайд 111Из приведенных выше теорем следует:
всякая элементарная функция непрерывна в каждой точке,
Из приведенных выше теорем следует: всякая элементарная функция непрерывна в каждой точке,

в которой она определена.
Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.
Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.























































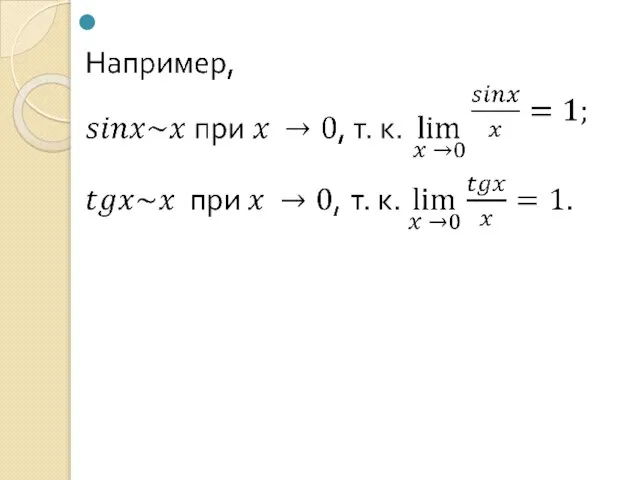

















































 Шар. Сфера
Шар. Сфера Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Реши примеры
Реши примеры Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Решение задач по теме Площади фигур
Решение задач по теме Площади фигур Порядковый счёт в пределах 10
Порядковый счёт в пределах 10 Делители и кратные. 8.09.12 Классная работа.
Делители и кратные. 8.09.12 Классная работа. Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц
Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц Планиметрия и стериометрия
Планиметрия и стериометрия Основы тригонометрии
Основы тригонометрии Сечение многогранника плоскостью
Сечение многогранника плоскостью Предел функции в точке
Предел функции в точке Функции и их графики
Функции и их графики Действия с десятичными дробями. Магницкий Леонтий Филиппович
Действия с десятичными дробями. Магницкий Леонтий Филиппович Определенный интеграл
Определенный интеграл Решаем задачи
Решаем задачи Разложение разности квадратов на множители
Разложение разности квадратов на множители Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Конкурсы. Разминка
Конкурсы. Разминка Числовые последовательности
Числовые последовательности Измеряй и сравнивай
Измеряй и сравнивай Единицы измерения времени
Единицы измерения времени Статистический анализ зависимостей между гидрологическими переменными (лекция 11)
Статистический анализ зависимостей между гидрологическими переменными (лекция 11) Решение задачи дуффинга регуляризованными методами неполного прогноза
Решение задачи дуффинга регуляризованными методами неполного прогноза Область определения функции
Область определения функции Аксиомы стереометрии
Аксиомы стереометрии Дидактический материал. Проверочные работы. Начальные понятия геометрии
Дидактический материал. Проверочные работы. Начальные понятия геометрии Решение задач на разностное сравнение 2 класс - Презентация
Решение задач на разностное сравнение 2 класс - Презентация