Занимательная математика .Окружность

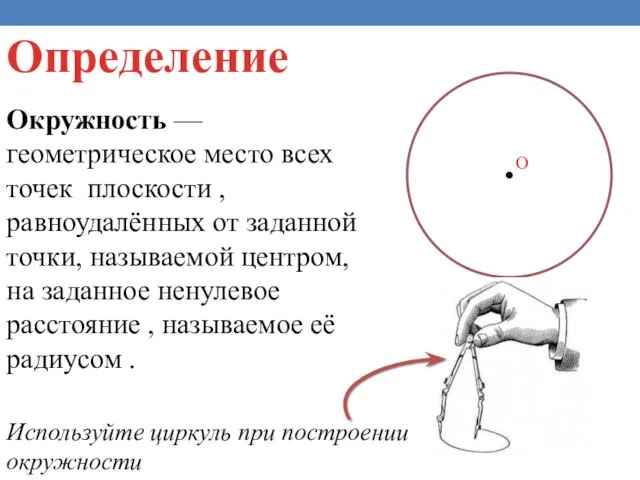
Окружность — геометрическое место всех точек плоскости , равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние , называемое её радиусом .
О
Определение
Используйте циркуль при построении окружности

О
A
B
Центр окружности -точка, от которой равноудалены на заданное расстояние все точки окружности. О -центр окружности
Отрезок, соединяющий любую точку окружности с ее центром, а также его длина, называется радиусом окружности.
ОA- радиус окружности
Диаметром окружности называется хорда данной окружности, проходящая через ее центр.
Отрезок, соединяющий две точки окружности, называется хордой окружности, а также хордой ограниченного ей круга.
AB- хорда, проходящая через ее центр О
ВСПОМНИ!!!

Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.
Свойства окружности

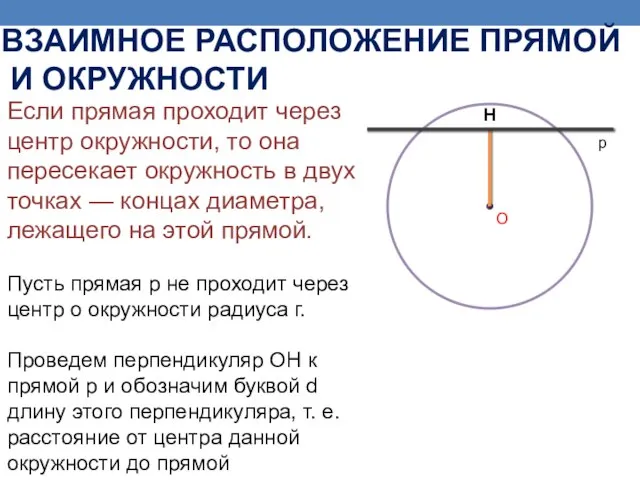
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, лежащего на этой прямой.
Пусть прямая р не проходит через центр о окружности радиуса г.
Проведем перпендикуляр ОН к прямой р и обозначим буквой d длину этого перпендикуляра, т. е. расстояние от центра данной окружности до прямой
О
H
p
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ
И ОКРУЖНОСТИ

d < г
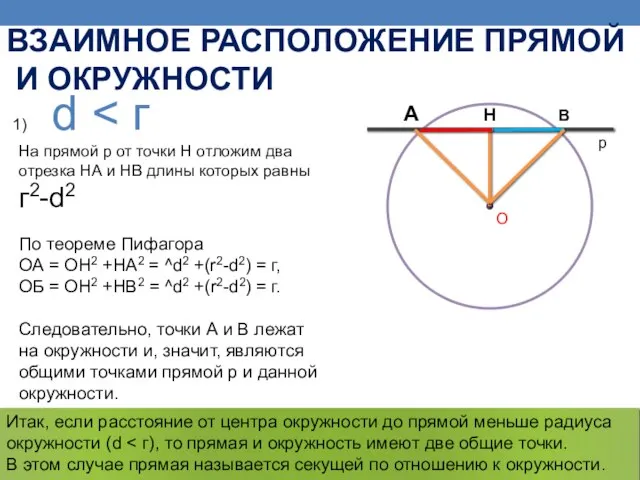
На прямой р от точки Н отложим два отрезка НА и НВ длины которых равны г2-d2
По теореме Пифагора
ОА = ОН2 +НА2 = ^d2 +(r2-d2) = г,
ОБ = OH2 +НВ2 = ^d2 +(r2-d2) = г.
Следовательно, точки А и В лежат на окружности и, значит, являются общими точками прямой р и данной окружности.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ
И ОКРУЖНОСТИ
О
А
B
H
p
Итак, если расстояние от центра окружности до прямой меньше радиуса окружности (d < г), то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.

2) d = г
В этом случае ОН= г, т. е. точка Н лежит на окружности и, значит, является общей точкой прямой и окружности
Прямая р и окружность не имеют других общих точек, так как для любой точки М прямой р, отличной от точки Н, ОМ > ОН = г (наклонная ОМ больше перпендикуляра ОН), и, следовательно, точка М не лежит на окружности.
О
M
H
p
Итак, если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ
И ОКРУЖНОСТИ

d > г
В этом случае ОН > г, поэтому для любой точки М прямой р ОМ > ОН > г
Следовательно, точка М не лежит на окружности.
О
M
H
p
r
Итак, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ
И ОКРУЖНОСТИ

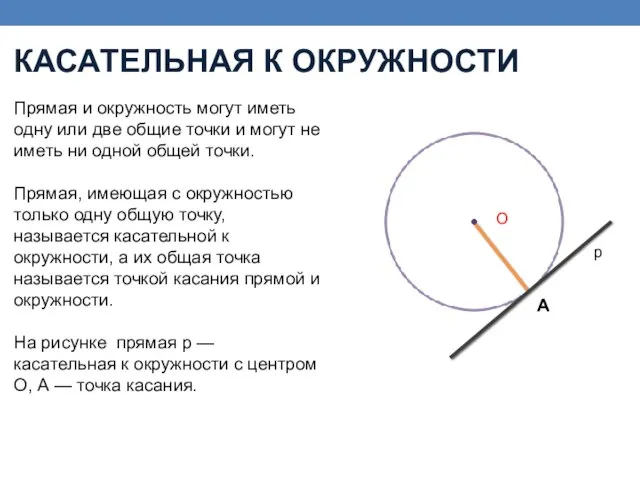
Прямая и окружность могут иметь одну или две общие точки и могут не иметь ни одной общей точки.
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
На рисунке прямая р — касательная к окружности с центром О, А — точка касания.
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
О
A
p

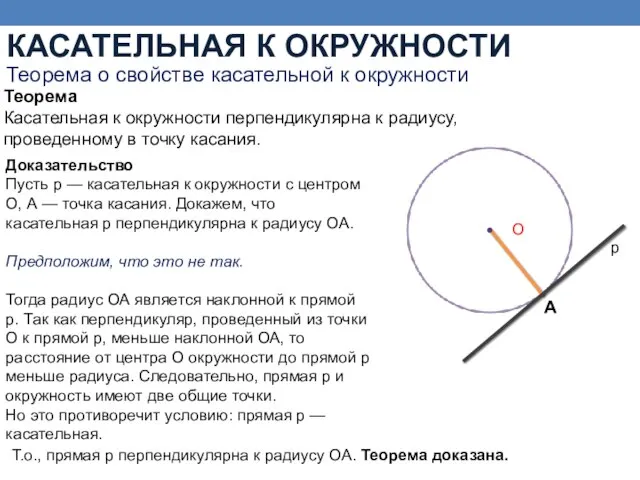
Доказательство
Пусть р — касательная к окружности с центром О, А — точка касания. Докажем, что касательная р перпендикулярна к радиусу ОА.
Предположим, что это не так.
Тогда радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведенный из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки.
Но это противоречит условию: прямая р — касательная.
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
О
A
p
Теоремa о свойстве касательной к окружности
Теорема
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Т.o., прямая р перпендикулярна к радиусу ОА. Теорема доказана.

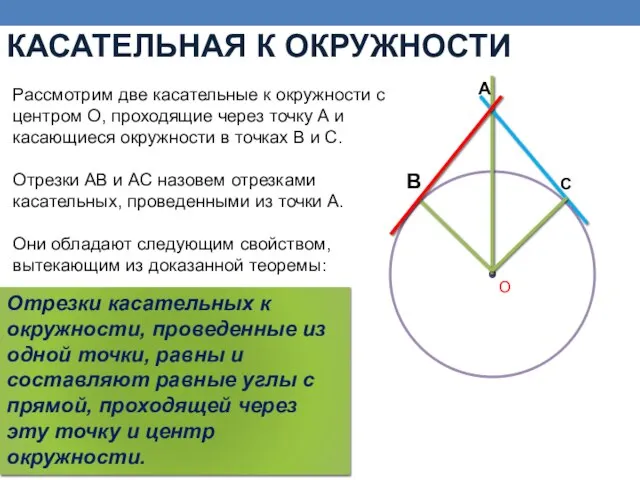
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Рассмотрим две касательные к окружности с центром О, проходящие через точку А и касающиеся окружности в точках В и С.
Отрезки АВ и АС назовем отрезками касательных, проведенными из точки А.
Они обладают следующим свойством, вытекающим из доказанной теоремы:
О
B
C
A
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

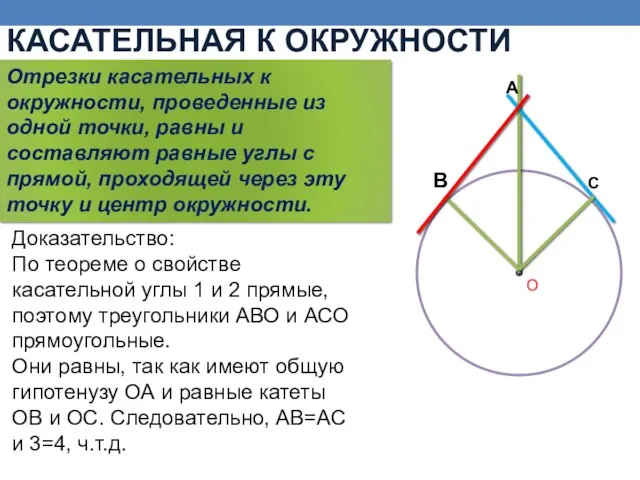
Доказательство:
По теореме о свойстве касательной углы 1 и 2 прямые, поэтому треугольники АВО и АСО прямоугольные.
Они равны, так как имеют общую гипотенузу ОА и равные катеты ОВ и ОС. Следовательно, АВ=АС и 3=4, ч.т.д.
О
B
C
A
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ

Доказательство
Из условия теоремы следует, что данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой. Поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку. Но это и означает, что данная прямая является касательной к окружности. Теорема доказана.
Теорема, обратная теореме о свойстве касательной (признак касательной)
Теорема
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

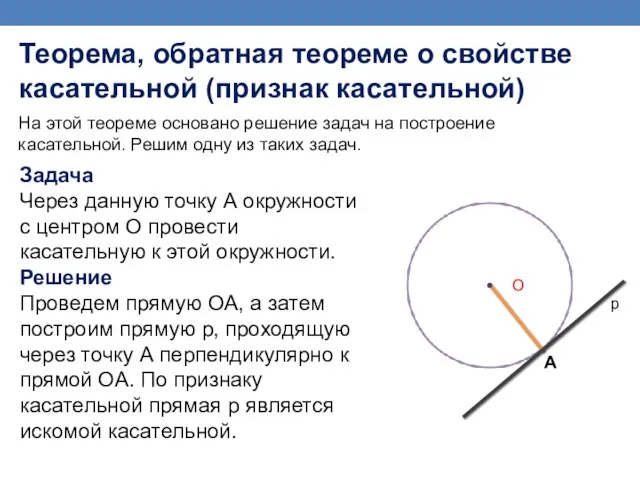
На этой теореме основано решение задач на построение касательной. Решим одну из таких задач.
Теорема, обратная теореме о свойстве касательной (признак касательной)
Задача
Через данную точку А окружности с центром О провести касательную к этой окружности.
Решение
Проведем прямую ОА, а затем построим прямую р, проходящую через точку А перпендикулярно к прямой ОА. По признаку касательной прямая р является искомой касательной.
О
A
p

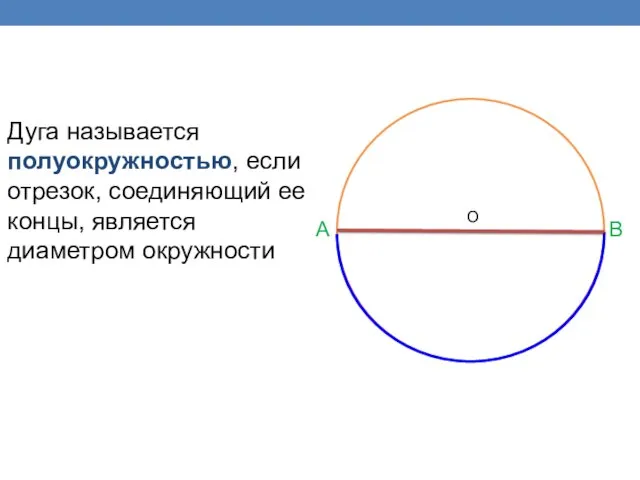
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности
A
B
O

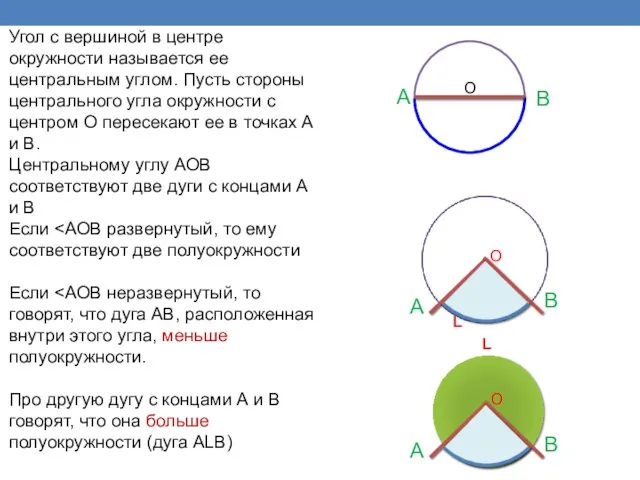
Угол с вершиной в центре окружности называется ее центральным углом. Пусть стороны центрального угла окружности с центром О пересекают ее в точках А и В.
Центральному углу АОВ соответствуют две дуги с концами А и В
Если <АОВ развернутый, то ему соответствуют две полуокружности
Если <АОВ неразвернутый, то говорят, что дуга АВ, расположенная внутри этого угла, меньше полуокружности.
Про другую дугу с концами А и В говорят, что она больше полуокружности (дуга ALB)
A
B
O
О
A
B
О
A
B
L
L

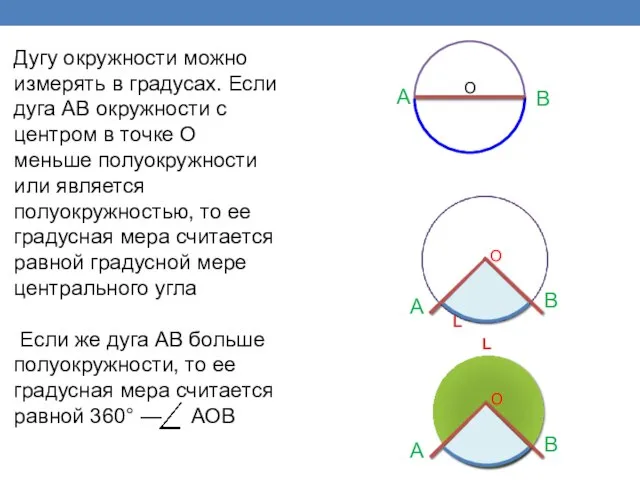
A
B
O
О
A
B
О
A
B
L
L
Дугу окружности можно измерять в градусах. Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла
Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360° — АОВ

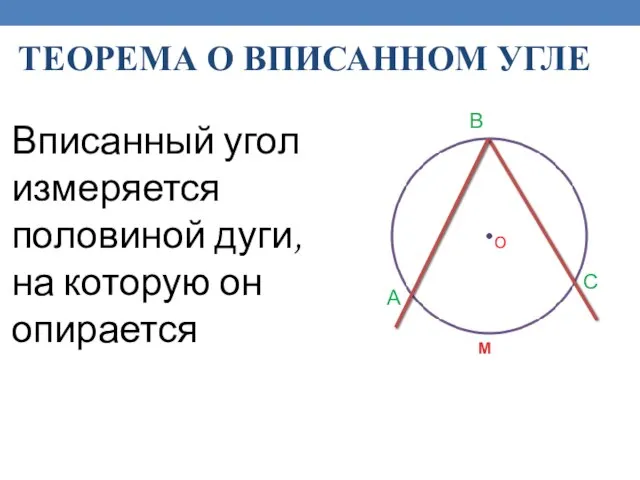
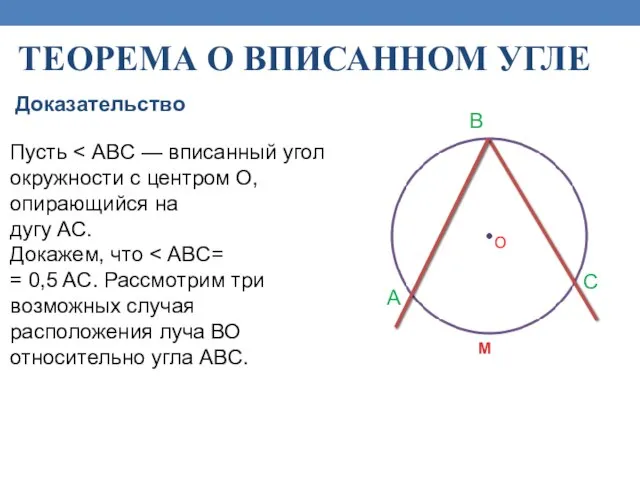
ТЕОРЕМА О ВПИСАННОМ УГЛЕ
Вписанный угол измеряется половиной дуги, на которую он опирается
О
A
B
M
C

ТЕОРЕМА О ВПИСАННОМ УГЛЕ
Пусть < ABC — вписанный угол окружности с центром О, опирающийся на
дугу АС.
Докажем, что < ABC=
= 0,5 AC. Рассмотрим три возможных случая расположения луча ВО относительно угла ABC.
О
A
B
M
C
Доказательство

Три возможных случая расположения луча ВО относительно угла АВС
Луч ВО совпадает с одной из сторон угла АВС (Рис.a)
Луч ВО делит угол АВС на два угла (Рис. б)
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла (Рис. в)

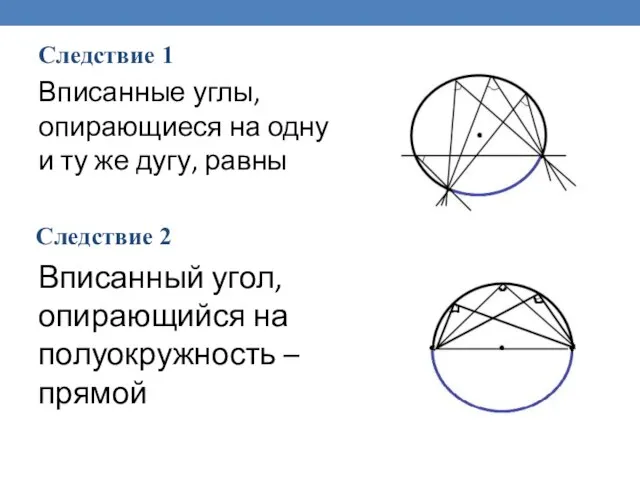
Следствие 1
Следствие 2
Вписанные углы, опирающиеся на одну и ту же дугу, равны
Вписанный угол, опирающийся на полуокружность – прямой

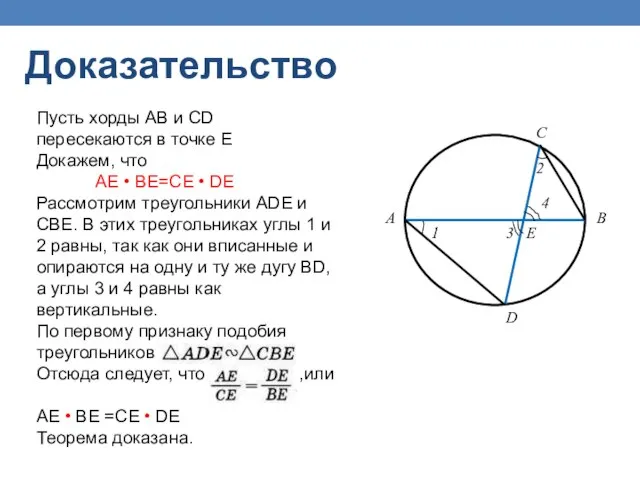
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды
B
А
С
D
E
1
2
3
4
Теорема

Пусть хорды АВ и CD пересекаются в точке Е
Докажем, что
АЕ • ВЕ=СЕ • DE
Рассмотрим треугольники ADE и
СBE. В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 3 и 4 равны как вертикальные.
По первому признаку подобия треугольников
Отсюда следует, что ,или
АЕ • ВЕ =СЕ • DE
Теорема доказана.
B
А
С
D
E
1
2
3
4
Доказательство