Содержание
- 2. Цілі та задачі Мета роботи: вивчення застосування полярної, циліндричної, сферичної систем координат до розв’язування задач. Об’єкт
- 3. Вивчити особливості введення полярної, циліндричної, сферичної систем координат та їх зв'язок з декартовою системою. З’ясувати деякі
- 4. Структура роботи Робота складається з трьох розділів – теоретичної частини та практичної. В першому розділі розглянуто
- 5. Системи координат та координатний метод Декартова система координат Три взаємно перпендикулярні осі Ох, Оу, Оz, які
- 6. Полярні координати Зв’язок між полярними і декартовими координатами: Відстань між точками у поярній системі координат: (1.1)
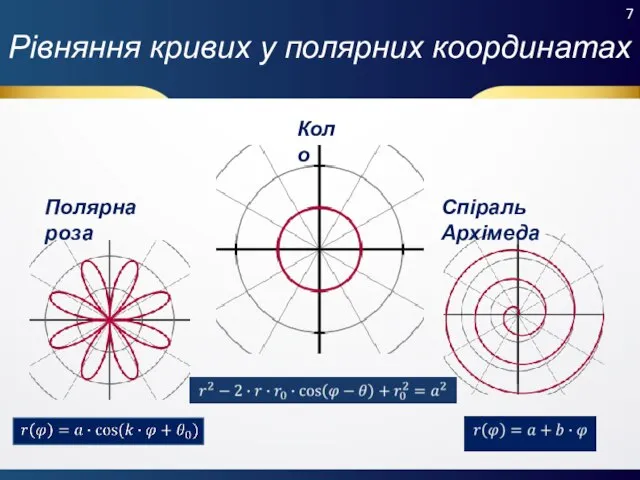
- 7. Рівняння кривих у полярних координатах Коло Полярна роза Спіраль Архімеда 7
- 8. Застосування полярної системи координат для розв’язання геометричних задач Приклад (власний) Кола радіусом R та 2R ззовні
- 9. Теорема косинусів Доведення теореми косинусів у шкільному підручнику:
- 10. Теорема косинусів Доведення у полярній системі координат: Теорему доведено.
- 11. Сферичні координати Зв’язок між сферичними і декартовими координатами: O
- 12. Застосування криволінійних координат для розв’язання задач Розв’язати систему: Задача(авторська)
- 13. _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
- 14. Циліндричні координати Зв’язок між циліндричними і декартовими координатами: C 14
- 15. Застосуємо перехід до узагальненої циліндричної системи координат: Застосування циліндричних координат 1 2
- 16. Висновки З’ясовано основні області застосування криволінійних систем координат та їх зв'язок з декартовою системою; Запропоновано метод
- 18. Скачать презентацию














 Презентация по математике "Ломаные числа" -
Презентация по математике "Ломаные числа" -  Умножение числа 0 и на число 0 Умножение числа 1 и на число 1
Умножение числа 0 и на число 0 Умножение числа 1 и на число 1 Методы корреляционно-регрессионного анализа фондового рынка
Методы корреляционно-регрессионного анализа фондового рынка Статистическая проверка статистических гипотез
Статистическая проверка статистических гипотез Математика и техника. Их связь и значение
Математика и техника. Их связь и значение Групповое задание
Групповое задание Коррекция нелинейных систем
Коррекция нелинейных систем Перемещение тела на плоскости (задача)
Перемещение тела на плоскости (задача) Теорема Пифагора
Теорема Пифагора Таблица умножения на 2
Таблица умножения на 2 Повторение и закрепление. Итоговое повторение за год. 4 класс
Повторение и закрепление. Итоговое повторение за год. 4 класс Прямоугольник. Ромб. Квадрат
Прямоугольник. Ромб. Квадрат Что такое разложение на множители и зачем оно нужно
Что такое разложение на множители и зачем оно нужно Гомотетия. Подобие фигур
Гомотетия. Подобие фигур Элементы математической логики
Элементы математической логики История возникновения науки геометрии
История возникновения науки геометрии Презентация на тему Окружность ее центр и радиус
Презентация на тему Окружность ее центр и радиус 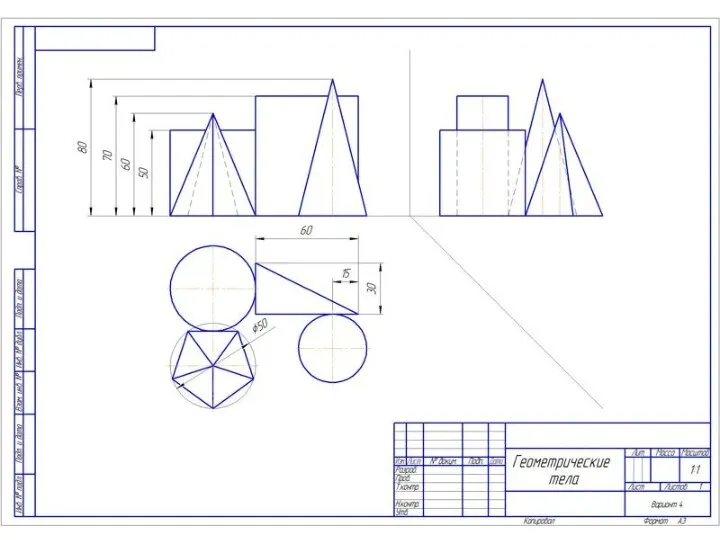 Геометрические тела. 9 класс
Геометрические тела. 9 класс Формирование регулятивных УУД у младших школьников при изучении геометрического материала
Формирование регулятивных УУД у младших школьников при изучении геометрического материала Стандартизация в различных сферах. Сущность стандартизации
Стандартизация в различных сферах. Сущность стандартизации Без знаний дробей никто не может признаваться знающим арифметику
Без знаний дробей никто не может признаваться знающим арифметику Признак перпендикулярности плоскостей
Признак перпендикулярности плоскостей Kоординатная плоскость
Kоординатная плоскость Средние величины
Средние величины Математика. Роль математики в жизни людей и общества
Математика. Роль математики в жизни людей и общества Действия с натуральными числами. Сложение и вычитание
Действия с натуральными числами. Сложение и вычитание Решение уравнений
Решение уравнений Презентация на тему Римские цифры (3 класс)
Презентация на тему Римские цифры (3 класс)