Элементы комбинаторики

"Три пути ведут к знанию. Путь размышлений - самый благородный, путь подражания - самый лёгкий, путь опыта - самый горький".
Конфуций
(551г. до н. э.)

Используйте действия сложения и вычитания
12
0
-4
100⅛
-3,04
Дополните до единицы:
+(-11) или -11
+1 или –(-1)
+5 или -(-5)
+(-99⅛) или -99⅛
+4,04 или –(-4,04)

Какую закономерность вы заметили?
Добавьте ещё два члена последовательности чисел:
-8; -6; -4; -2; …
-1; 1; -3; 3; …
1/2; -2/3; 3/4; -4/5;...
0; 2
-5; 5
5/6;-6/7

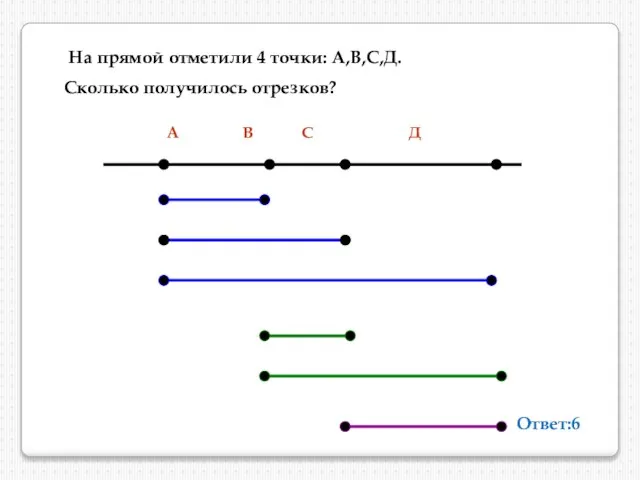
На прямой отметили 4 точки: А,В,С,Д.
Сколько получилось отрезков?
А В С Д
Ответ:6

Известно, что |а|=15;|в|=7.
1. Найдите числа а и в
2. Чему равны эти числа, если:
а+в=-8
-а+в=8
-а-в=-22
а×в=105
а×в=-105
а=-15; в=7
а=-15; в=-7
а=15; в=7
а=15; в=7 или ?
а=-15;в=7 или ?
а=15 или а=-15;
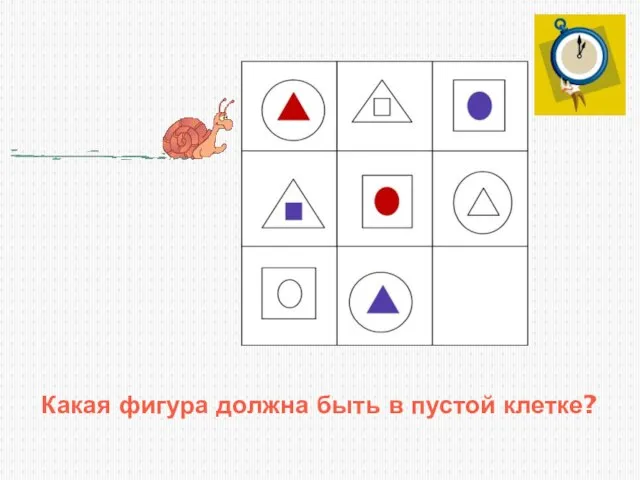
в=7 или в=-7

Какая фигура должна быть в пустой клетке?

Вопрос:
Что же такое КОМБИНАТОРИКА?

м
б
24.01.2012
о
и
н
а
т
о
р
и
к
а
Термин «комбинаторика» был введён в математический обиход немецким философом, математиком Лейбницем, который в 1666 году опубликовал труд «Рассуждения о комбинаторном искусстве».
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями.
к

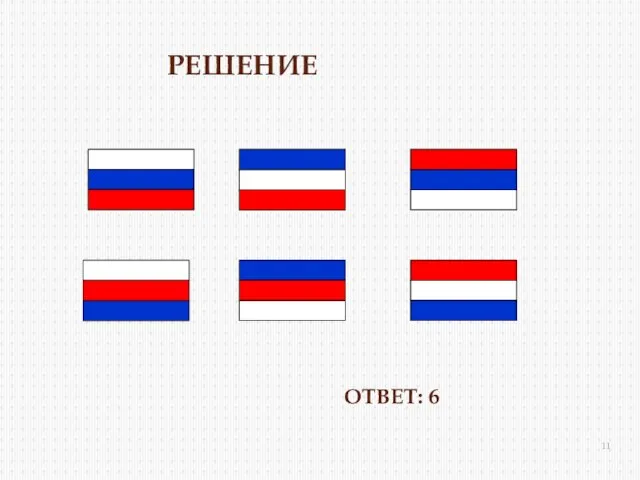
Задача 1
Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой?

ОТВЕТ: 6
РЕШЕНИЕ

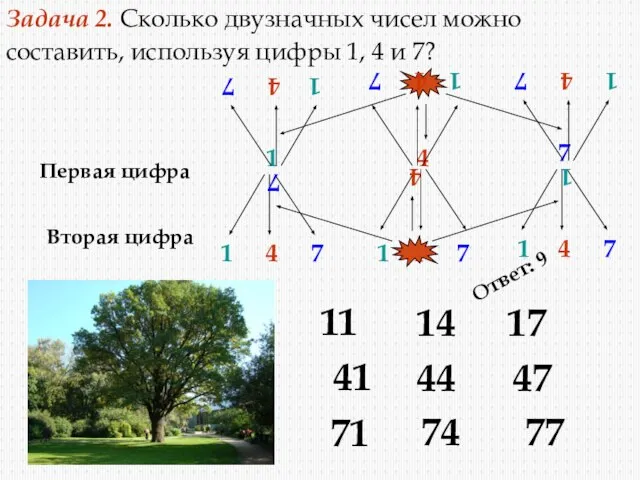
Задача 2. Сколько двузначных чисел можно составить, используя цифры
1, 4 и 7?
Первая цифра 1
Первая цифра 4
Первая цифра 7
14
17
41
44
47
71
74
77
11

Задача 2. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?
Первая цифра
Вторая цифра
1
4
7
1
4
7
1
4
7
1
4
7
11
14
17
41
44
47
71
74
77
Ответ: 9

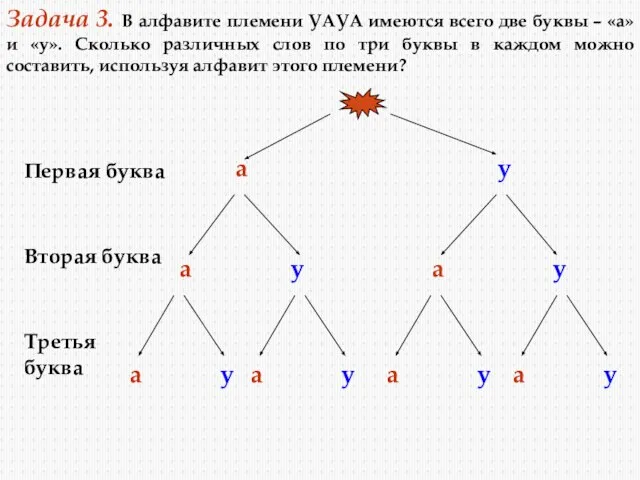
Задача 3. В алфавите племени УАУА имеются всего две буквы – «а» и «у». Сколько различных слов по три буквы в каждом можно составить, используя алфавит этого племени?
Первая буква
Вторая буква
а
у
а
у
а
у
Третья
буква
а
у
а
у
а
у
а
у

ааа
аау
ауа
ауу
уаа
уау
ууа
ууу
Ответ: 8

Правило умножения.
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А,В) в указанном порядке можно осуществить mn способами.
При этом число способов выбора второго элемента зависит от того, как именно выбран первый элемент.

Поэт-модернист написал стихотворение, в котором первая строчка – «Хочу пойти гулять куда-нибудь», а остальные строки все разные и получены из первой перестановкой слов. Какое наибольшее количество строк может быть в этом стихотворении?
ЗАДАЧА 4
Ответ: 24

Лёня 5 раз бросал монету и каждый раз записывал, что у него выпало- «орёл» или «решка». Получилась последовательность из пяти букв: ОРРОО.
А сколько всего существует вариантов таких последовательностей?
Задача 5
Ответ: 32

Задача 6
В розыгрыше чемпионата по футболу участвуют 12 команд. Сколькими способами могут быть распределены:
а)золотая медаль;
б) золотая и серебряная медали;
в)золотая, серебряная и бронзовая медали?
Воспользуйтесь правилом умножения

Золотая медаль: 12 способов
Золотая и серебряная медаль:
12×11=132 способа
Золотая, серебряная и бронзовая медаль:
12×11×10=1320 способа

варианты переборы
правило умножения
способы перестановки
дерево возможных вариантов
Комбинаторика

16.03.2011г.
Домашнее задание
№ 1220
№1249
№1303