9-klass-kvadratichnaya-funkciya.ppt

Графики функций
у=ах2+n и у=а(х-m)2
Тема урока:
Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании
Аристотель

Устный опрос
Сформулировать определение квадратичной функции;
Что является графиком квадратичной функции?
Сформулировать свойства квадратичной функции у=ах2 при а>0, a<0.
Как из графика функции у=ах2 можно получить график функции у=ах2 + n; график функции у=а(х-m)2

Задание 1
Задание 2
ЗАДАНИЕ 3

Практическое выполнение задания в тетради
В одной системе координат построить графики функций в тетрадях:
А)у = 1/2 x2; y = 1/2x2 +4; y =1/2x2 -3;
Б)у=-1/3х2 , y = -1/3(x-2)2 , y = -1/3(x+3)2 ,

Задание 1
Построить в одной системе
координат графики функции
y=x2 , y=x2-5 и y=x2+5

Задание 2
Построить в одной системе
координат графики функций у=2х2, у=2(х-5)2, у=2(х+4)2

Задание 3
Построить в одной системе координат графики функций у=2х2 ,у= 2(х-5)2+3,
у=-2(х+4)2-5

Проверь себя
Задание 1
Задание 2
Задание 3

Вывод:
График функции у=ах2 +n является
параболой, которую можно получить из
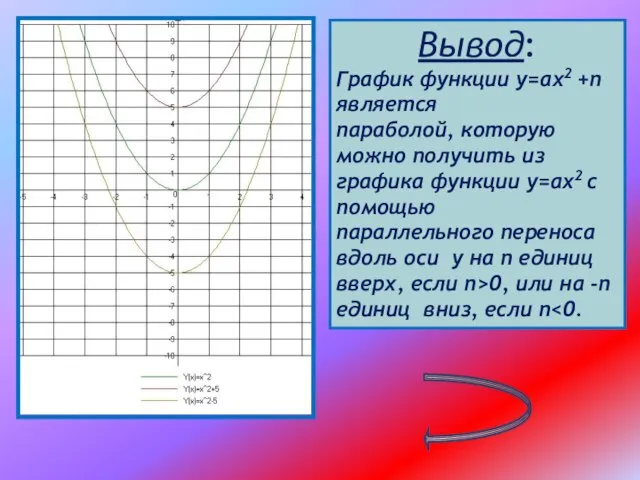
графика функции у=ах2 с помощью
параллельного переноса вдоль оси у на n единиц вверх, если n>0, или на -n единиц вниз, если n<0.

Вывод :
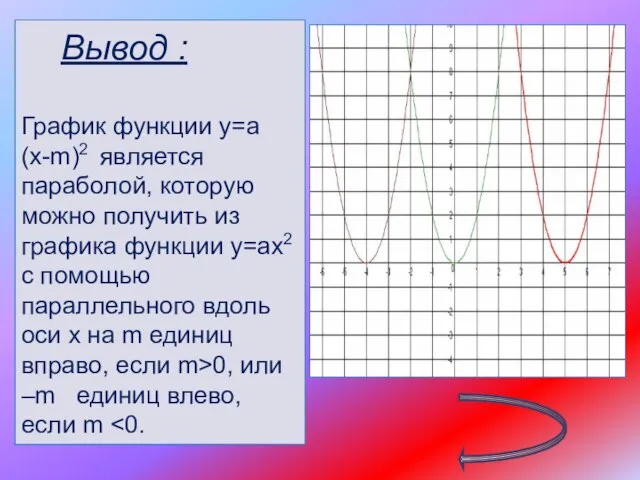
График функции у=а(х-m)2 является параболой, которую можно получить из графика функции у=ах2 с помощью параллельного вдоль оси х на m единиц вправо, если m>0, или –m единиц влево, если m <0.

Вывод:
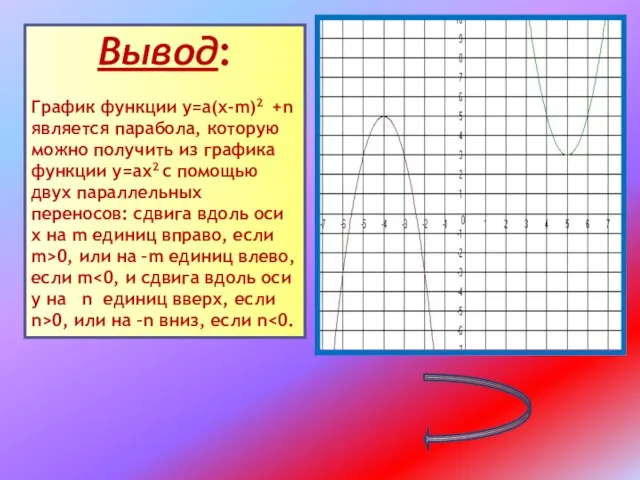
График функции у=а(х-m)2 +n является парабола, которую можно получить из графика функции у=ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m>0, или на –m единиц влево, если m<0, и сдвига вдоль оси у на n единиц вверх, если n>0, или на –n вниз, если n<0.