Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к

План
Различные подходы к определению понятия функция
Методика введения понятия функции в учебниках различных авторов
Методические особенности изучения отдельных классов функций.

Обоснование функциональной линии как ведущей для школьного курса математики — одно из крупнейших достижений современной методики.
Фундаментальность понятия порождает многообразие путей разворачивания содержания данной линии и различные трактовки самого понятия

Генетическая трактовка понятия «функция»
Генетическая трактовка понятия функции основана на понятиях
переменная величина,
функциональная зависимость переменных величин,
формула (выражающая одну переменную через некоторую комбинацию других переменных),
декартова система координат на плоскости.

Генетическая трактовка
понятия «функция»
Достоинства генетической трактовки:
«динамический» характер понятия функциональной зависимости,
легко выявляемый модельный аспект понятия функции относительно изучения явлений природы. ,
Легко устанавливаемая связь с остальным содержанием курса алгебры, поскольку большинство функций, используемых в нем, выражаются аналитически или таблично.

Генетическая трактовка
понятия «функция»
Недостатки генетической трактовки:
переменная при таком подходе всегда неявно (или даже явно) предполагается пробегающей непрерывный ряд числовых значений. Поэтому понятие связывается только с числовыми функциями одного числового аргумента

Логическая трактовка
понятия «функция»
Логическая трактовка понятия функции:
понятие функции выводится из понятия отношения,
функция выступает в виде отношения специального вида между двумя множествами

Логическая трактовка
понятия «функция»
Достоинства логической трактовки:
Обогащение языка школьной математики за счет иллюстрирования понятия с помощью разных средств;
Обобщенность понятия, позволяющая устанавливать различные связи.
Недостатки логической трактовки:
Выработанное понятие не востребовано, т.к. в дальнейшем в основном используются только числовые функции

В практике современной школы в качестве ведущего подхода принят генетический подход с одновременным использованием всего полезного из генетического подхода.

Система компонентов
понятия «функции»
представление о функциональной зависимости переменных величин в реальных процессах и в математике;
представление о функции как о соответствии;
построение и использование графиков функций, исследование функций;
вычисление значений функций, определенных различными способами.

Введение понятия функции — длительный процесс, завершающийся формированием представлений о всех компонентах этого понятия в их взаимной связи и о роли, играемой им в математике и в ее приложениях.
Изучение разных способов задания функции – важный методический прием.

Направления введения
понятия «функция»
упорядочение имеющихся представлений о функции, развертывание системы понятий, характерных для функциональной линии:
способы задания и общие свойства функций,
Графическое истолкование области определения, области значений, возрастания и т. д.;
глубокое изучение отдельных функций и их классов;
расширение области приложений алгебры за счет включения в нее идеи функции и разветвленной системы действий с функцией.

Особенности первого направления
Однозначности соответствия аргумента и определенного по нему значения функции отводится значительное место.
Для формирования понятия привлекаются различные способы задания функции, хотя в дальнейшем все способы задания функций играют соподчиненную роль аналитическому способу задания

Причины важности рассмотрения
разных способов задания функции
Во-первых, оно связано с практической потребностью:
и таблицы, и графики, как правило, служат для удобного в определенных обстоятельствах представления функции, имеющей аналитическую форму записи.
Во-вторых, оно важно для усвоения всего многообразия аспектов понятия функции:
формула выражает функцию лишь будучи включенной в соответствующую систему представлений и операций, а эта система такова, что различные компоненты понятия функции могут быть отображены наиболее естественно различными средствами.

Система заданий на установление связей между тремя основными способами задания функции (формулой, графиком, таблицей) включает
6 типов упражнений с изменением формы
3 типа с сохранением формы

Основные подходы
к введению понятия «функции»
Индуктивный подход
Изначально рассмотрение большого числа примеров, с помощью которых интуитивно выявляется суть понятия,
последующее более строгое определение основных понятий.
Дедуктивный подход
Изначально полное и сжатое изложение учебного материала, пусть даже малопонятного при первом прочтении,
дальнейшая углубленная проработка всех примеров, терминов и определений с помощью иллюстраций.

Изучение классов функций
Класс функций – множество функций, обладающих общностью аналитического способа задания (формулы) и исходящими из этого сходными особенностями графика, областей применения.
Для функций, входящих в класс, изучение идет в двух аспектах :
Изучение данной функции как члена класса;
Изучение свойств всего класса на примере типичной функции, входящей в класс.

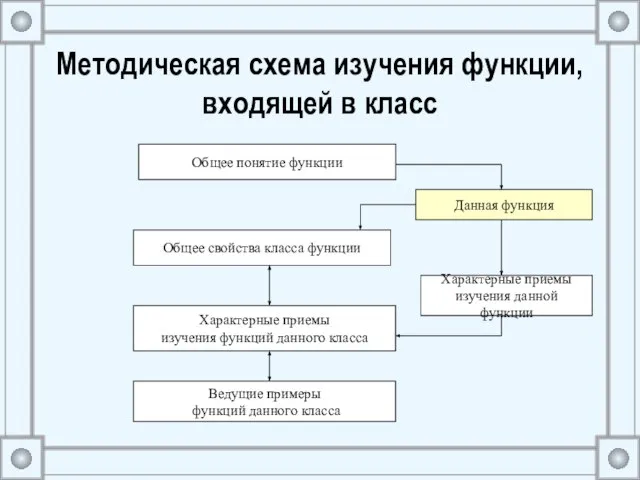
Методическая схема изучения функции, входящей в класс

Методические особенности изучения прямой и обратной
пропорциональной зависимости
Опора на знания о пропорции и пропорциональной зависимости величин.
Индуктивный подход к введению понятия.
Использование приема «загущения» точек при построении графика.

Последовательность действий
построения графиков функций методом «загустения» точек
нанесение нескольких точек;
наблюдение — все построенные точки расположены на одной прямой;
проведение этой прямой;
проверка:
берем произвольное значение аргумента и вычисляем по нему значение функции;
наносим точку на координатную плоскость — она принадлежит построенной прямой.
вывод о графике данной функции.

Изучение линейной функции
Представление о линейной функции выделяется при построении графика некоторой линейной функции.
Основная мысль, которую необходимо обосновать, состоит в том, что рассмотрение графика отдельно взятой линейной функции не может дать полного представления об основных свойствах графиков всех линейных функций.

Построение графиков
линейной функции
Построение первой из рассматриваемых функций проводится методом «загустения» точек.
Затем на основе вывода о виде линии, являющейся графиком любой линейной функции, геометрически обосновывается второй способ построения графика линейной функции – «по двум точкам».
Следует сразу отметить, что первый способ является универсальным (т.е. общим для всех функций), а второй – специфическим для линейной функции.

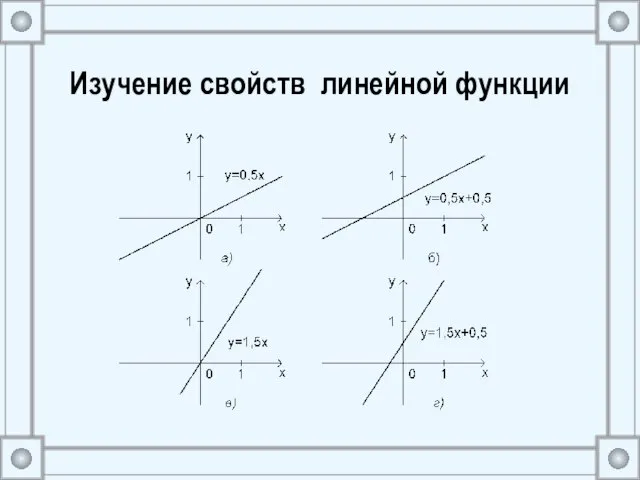
Изучение свойств линейной функции
Новая для учащихся познавательная задача
Исследовать класс функций у=kх+b в зависимости от параметров, установить геометрический смысл параметров.
Методический прием исследования:
Рассмотреть одновременно нескольких функций, у которых один из параметров изменяется, а другой остается постоянным.
Простейшая система, реализующая этот прием, состоит из четырех заданий с их последующим анализом и установлением связей между ними.

Изучение свойств линейной функции

Изучение свойств линейной функции
Графики (а) и (б) образуют с осью абсцисс одинаковые углы, это же имеет место и для графиков (в) и (г).
Графики (а) и (б) образуют с осью абсцисс меньшие углы, чем (в) и (г).
Коэффициенты при переменной в формуле для первой и второй функций одинаковы и меньше, чем соответствующие коэффициенты у третьей и четвертой функций.
Сформулировать вывод о зависимости рассмотренного угла от коэффициента.
Ввести термин «угловой коэффициент»

Изучение свойств линейной функции
Аналогичную работу необходимо провести для отрицательного коэффициента k и коэффициента b.
Рассмотренный прием называют
оценочным исследованием функции

Особенности изучения
квадратичной функции
Изучение квадратичной функции учащимися можно начать
с построения параболы,
с изучения физических процессов, где зависимость между величинами может быть выражена с помощью многочленов второй степени,

Особенности изучения
квадратичной функции
Для изучения квадратичной функции могут быть применены все приемы, использованные для изучения линейной функции:
построение графика методом «загустения» точек;
оценочное исследование функции.
Однако, для изучения свойств квадратичной функции этих приемов недостаточно, т.к. свойства квадратичной функции существенно отличаются от свойств линейной функции

Особенности изучения
квадратичной функции
Свойства квадратичной функции, требующие расширения приемов ее исследования и выполнения заданий особого вида:
функция не монотонна на области определения;
характер изменения функции не является равномерным;
ее график симметричен относительно некоторой прямой.

Особенности изучения
квадратичной функции
Главная особенность квадратичной функции: не все ее параметры имеют ясный геометрический смысл, как в случае с линейной функцией
Именно поэтому к изучению класса квадратичных функций привлекается прием, основанный на преобразовании выражения, задающего функцию, к виду y = а (х — b)2 + с, и использовании геометрических преобразований для построения графика произвольной квадратичной функции из параболы стандартного положения, т.е. графика функции у=ах2, а≠0.

Особенности изучения
квадратичной функции
Последовательность рассмотрения частных видов квадратичной функции:
y = х2,
y = ах2, а≠0.
y = ах2 + с, а≠0.
y = а(х + b)2, а≠0.
y = а(х + b)2 + c, а≠0.

Способы построение графиков
квадратичной функции
В результате всестороннего изучения свойств квадратичной функции и ее графиков должны быть сформированы два способа построения графика:
по характеристическим точкам;
с помощью преобразования графика простейшей функции y = х2,

Изучение степенной, показательной и логарифмической функций
Строится по аналогичным схемам.
Главной особенностью является
наличие больших ограничений на параметры.
ограничение области определения функций.

Изучение тригонометрических функций
Главное внимание уделяется свойствам четности/нечетности и периодичности функций;
Обобщаются все известные ранее приемы исследования функций и построения графиков;
Дальнейшее обобщение общие представления о свойствах функций и их графиков осуществляется в курсе начал математического анализа.