Содержание
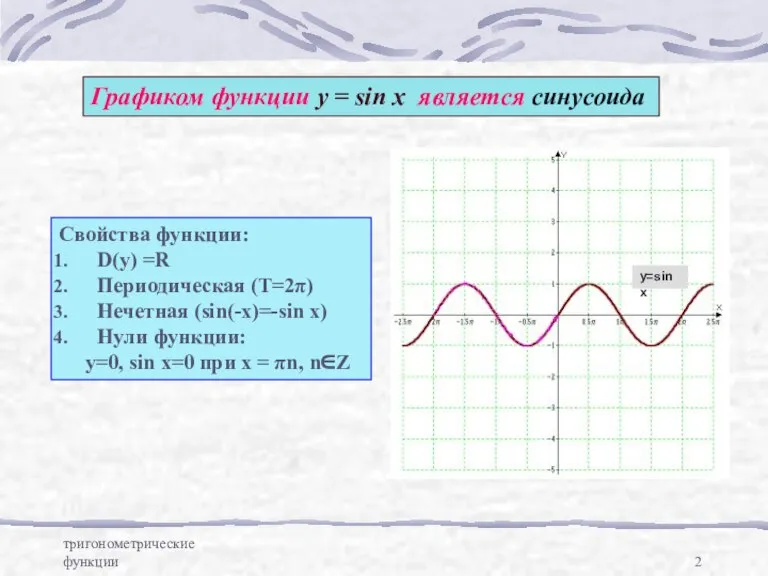
- 2. тригонометрические функции Графиком функции у = sin x является синусоида Свойства функции: D(y) =R Периодическая (Т=2π)
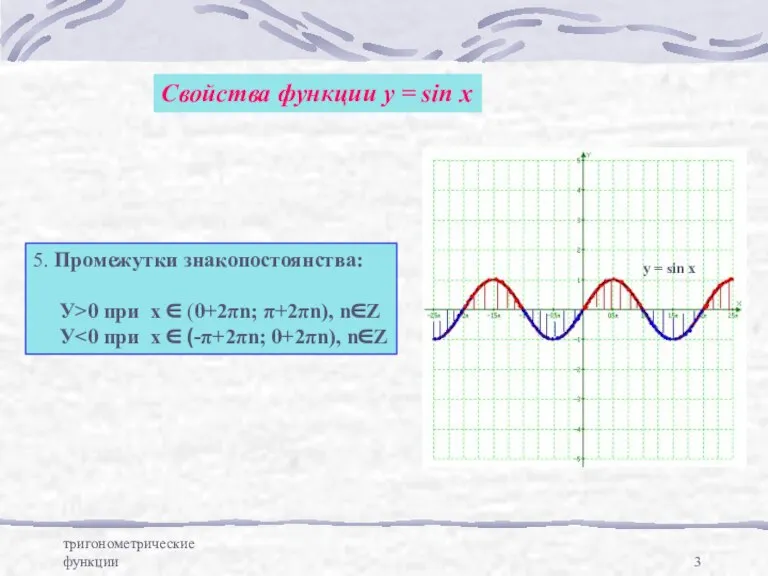
- 3. тригонометрические функции Свойства функции у = sin x 5. Промежутки знакопостоянства: У>0 при х ∈ (0+2πn;
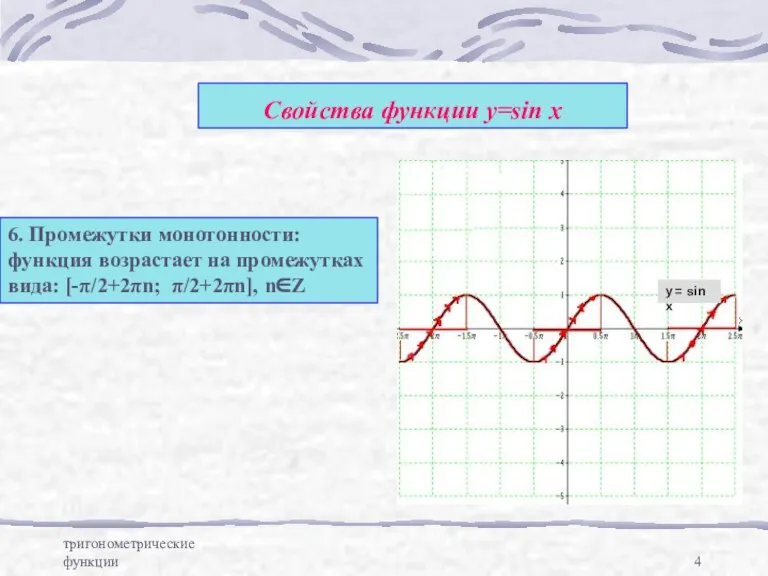
- 4. тригонометрические функции Свойства функции у=sin x 6. Промежутки монотонности: функция возрастает на промежутках вида: [-π/2+2πn; π/2+2πn],
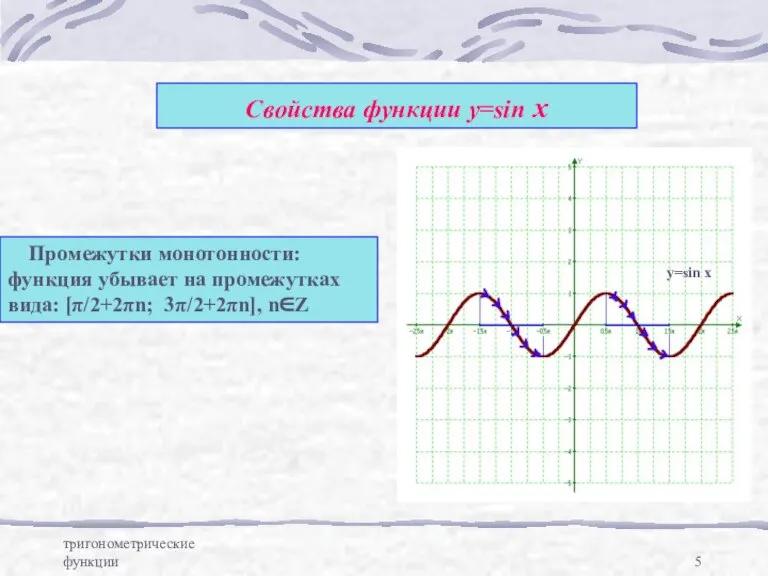
- 5. тригонометрические функции Свойства функции у=sin x Промежутки монотонности: функция убывает на промежутках вида: [π/2+2πn; 3π/2+2πn], n∈Z
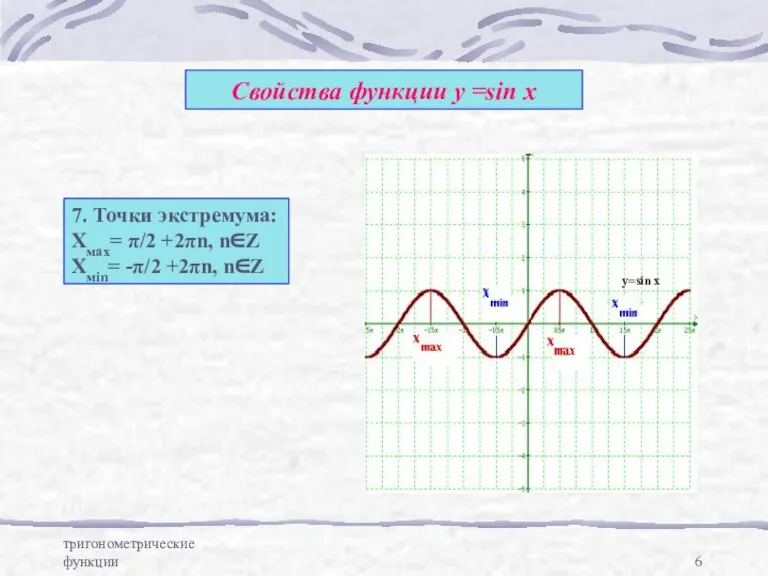
- 6. тригонометрические функции Свойства функции у =sin x 7. Точки экстремума: Хмах= π/2 +2πn, n∈Z Хмin= -π/2
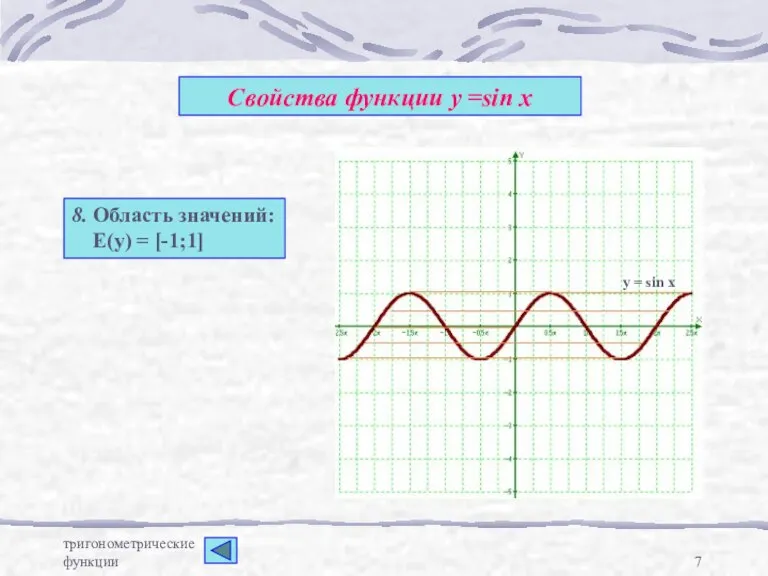
- 7. тригонометрические функции Свойства функции у =sin x 8. Область значений: Е(у) = [-1;1] y = sin
- 8. тригонометрические функции Преобразование графиков тригонометрических функций График функции у = f (x+в) получается из графика функции
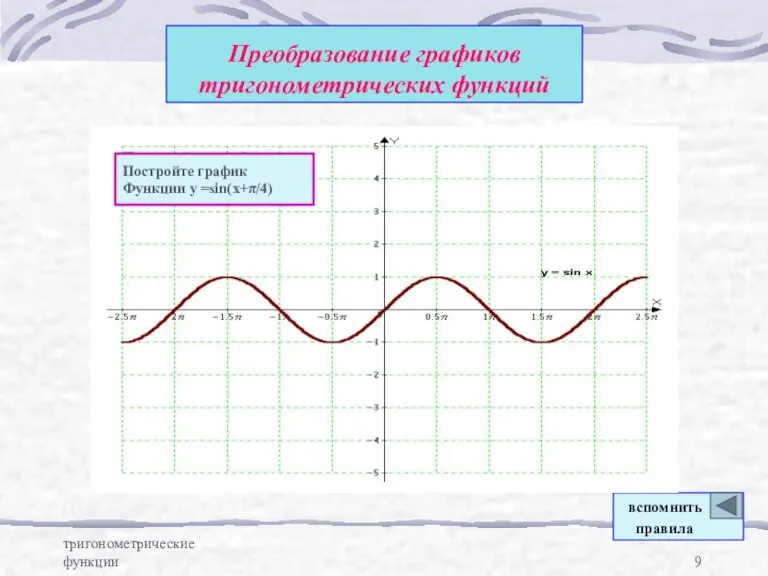
- 9. тригонометрические функции Преобразование графиков тригонометрических функций Постройте график Функции у =sin(x+π/4) вспомнить правила
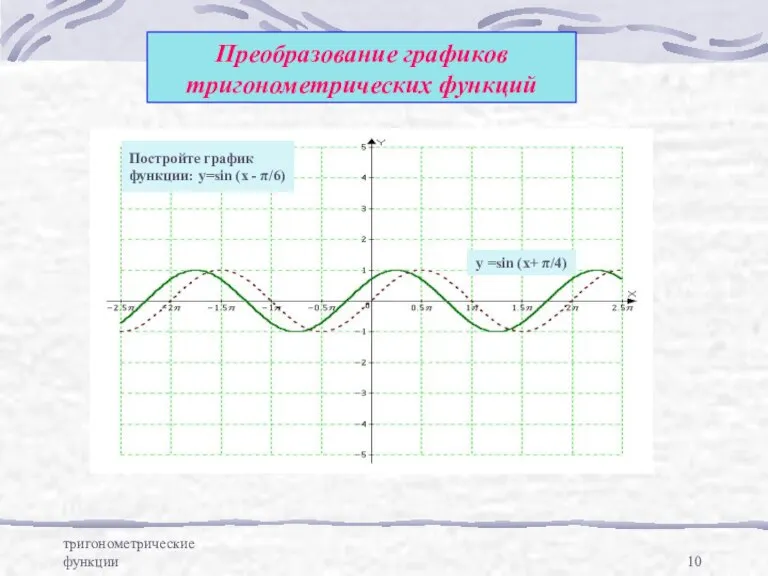
- 10. тригонометрические функции Преобразование графиков тригонометрических функций y =sin (x+ π/4) Постройте график функции: y=sin (x -
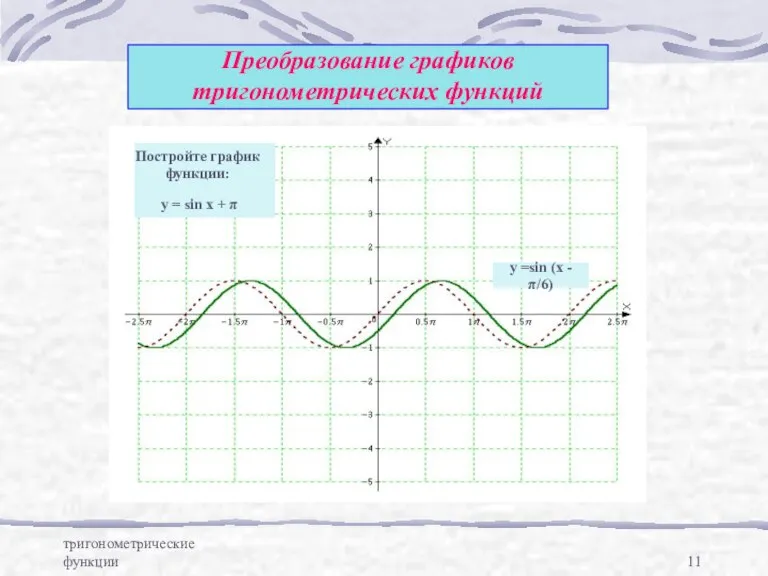
- 11. тригонометрические функции Преобразование графиков тригонометрических функций y = sin x + π Постройте график функции: y
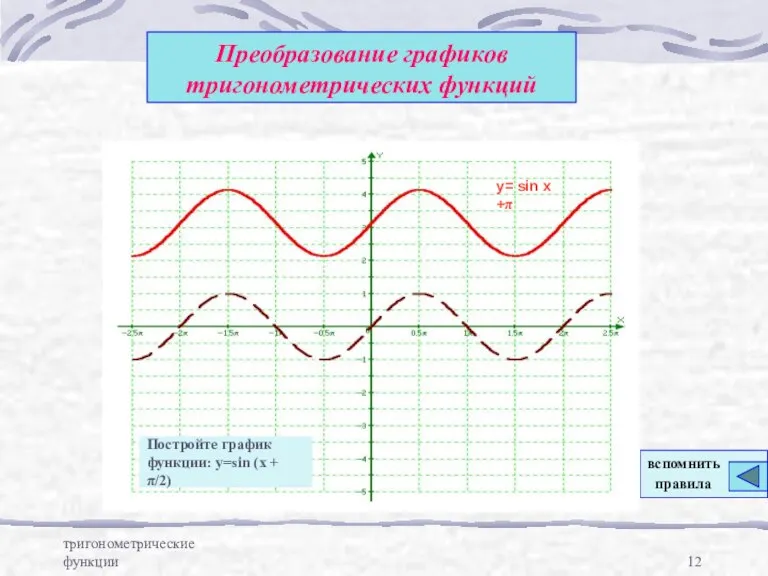
- 12. тригонометрические функции Преобразование графиков тригонометрических функций y= sin x +π Постройте график функции: y=sin (x +
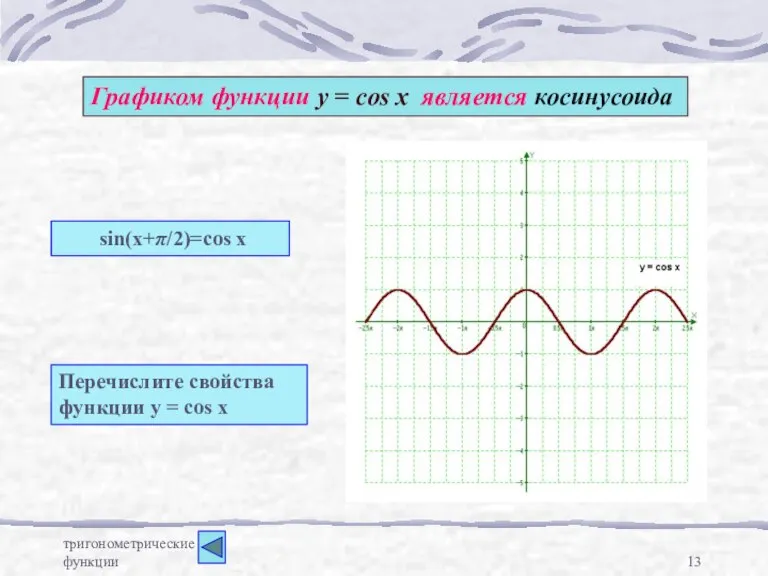
- 13. тригонометрические функции Графиком функции у = cos x является косинусоида Перечислите свойства функции у = cos
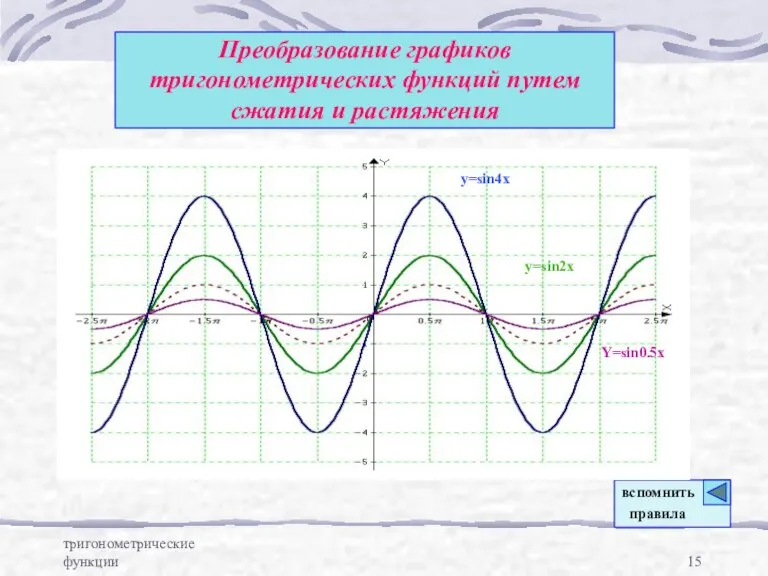
- 14. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у =k f (x)
- 15. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y=sin2x y=sin4x Y=sin0.5x вспомнить правила
- 16. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx)
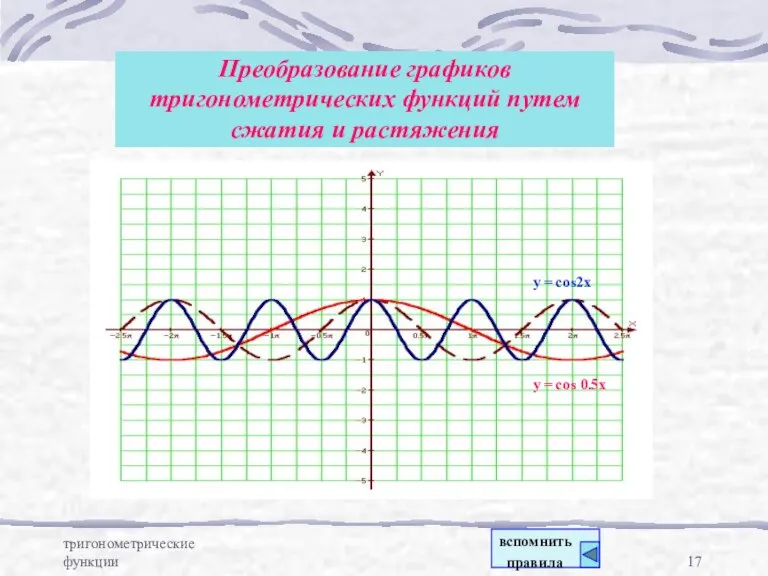
- 17. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y = cos2x y = cos
- 18. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения Графики функций у = -f (kx)
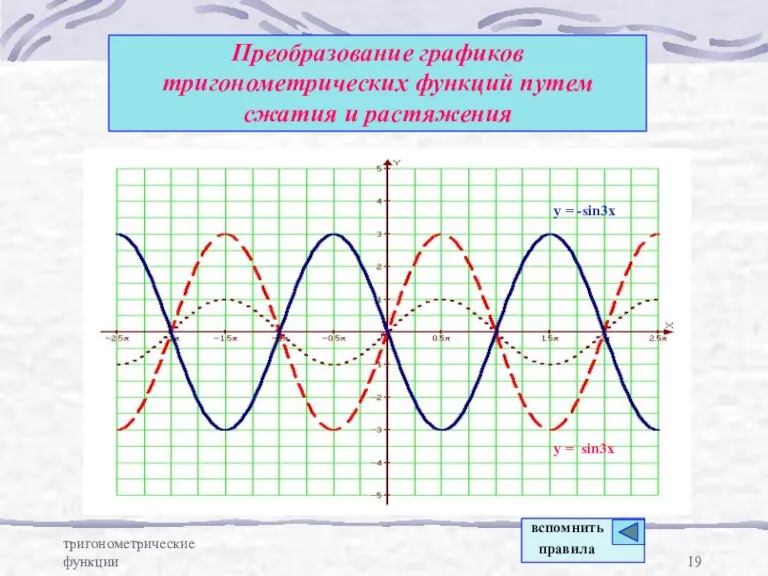
- 19. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y = -sin3x y = sin3x
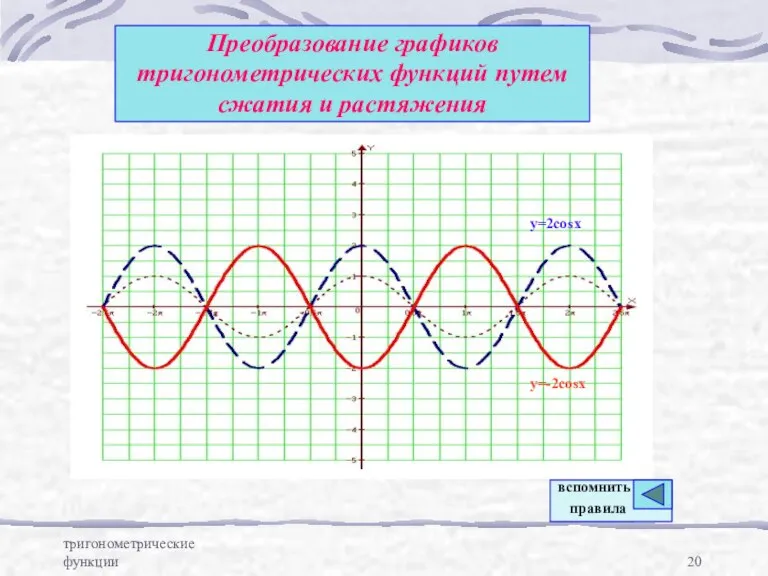
- 20. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения y=2cosx y=-2cosx вспомнить правила
- 21. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения График функции у = f (kx+b)
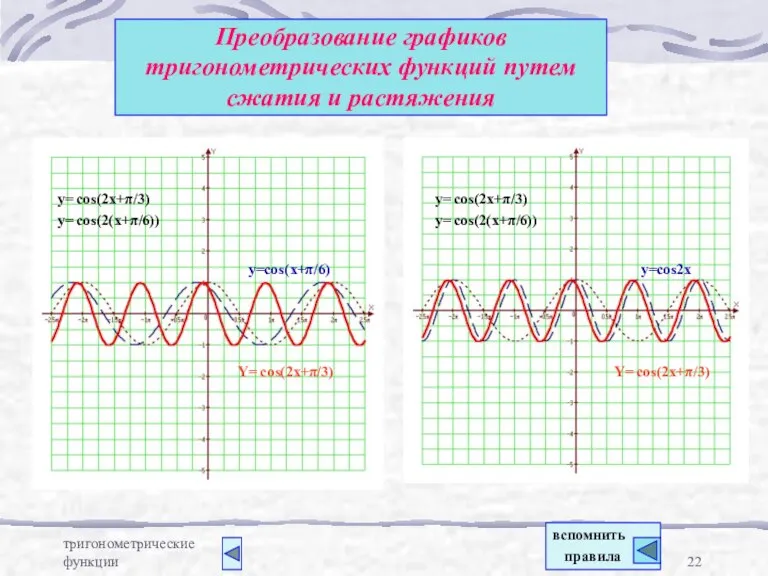
- 22. тригонометрические функции Преобразование графиков тригонометрических функций путем сжатия и растяжения Y= cos(2x+π/3) y=cos(x+π/6) y= cos(2x+π/3) y=
- 24. Скачать презентацию





 Функции. Графики функций 7 класс
Функции. Графики функций 7 класс Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.
Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.  ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ.
ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ. Что такое функция?
Что такое функция? Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей
Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Презентация на тему Научная революция 20 века
Презентация на тему Научная революция 20 века  Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Франсуа Виет 1540 - 1603
Франсуа Виет 1540 - 1603 Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3
Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3 Презентация на тему Буддизм
Презентация на тему Буддизм  Законы булевой алгебры
Законы булевой алгебры Логарифмы. Логарифмическая функция 10 класс
Логарифмы. Логарифмическая функция 10 класс Преобразования графиков функций 10 класс
Преобразования графиков функций 10 класс Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Виды показательных уравнений
Виды показательных уравнений  Алгебра логики. Понятие высказывания
Алгебра логики. Понятие высказывания Крестовые походы
Крестовые походы Тригонометрические уравнения
Тригонометрические уравнения  Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.
Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.  ГИА 2013 Модуль «АЛГЕБРА» №2
ГИА 2013 Модуль «АЛГЕБРА» №2 Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными Понятие бесконечной интегральной суммы. Интеграл
Понятие бесконечной интегральной суммы. Интеграл Алгебраическая дробь. Сокращение дробей
Алгебраическая дробь. Сокращение дробей Свойства функции Алгебра 9 класс
Свойства функции Алгебра 9 класс  Решение систем линейных уравнений с двумя неизвестными
Решение систем линейных уравнений с двумя неизвестными Свойства и график функции СИНУС
Свойства и график функции СИНУС