Содержание
- 2. ФРАНСУА ВИЕТ- Замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений
- 4. Рафаэль Бомбелли Профессор Сорбонны Рамус
- 5. Генрих III Генрих IV
- 6. Король Испании Филипп II
- 7. Герцог де Гиз
- 8. Ф. Виет «Введение в аналитическое искусство»
- 9. "In artem analyticen isazoge" (введение в анализ); "Ad logistica speciosum notae priores" (первые основания алгебраического исчисления,
- 10. «Все математики знали, что под алгеброй и алмукаболой…скрыты несравненные сокровища, но не умели их найти. Задачи,
- 11. А cubus + В рlanum in A3 aequatur D solito x3+Зbx=d
- 12. х1 + х2 = -b/a По праву достойна в стихах быть воспета О свойствах корней теоремы
- 13. Теорема косинусов А С В с b а a2 = b2 + c2 – 2bc x
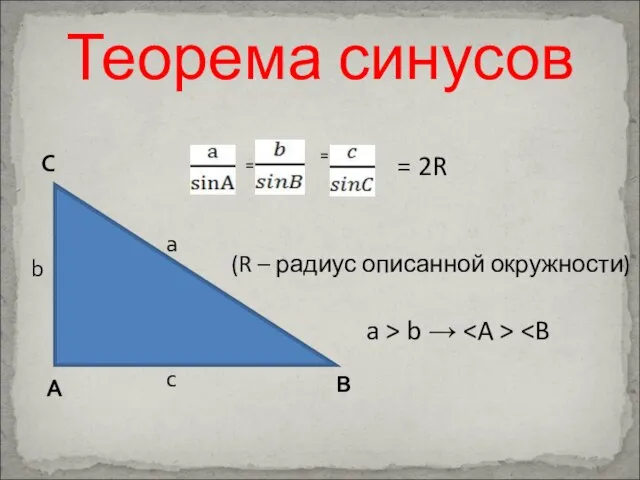
- 14. Теорема синусов С А В а b c = = (R – радиус описанной окружности) =
- 16. x45-(45x)43+(945x)41-(12300x)39+... +(95634x)5-(3795x)3+45x = a
- 17. Аполоний Пергский
- 18. «Искусство, которое я излагаю, ново или по крайней мере было настолько испорчено временем и искажено влиянием
- 19. ах2 + bх + с = 0 ах2 + bх = 0 ах2 + с =
- 21. Скачать презентацию
















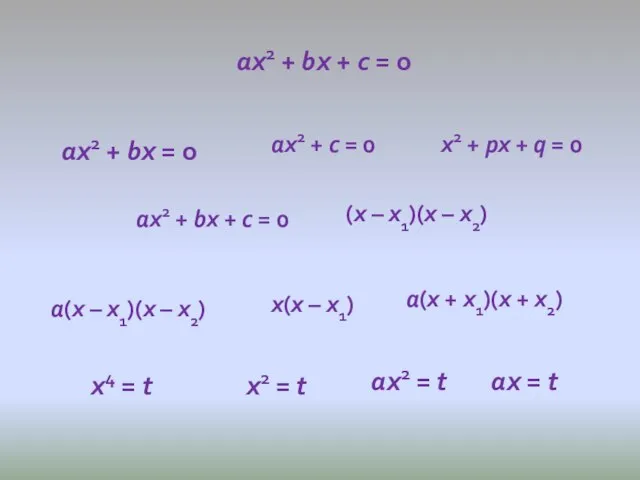
 Презентация на тему Понятие и задачи юридической психологии
Презентация на тему Понятие и задачи юридической психологии  Математика и естественные науки
Математика и естественные науки понятие вероятности (9класс)
понятие вероятности (9класс) Формула суммы первых n членов арифметической прогрессии
Формула суммы первых n членов арифметической прогрессии  математики и литература
математики и литература Закрепление основных разделов из курса «Алгебра и начала анализа. 10 – 11 класс»
Закрепление основных разделов из курса «Алгебра и начала анализа. 10 – 11 класс» Преобразование целых выражений
Преобразование целых выражений Решение неравенств с одной переменной 8 класс
Решение неравенств с одной переменной 8 класс Презентация на тему Основные теории местного самоуправления
Презентация на тему Основные теории местного самоуправления  ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук
ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук  Методы решения систем уравнений МОУ - СОШ №6 Учитель математики Миссюра Ирина Николаевна
Методы решения систем уравнений МОУ - СОШ №6 Учитель математики Миссюра Ирина Николаевна  Презентация на тему Собор святой Софии в Константинополе
Презентация на тему Собор святой Софии в Константинополе  Презентация на тему Современные модели развития науки
Презентация на тему Современные модели развития науки  Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.
Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.  Основные понятия, связанные с квадратными уравнениями
Основные понятия, связанные с квадратными уравнениями Функция y = k√x . Подкоренная функция
Функция y = k√x . Подкоренная функция Сумма «n» членов Арифметической прогрессии - презентация по Алгебре_
Сумма «n» членов Арифметической прогрессии - презентация по Алгебре_ zakony-algebry-logiki.pptx
zakony-algebry-logiki.pptx О числах
О числах Первообразная Правила нахождения первообразных
Первообразная Правила нахождения первообразных  ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков
ГРАФИЧЕСКОЕ РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ Урок формирования умений и навыков  Системы счисления
Системы счисления Франсуа Виет и его теорема
Франсуа Виет и его теорема Презентация на тему Роль теоцентризма в философиии средних веков
Презентация на тему Роль теоцентризма в философиии средних веков  Презентация на тему Система образования в Германии
Презентация на тему Система образования в Германии  Понятие бесконечной интегральной суммы. Интеграл
Понятие бесконечной интегральной суммы. Интеграл Решение простейших логарифмических логарифмических уравнений
Решение простейших логарифмических логарифмических уравнений Решение задач с помощью пропорций
Решение задач с помощью пропорций