Множества и операции над ними

МНОЖЕСТВО
ЭЛЕМЕНТ МНОЖЕСТВА
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ
ПОДМНОЖЕСТВО
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ВЫЧИТАНИЕ МНОЖЕСТВ
ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ
выход

Понятие множества — простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д.
Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.
МНОЖЕСТВО
Множество дней недели,
Множество месяцев в году
Множество точек на прямой,
Множество натуральных чисел

Элементы множества
Объекты, из которых образовано множество, называются элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c… z.
Если элемент х принадлежит множеству М, то записывают х О М, если не принадлежит – x П M
Если множество не содержит ни одного элемента, оно называется пустым и обозначается ∅ или 0.

Способы задания множеств
А = {3, 4, 5, 6}
Множество А двузначных чисел: свойство, которым обладает каждый элемент данного множества, - «быть двузначным числом».

Характеристическое свойство
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Этот способ задания множеств является общим и для конечных множеств, и для бесконечных.
«Множество А натуральных чисел, меньших 7»: А = {x | x ∈ N и x<7}

подмножество
Множество В является подмножеством множества А (В ⊂ А), если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.
Отношения между множествами наглядно представляют при помощи кругов Эйлера

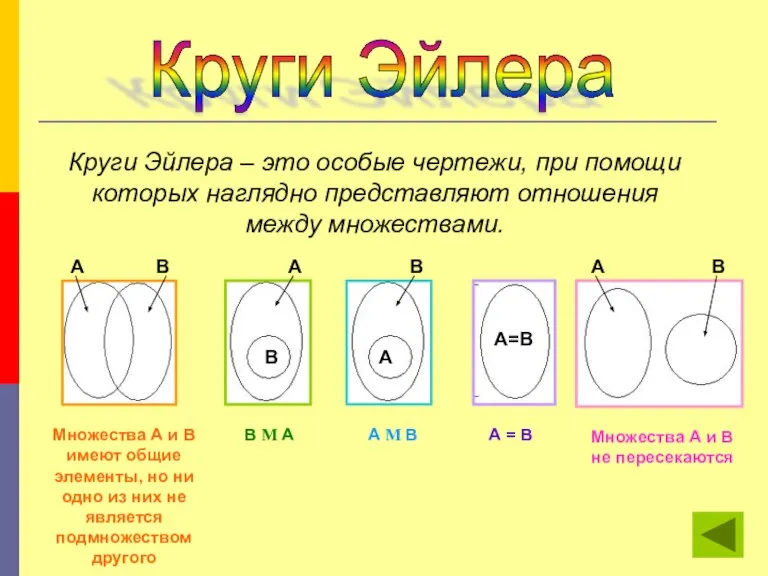
Круги Эйлера
Круги Эйлера – это особые чертежи, при помощи которых наглядно представляют отношения между множествами.
Множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого
В М А
А М В
А = В
Множества А и В не пересекаются
А
В
А
А
А
В
В
В
А=В

пересечение множеств
Пересечение множеств — множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. Пересечение множеств А и В обозначают А∩В.
Если множества А и В не имеют общих элементов, то пишут: А З В = Ж
Характеристическое свойство формулируется путем соединения характеристических свойств пересекаемых множеств союзом «и». Например, если А – множество четных натуральных чисел, а В – двузначных чисел, то элементы их пересечения обладают свойством: «быть четными натуральными и двузначными числами»
А∩В

Объединение множеств
Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В. Объединение множеств А и В обозначают А И В
А
В
Характеристическое свойство формулируется путем соединения характеристических свойств пересекаемых множеств союзом «или». Например, если А – множество четных натуральных чисел, а В – двузначных чисел, то элементы их объединения обладают свойством: «быть четными натуральными и двузначными числами»

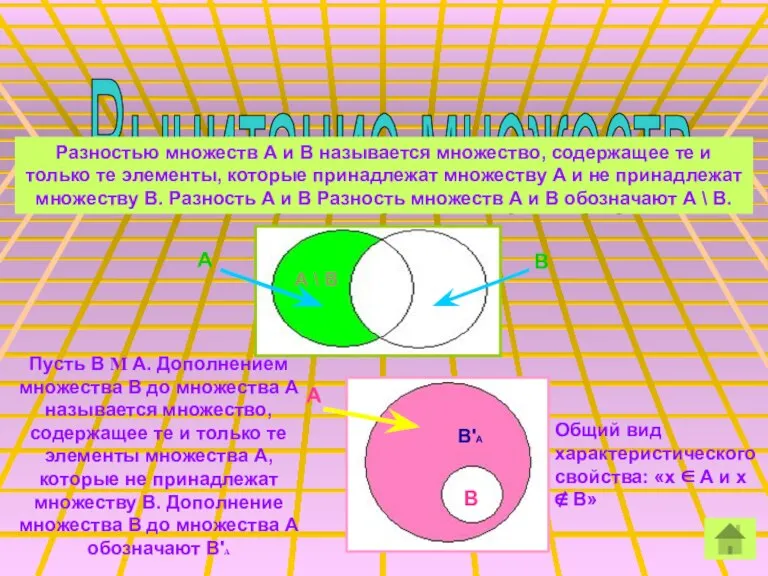
Вычитание множеств
Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. Разность А и В Разность множеств А и В обозначают А \ В.
А
В
А \ В
Пусть В М А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В. Дополнение множества В до множества А обозначают В'А
А
В
В'А
Общий вид характеристического свойства: «x ∈ А и x ∉ В»

Декартово произведение множеств
Декартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В. Декартово произведение обозначают А X В.
Операцию нахождения декартова произведения множеств называют декартовым умножением.
Если множества А и В конечны и содержат небольшое число элементов, можно изобразить декартово произведение этих множеств при помощи графа или таблицы.
Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости.

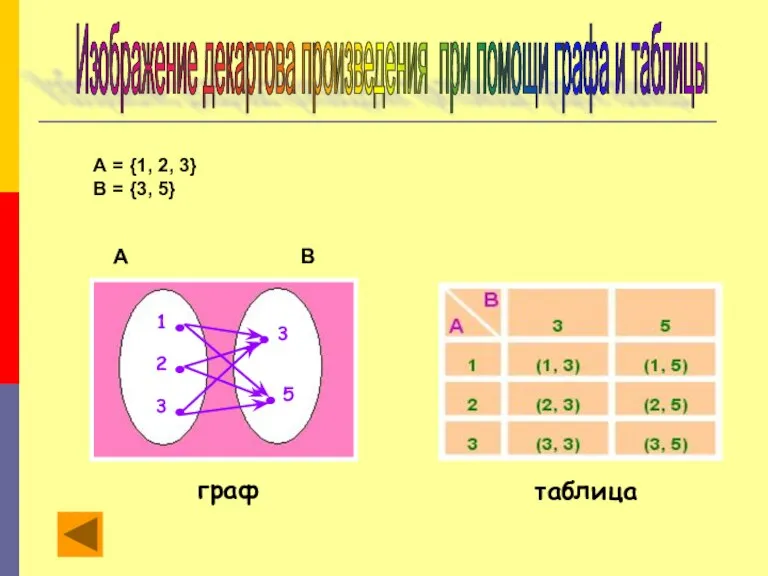
Изображение декартова произведения при помощи графа и таблицы
А = {1, 2, 3}
В = {3, 5}
А
В
1.
2.
3.
.3
.5
граф
таблица