Слайд 3
Из истории;
Понятие о производной;
Правила вычисления производной: -Основные правила дифференцирования, -Производная степенной

функции.
Производная сложной функции: -Сложная функция, -Производная триногометрических функций;
Применение.
Слайд 4Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи,

рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах.
Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др
Слайд 5Понятие о производной
Производной функции f в точке x0 называется число, к которому

стремится разностное отношение
∆f/Δx=f(x0+Δx)-f(x0)/Δx
при ΔX, стремящемся к нулю.
Слайд 6Основные правила дифференцирования
Правило №1. Если функции u и v дифференцируемыв точке x0,то

их сумма дифференцируема в этой точке (u+v)'= u'+v'.
Коротко говорят: производная суммы равна сумме производных.
Слайд 7Лемма. Если функция f дифференцируема в точке x0,то она непрерывна в этой

точке: ∆f→0 при ∆x→0, т.е.
f(x0+∆x )→(x0) при ∆x→0.
Слайд 8Правило №2. Если функции u и v дифференцируема в точке x0,то произведение

дифференцируемо в этой точке и (uv)'=u'v+uv'.
Слайд 9Следствие.Если функция u дифференцируема в точке x0,а С-постоянная, то функция Cu дифференцируема

в этой точке и (Cu)'=Cu'.
Коротко говорят: постоянный множитель можно выносить за знак проязводной.
Слайд 10Правило №3. Если функции u и v дифференцируемы в точке x0 и

функция v не равна нулю в этой точке, то частное u/v также дифференцируемо в x0 и
(u/v)'=u'v-uv'/v².
Слайд 11Производная степенной функции:
Для любого целого n и любого x (x≠0 при n≤1)

(xⁿ)'=nxⁿ־¹.
Слайд 12Целые рациональные функции (многочлены) и дробно-рациональные функции дифференцируемы в каждой точке своей

области определения.
Слайд 13Производная сложной функции:
Если функция f имеет производную в точке x0,а функция

g имеет производную в точке y0=f(x0), то сложная функция h(x)=g(f(x)) также имеет производную в точке x0 причём h'(x0)=g'(f(x0))·f '(x0).
Слайд 14Производные триногометрических функций:
Фориула производной синуса: Функция синус имеет производную в любой точке

и (sin x)'=cos x.
Слайд 15Формулы дифференцирования косинуса, тангенса и котангенса: функции y=cos x, y=tg x, y=ctg

x имеют производные вкаждой точке своей области определения,
и справедливы формулы:
(cos x)'=-sin x,
(tg x)'=1/cos² x,
(ctg x)'=-1/sin²x.
Слайд 16(sin x)'=cos x
(cos x)'=-sin x,
(tgx)'=1/cos² x,
(ctg x)'=-1/sin²x.
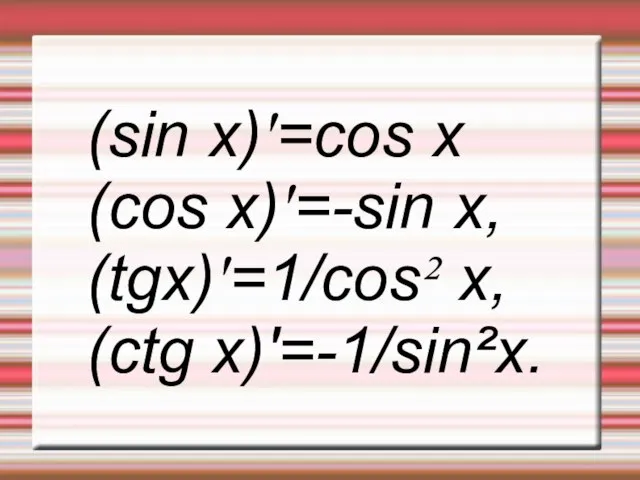
Слайд 17 Производные широко применимы в настоящее время, например, в экономическом анализе. Они

помогают точно вывести данные об изменении экономики государства. Используя их, можно совершенно точно просчитать, как можно увеличить доход государства и за счёт чего он может быть увеличен
Слайд 18Производная широко используется для исследования функций, т.е. для изучения различных свойств функций.

Например, с помощью производной можно находить промежутки возрастания и убывания функции, ее наибольшие и наименьшие значения.














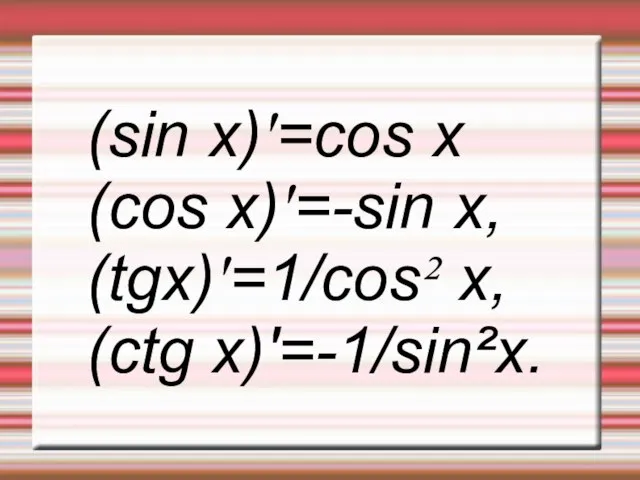


 Функции. Графики функций 7 класс
Функции. Графики функций 7 класс Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.
Краснооктябрьская средняя общеобразовательная школа, Республика Марий Эл Старикова Г.А., учитель высшей категории.  ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ.
ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ. Что такое функция?
Что такое функция? Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей
Презентация на тему Ответственность за несвоевременную или неправильную уплату таможенных платежей Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Презентация на тему Научная революция 20 века
Презентация на тему Научная революция 20 века  Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Франсуа Виет 1540 - 1603
Франсуа Виет 1540 - 1603 Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3
Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №3 Презентация на тему Буддизм
Презентация на тему Буддизм  Законы булевой алгебры
Законы булевой алгебры Логарифмы. Логарифмическая функция 10 класс
Логарифмы. Логарифмическая функция 10 класс Преобразования графиков функций 10 класс
Преобразования графиков функций 10 класс Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Виды показательных уравнений
Виды показательных уравнений  Алгебра логики. Понятие высказывания
Алгебра логики. Понятие высказывания Крестовые походы
Крестовые походы Тригонометрические уравнения
Тригонометрические уравнения  Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.
Урок в 11 классе. Урок в 11 классе. Составила учитель Кировской МБОУ Ткачук Н. П.  ГИА 2013 Модуль «АЛГЕБРА» №2
ГИА 2013 Модуль «АЛГЕБРА» №2 Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными Понятие бесконечной интегральной суммы. Интеграл
Понятие бесконечной интегральной суммы. Интеграл Алгебраическая дробь. Сокращение дробей
Алгебраическая дробь. Сокращение дробей Свойства функции Алгебра 9 класс
Свойства функции Алгебра 9 класс  Решение систем линейных уравнений с двумя неизвестными
Решение систем линейных уравнений с двумя неизвестными Свойства и график функции СИНУС
Свойства и график функции СИНУС