Содержание
- 2. Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова
- 3. Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b) называют любую ее первообразную функцию. Где
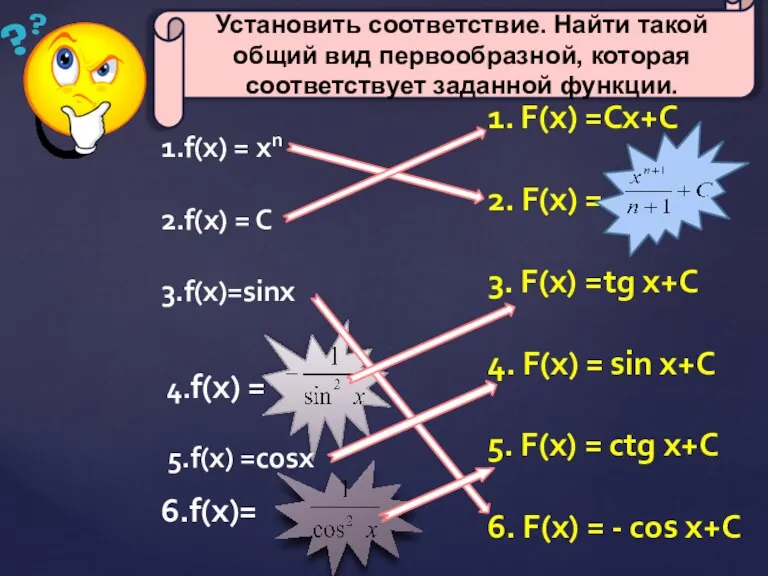
- 4. 1.f(x) = хn 2.f(x) = C 3.f(x)=sinx 4.f(x) = 6.f(x)= 1. F(x) =Сх+С 2. F(x) =
- 5. Свойства интеграла
- 6. Первообразная и неопределенный интеграл
- 7. Первообразная и неопределенный интеграл
- 8. Первообразная и неопределенный интеграл
- 9. Свойства интеграла
- 10. Таблица неопределенный интегралов
- 12. Свойства дифференциалов
- 13. Методы интегрирования
- 14. Интегрирование функций, содержащих квадратный трехчлен
- 15. Пример
- 30. Скачать презентацию








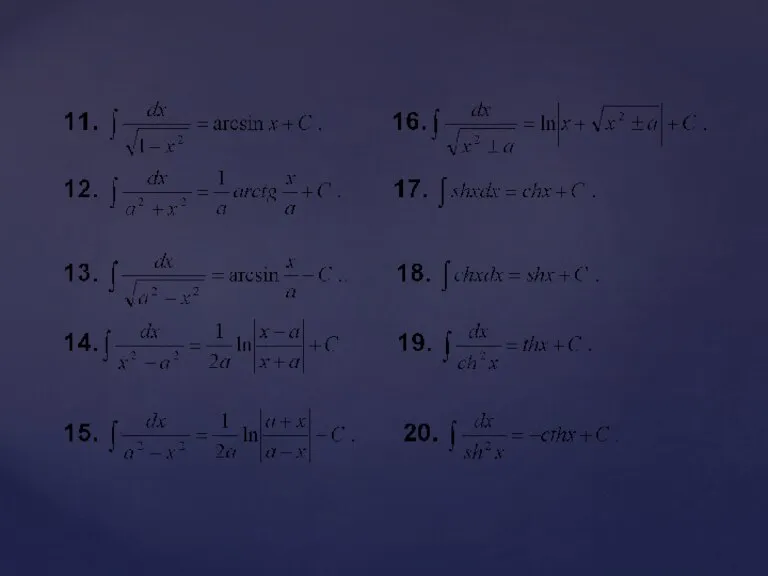

















 Франсуа Виет и его теорема
Франсуа Виет и его теорема Решение квадратных неравенств
Решение квадратных неравенств Тема урока: Теорема синусов
Тема урока: Теорема синусов  Primenenie-proizvodnoy-k-issledovaniyu-funkciy.ppt
Primenenie-proizvodnoy-k-issledovaniyu-funkciy.ppt Презентация на тему Основные проблемы применения коллизионного регулирования и способы их разрешения
Презентация на тему Основные проблемы применения коллизионного регулирования и способы их разрешения КВАДРАТНЫЙ КОРЕНЬ Дмитриева Ольга Евгеньевна учитель математики МБОУ «Большевсегодическая ООШ»
КВАДРАТНЫЙ КОРЕНЬ Дмитриева Ольга Евгеньевна учитель математики МБОУ «Большевсегодическая ООШ»  Решение линеиных неравенств - презентация по Алгебре_
Решение линеиных неравенств - презентация по Алгебре_ Презентация на тему Верование Восточных славян
Презентация на тему Верование Восточных славян  Математическая логика
Математическая логика Презентация на тему Иоганн Готфрид Гердер
Презентация на тему Иоганн Готфрид Гердер Применение производной
Применение производной Правила безопасности на воде
Правила безопасности на воде  Презентация на тему МАТРЁНА, МАТРЁША, МАТРЁШЕЧКА
Презентация на тему МАТРЁНА, МАТРЁША, МАТРЁШЕЧКА  Квадрат суммы. Квадрат разности
Квадрат суммы. Квадрат разности Презентация на тему Русская правда Ярослава Мудрого: свод законов древнерусского государства
Презентация на тему Русская правда Ярослава Мудрого: свод законов древнерусского государства  Понятие обратной функции. Определение логарифмической функции
Понятие обратной функции. Определение логарифмической функции Презентация на тему Дельфин Физминутка для глаз
Презентация на тему Дельфин Физминутка для глаз  Логарифмическая функция
Логарифмическая функция Линейная функция
Линейная функция  Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Презентация на тему Экономика стран Австралии и Океании
Презентация на тему Экономика стран Австралии и Океании  Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Классная работа. Пропорции. 11.01.13
Классная работа. Пропорции. 11.01.13 Презентация на тему Глубинная психология
Презентация на тему Глубинная психология  Предел переменной величины
Предел переменной величины Презентация на тему Протекционизм
Презентация на тему Протекционизм  Логарифмы
Логарифмы Способы задания функции
Способы задания функции