Слайд 2ТЕМА УРОКА
Как построить график функции y=f(x+L)+m, если известен график функции y=f

(x).
Слайд 3Цель урока:
Научиться строить график функции
y=f (x + L) +m.

Слайд 4Устная работа
Назовите координаты вершины параболы, направление её ветвей, уравнение оси симметрии:

а) y=x2 – 1; б) y=-2x2 + 5; в) y=(x-2)2; г) y=1/2(x+2)2.
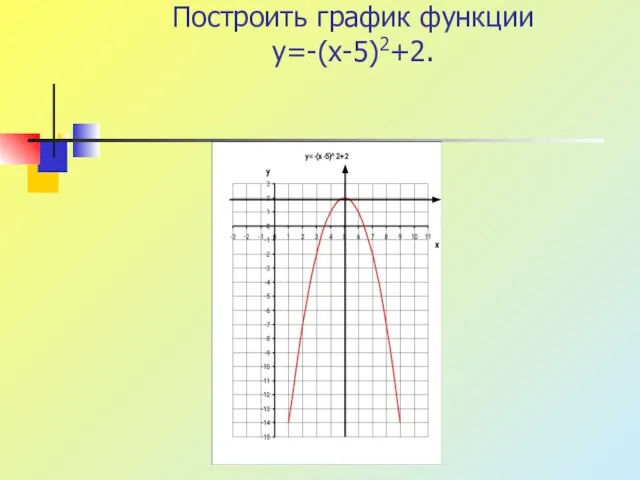
Слайд 7Построить график функции
y=-(x-5)2+2.
Слайд 8Алгоритм 1
1. Построить график функции y=f(x).
2. Осуществить параллельный перенос графика функции y=f(x)

вдоль оси x на l L l единиц масштаба влево, если L>0, и вправо, если L<0.
3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси y на l m l единиц масштаба вверх, если m>0, и вниз, если m<0.
Слайд 9Алгоритм 2
1.Перейдем к новой системе координат, проведя вспомогательные прямые x=-L, y=m (т.е.

выбрав началом новой системы точку(-L;m)).
2. В новой системе координат построить график функции y=f (x).
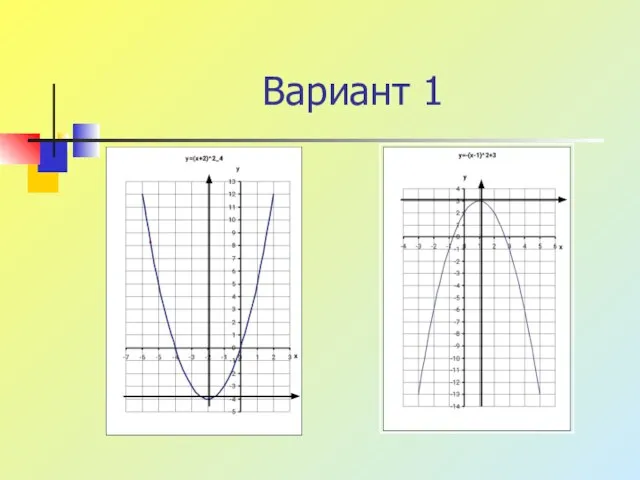
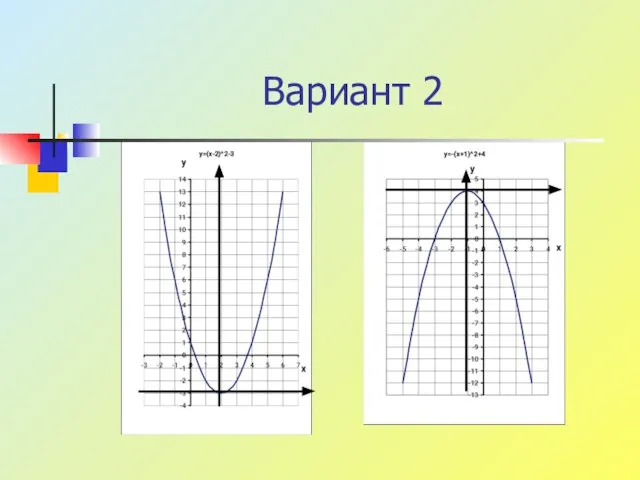
Слайд 10Самостоятельная работа
Вариант 1 Вариант 2
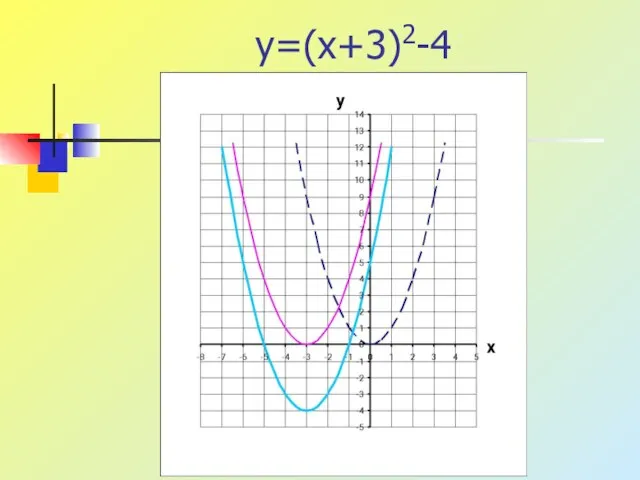
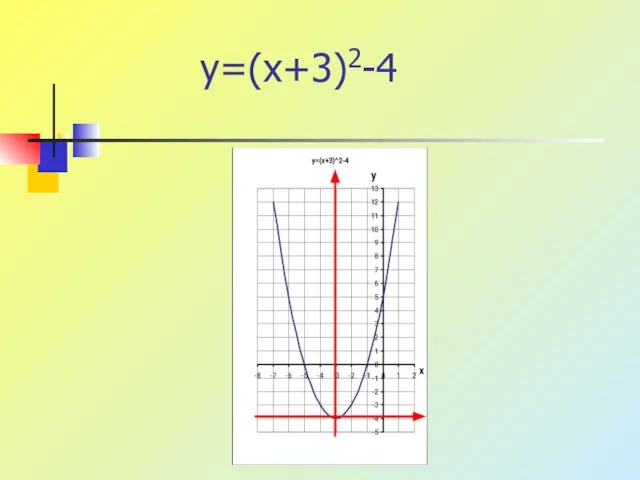
1. y=(x+2)2-4 1. y=(x-2)2-3
2. y=-(x-1)2+3 2. y=-(x+1)2+4

Слайд 139
8
7
6
5
4
3
2
1
-1
-2
-3
-10
-8
-6
-4
-2
2
4
6
8
у =
х
2
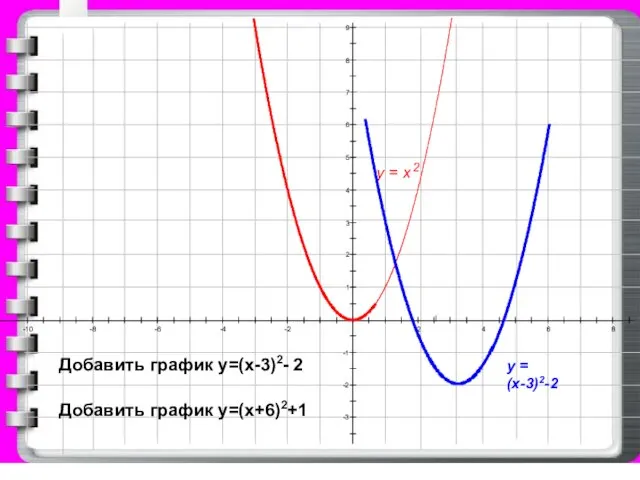
у = (х-3)2-2
Добавить график у=(х-3)2- 2
Добавить график у=(х+6)2+1
Слайд 149
8
7
6
5
4
3
2
1
-1
-2
-3
-10
-8
-6
-4
-2
2
4
6
8
у =
х
2
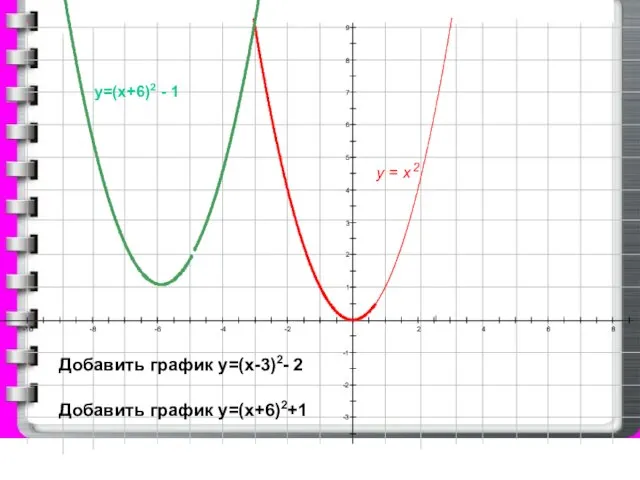
Добавить график у=(х-3)2- 2
Добавить график у=(х+6)2+1
у=(х+6)2 - 1
Слайд 159
8
7
6
5
4
3
2
1
-1
-2
-3
-10
-8
-6
-4
-2
2
4
6
8
у =
х
2
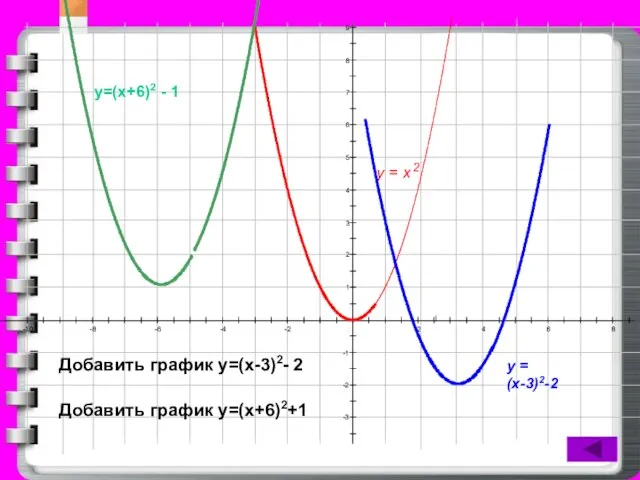
у = (х-3)2-2
Добавить график у=(х-3)2- 2
Добавить график у=(х+6)2+1
у=(х+6)2 - 1
Слайд 16g(x) = f(x) + a
Гg получается из Гf параллельным переносом на «a»
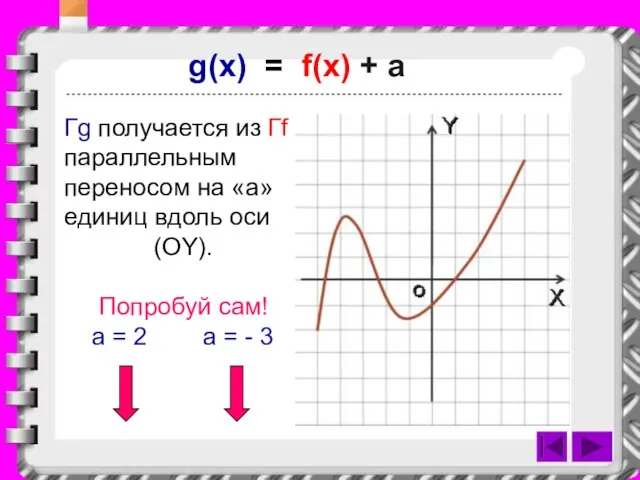
единиц вдоль оси
(OY).
Попробуй сам!
a = 2 a = - 3
Слайд 17g(x) = f(x) + a
Гg получается из Гf параллельным переносом на «a»
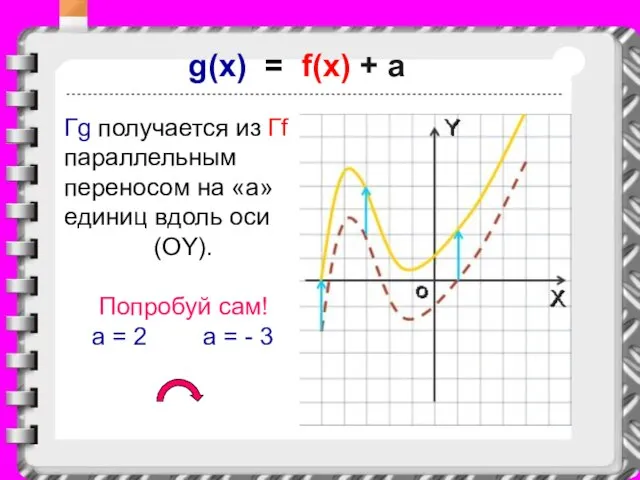
единиц вдоль оси
(OY).
Попробуй сам!
a = 2 a = - 3
Слайд 18g(x) = f(x) + a
Гg получается из Гf параллельным переносом на «a»
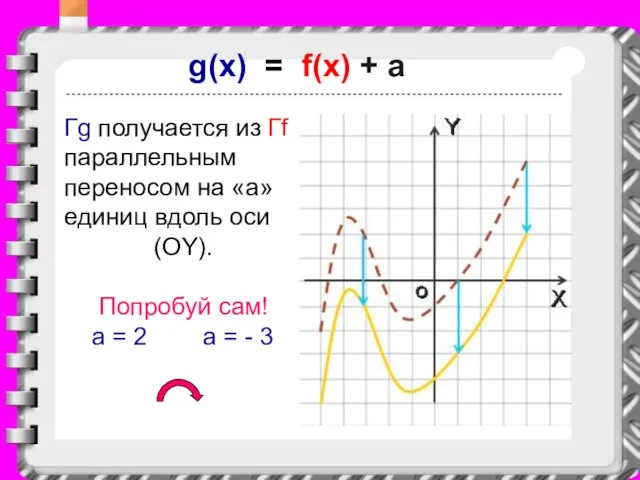
единиц вдоль оси
(OY).
Попробуй сам!
a = 2 a = - 3
Слайд 19g(x) = f(x + a)
Гg получается из Гf параллельным переносом на «-a»
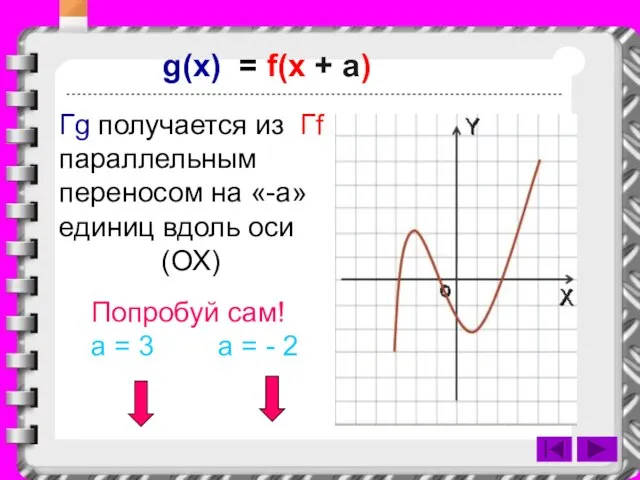
единиц вдоль оси
(ОХ)
Попробуй сам!
a = 3 a = - 2
Слайд 20g(x) = f(x + a)
Гg получается из Гf параллельным переносом на «-a»
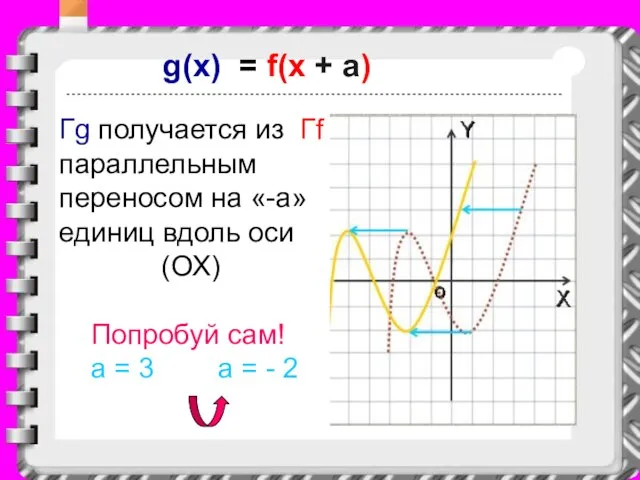
единиц вдоль оси
(ОХ)
Попробуй сам!
a = 3 a = - 2
Слайд 21g(x) = f(x + a)
Гg получается из Гf параллельным переносом на «-a»
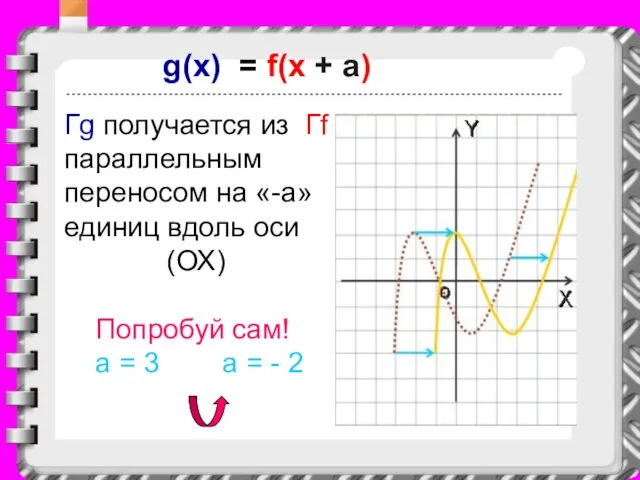
единиц вдоль оси
(ОХ)
Попробуй сам!
a = 3 a = - 2
Слайд 22Домашнее задание
§ 10
№ 10.36(в, г);
№ 10.41(а);
№ 10.35(а; б).


















 Разность квадратов
Разность квадратов Сложение чисел с разными знаками. 6 класс Новосёлова Е.А. МОУ «Усть-Мосихинская СОШ»
Сложение чисел с разными знаками. 6 класс Новосёлова Е.А. МОУ «Усть-Мосихинская СОШ» ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ.
ТЕМА УРОКА: РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ПО ФОРМУЛЕ. Презентация на тему Проблема интернализма и экстернализма в понимании механизмов научной деятельности
Презентация на тему Проблема интернализма и экстернализма в понимании механизмов научной деятельности  Одночлены и многочлены 7 класс
Одночлены и многочлены 7 класс Степенная функция (11 класс)
Степенная функция (11 класс) Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Действительные числа
Действительные числа Презентация на тему Суд в США
Презентация на тему Суд в США Неопределённый интеграл и методы его исчисления
Неопределённый интеграл и методы его исчисления Презентация на тему ОЩУЩЕНИЯ
Презентация на тему ОЩУЩЕНИЯ  Логарифмы. Применение логарифмов
Логарифмы. Применение логарифмов Lineynye-uravneniya-s-odnoy-peremennoy.pptx
Lineynye-uravneniya-s-odnoy-peremennoy.pptx Презентация на тему История развития юридической психологии
Презентация на тему История развития юридической психологии  Культурно-исторические рекреационные ресурсы Крыма
Культурно-исторические рекреационные ресурсы Крыма primenenie-proizvodnoy-funkcii.ppt
primenenie-proizvodnoy-funkcii.ppt Итоговое тестирование по алгебре 7 класс
Итоговое тестирование по алгебре 7 класс Применение производной
Применение производной Неравенства с двумя переменными
Неравенства с двумя переменными Способы задания последовательностей
Способы задания последовательностей  Методика обучения решению линейных неравенств с одной переменной
Методика обучения решению линейных неравенств с одной переменной Logarifmicheskaya-funkciya.ppt
Logarifmicheskaya-funkciya.ppt Квадратичная функция. функция
Квадратичная функция. функция  Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
Арифметическая прогрессия.Формула n –го члена арифметической прогрессии Алгебраические кривые в полярной системе координат и их применение в природе и технике
Алгебраические кривые в полярной системе координат и их применение в природе и технике Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Тригонометрические неравенства
Тригонометрические неравенства