Содержание
- 2. Необходимость решать уравнения не только первой, но и второй степени ёщё в древности была вызвана потребностью
- 3. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли
- 4. Франсуа Виет
- 5. Теорема Виета. Если приведенное квадратное уравнение x2+px+q=0 имеет действительные корни, то их сумма равна -p, а
- 6. Х2 – 14Х + 24 = 0 D=b2 – 4ac = 196 – 96 = 100
- 7. Х2 + 3Х – 10 = 0 Х1·Х2 = – 10, значит корни имеют разные знаки
- 8. Игра "Домино" Реши устно уравнения:
- 9. Определение квадратного уравнения. Квадратным уравнением называется уравнение вида ax2+bx+c=0, где x - переменная, a, b, c
- 10. Решение примера.
- 12. Скачать презентацию









 Формула суммы первых n членов арифметической прогрессии
Формула суммы первых n членов арифметической прогрессии  Обратные тригонометрические функции
Обратные тригонометрические функции ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук
ФОРМУЛЫ ПРИВЕДЕНИЯ Преподаватель ФГОУ СПО «СТК» Л.Г.Якимчук  Натуральные логарифмы
Натуральные логарифмы Teorema-Vieta.ppt
Teorema-Vieta.ppt Презентация на тему Монополии
Презентация на тему Монополии  О числах
О числах Производная (11 класс)
Производная (11 класс) Муниципальное общеобразовательное учреждение «Лермонтовская средняя общеобразовательная школа»
Муниципальное общеобразовательное учреждение «Лермонтовская средняя общеобразовательная школа» Методы решения квадратного уравнения
Методы решения квадратного уравнения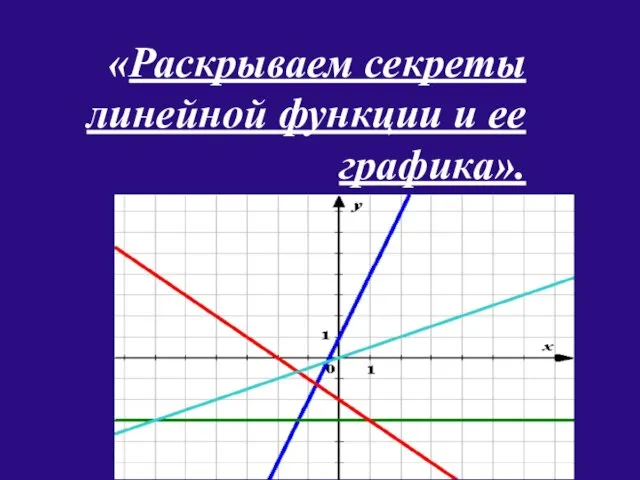 Раскрываем секреты линейной функции и ее графика - презентация по Алгебре_
Раскрываем секреты линейной функции и ее графика - презентация по Алгебре_ primenenie-proizvodnoy-funkcii.ppt
primenenie-proizvodnoy-funkcii.ppt Презентация на тему дефицит и профицит государственного бюджета
Презентация на тему дефицит и профицит государственного бюджета Определение линейной функции
Определение линейной функции Логарифмические неравенства
Логарифмические неравенства Сложение и вычитание обыкновенных дробей с одинаковым знаменателем
Сложение и вычитание обыкновенных дробей с одинаковым знаменателем Разность квадратов
Разность квадратов Действия с многочленами
Действия с многочленами Степень с целым показателем 8 класс
Степень с целым показателем 8 класс Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными Презентация на тему Государственный бюджет
Презентация на тему Государственный бюджет Презентация на тему Место муниципального права в российском праве
Презентация на тему Место муниципального права в российском праве  Решение неравенств с одной переменной
Решение неравенств с одной переменной 667
667 ВПК России 1
ВПК России 1 Применение неравенств и их свойств
Применение неравенств и их свойств Производная сложной функции
Производная сложной функции Применение производной для исследования функции
Применение производной для исследования функции