Применение квадратных уравнений для решения задач

Цели и задачи
Цель урока: Рассмотреть разные типы задач, приводящих к решению квадратных уравнений.
Задачи:
1) Обобщить знания и умения по данной теме.
2) Расширить связь математики с другими предметами и с жизнью.
3) Развивать творческие способности учащихся, внимание, стремление к знаниям, умение общаться.
4) Расширить кругозор учащихся в области истории математики.
5) Активизировать интерес к математики.

Творческие задания
Думай! Рассуждай! Решай!

Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.

«Ищи ошибку»
Ученик 8 класса решил два уравнения. Проверь решение и исправь ошибки.
1)х2 – x - 12 = 0
Решение: D = b2 – 4 ac
D = -12 - 4∙1∙(- 12) = - 49 нет корней

«Ищи ошибку»
-3 х2 +5 x +2 = 0
Решение: D = b2 – 4 ac
D = (-5)2 – 4∙3∙(- 2) = 25 - 24 = 1 , два корня
X1 =- 2/3 ; x2 = 1
Верные ответы: 1) х1 = 4 и х2 = -34;
2) х1 = 2 и х2 = - 1/3
2)

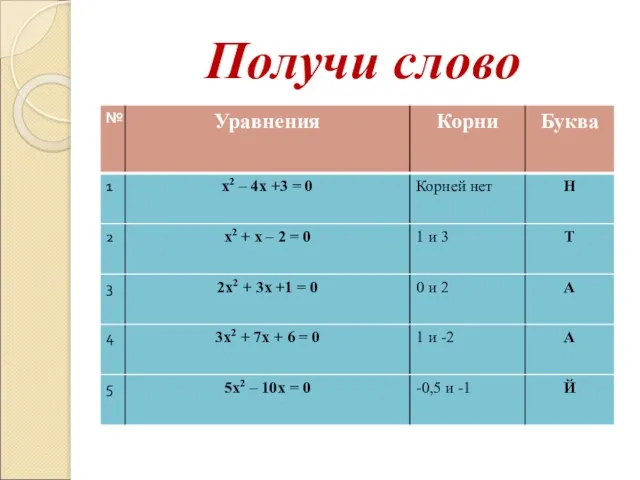
Получи слово

Тайна Пифагора
Была у Пифагора и его учеников тайна, сохраняемая под угрозой жизни. Рассмотрим квадрат АВСД со стороной 1 см. Проведём диагональ ВД. Найдём её длину. По теореме Пифагора квадрат гипотенузы ВД равен сумме квадратов катетов АВ и АД, квадрат ВД равен двум, ВД равно корню квадратному из двух. Сейчас мы знаем, что это иррациональное число. Но во времена Пифагора этого не знали.
Это противоречило утверждению Пифагора
« Всё есть число». Отрезок существует, а числа, выражающего его длину, нет. Пифагор
решил сохранить это своё открытие в тайне.

Чёрный ящик
Угадайте, что в ящике?
Один из основных органов растения.
Непроизвольная основа слова.
Число, которое после подстановки его в уравнение, обращает уравнение в тождество.
(корень)
Решите уравнения и вы
узнаете какому растению принадлежит корень.
1) х² - 8х + 15 = 0; 2) х² - 5х – 6 = 0
3) х² - 11х +18 = 0; 4) 3х² +4х + 20 = 0
Ключ: 5,3 – р; 6,-1 – о; 9,2 –з; корней нет - а

Р о з а
О розе существует интересная легенда: по словам Анакреона, родилась роза из белоснежной пены, покрывающей тело Афродиты, когда богиня любви выходила из моря. Поначалу роза была белой, но от капельки крови богини, уколовшейся о шип, стала алой.

Ряд Рачинского – 10, 11, 12, 13, 14.
10² + 11² +12² = 13² +14²
Задание: Единственный ли это ряд из пяти последовательных чисел, у которых сумма квадратов первых трёх равна сумме квадратов двух последних.
Решение: обозначим пять последовательных чисел так:
х– 1, х, х + 1, х +2, х +3.
Тогда:(х – 1)² + х² + (х + 1)² = (х +2)² + (х +3)²;
Х² - 2х + 1 + х² + х² + 2х + 1 = х² + 4х +4 + х² + 6х + 9;
Х² - 10х – 11 = 0;
Д = 144;
Х =11; или х = -1.
Следовательно, существует два ряда чисел, с таким свойством:
10, 11,12,13 и -2, -1, 0, 1, 2

Современная мастерская
Задание: Можно ли из круглого листа железа, диаметром 1, 4 метра, вырезать прямоугольник со сторонами, равными корням уравнения:
0,1х2 – 0,2х + 0,1 = 0.
Решение: Перейдём к равносильному уравнению: х2 – 2х + 1 = 0. (х – 1)2 = 0. Х = 1. Значит надо вырезать квадрат со стороной 1 метр.
1Способ: а2 = 0.72 + 0.72 = 0,98; а = 0, 7 √2 ˂ 1
2Способ: а = 2R*sin45º = 0,7 √2
Ответ: Нет.

«Дорога жизни»
«Дорогой жизни» стало Ладожское озеро. 22 ноября 1941 года по всё ещё неокрепшему льду прошла 1-я автомобильная колонна в блокадный Ленинград из 60 грузовых машин, где лежали мешки с мукой и другие продукты. А из Ленинграда вывозили обессиленных от голода женщин и детей.

Задача
С какой скоростью по ещё неокрепшему льду Ладоги двигались грузовые машины и лошадиные повозки, если расстояние около 30 км машина проходила на 1 час быстрее, чем повозка, так как скорость машины на 5 км/час больше?

Решение задачи
Пусть х км/час – скорость повозки.
(х + 5) км/час – скорость машины.
Уравнение:
30/х – 30/(х + 5) = 1
х² + 5х – 150 = 0
х = 10 и х = -15
Ответ: 10 км/час и 15 км/час.

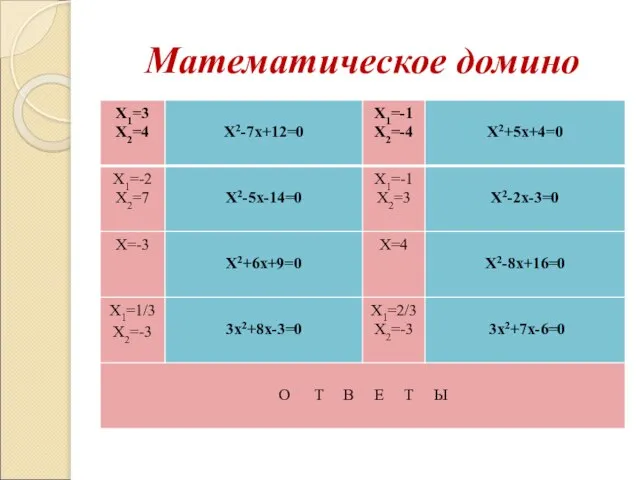
Математическое домино