Применение производной для исследования функций. 1. Нахождение промежутков возрастания функции. 2. Нахождение промежутков убыв

Монотонность функции
Убывает на
(-∞;x1], [x2;+∞)
Возрастает на
[х1; х2].
Постоянна на
[а;в]
у
х
У=f(x)
x1
х2
а
в

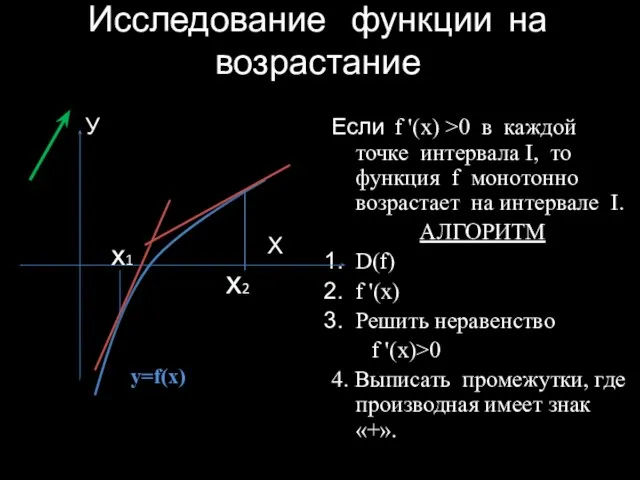
Исследование функции на возрастание
У
Х
Если f '(x) >0 в каждой точке интервала I, то функция f монотонно возрастает на интервале I.
АЛГОРИТМ
D(f)
f '(x)
Решить неравенство
f '(x)>0
4. Выписать промежутки, где производная имеет знак «+».
у=f(x)
х2
х1

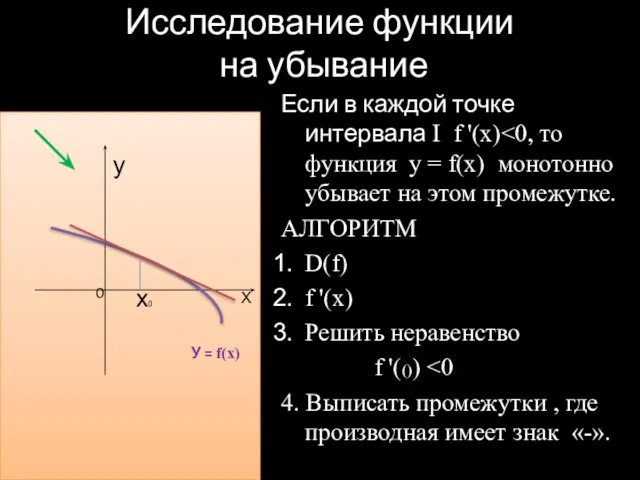
Исследование функции
на убывание
у
Если в каждой точке интервала I f '(x)<0, то функция у = f(x) монотонно убывает на этом промежутке.
АЛГОРИТМ
D(f)
f '(x)
Решить неравенство
f '(()) <0
4. Выписать промежутки , где производная имеет знак «-».
Х
0
х0
У = f(x)

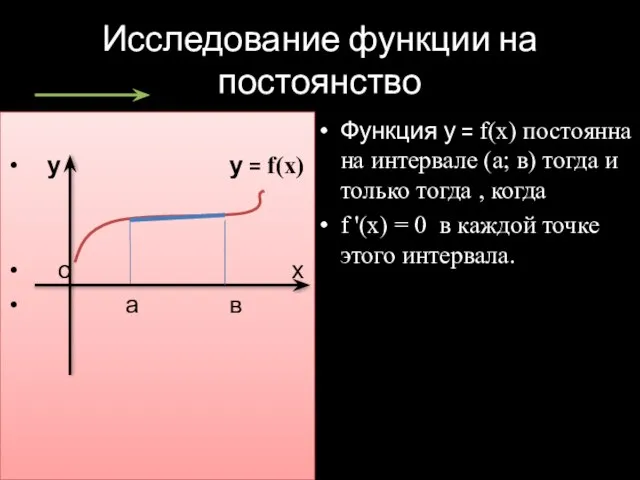
Исследование функции на постоянство
у у = f(x)
о х
а в
Функция у = f(x) постоянна на интервале (а; в) тогда и только тогда , когда
f '(x) = 0 в каждой точке этого интервала.

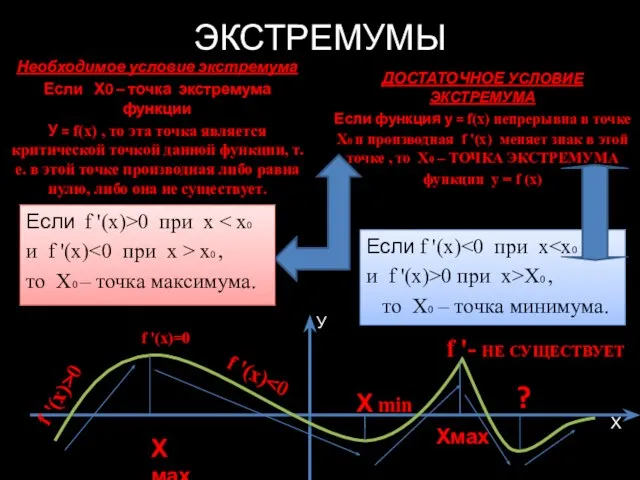
ЭКСТРЕМУМЫ
Необходимое условие экстремума
Если Х0 – точка экстремума функции
У = f(x) , то эта точка является критической точкой данной функции, т.е. в этой точке производная либо равна нулю, либо она не существует.
Если f '(x)>0 при х < x0
и f '(x)<0 при х > x0 ,
то Х0 – точка максимума.
ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА
Если функция у = f(x) непрерывна в точке
Х0 и производная f '(x) меняет знак в этой точке , то Х0 – ТОЧКА ЭКСТРЕМУМА
функции у = f (x)
Если f '(x)<0 при х
и f '(x)>0 при x>Х0 ,
то Х0 – точка минимума.
f '(x)>0
f '(x)=0
f '(x)<0
Х мах
Х min
f '- НЕ СУЩЕСТВУЕТ
Хмах
У
Х
?

СХЕМА ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ ИНТЕРВАЛОВ МОНОТОННОСТИ И ЭКСТРЕМУМОВ
Характер изменения функции
- 2
3
+
-
+

А с и м п т о т ы
Прямая у = кх +в называется асимптотой графика функции у = f(x) , если расстояние от точки М графика функции до прямой
у = кх + в стремиться к нулю при бесконечном удалении точки М.
Прямая х = а является вертикальной асимптотой графика функции
у = f(x), если lim f(x) = ∞
х→ а
Прямая у = в является горизонтальной асимптотой графика функции у = f(x), если
lim f(x)=b
х→∞
Прямая у = кх + в является наклонной асимптотой графика функции у = f(x), если lim f(x) =к
х →∞ х
lim ( f(x)─kx ) = b
Х→∞
х
У у = в
У= f(x)
у
0
а
Х = а
М.
.М
0 Х
У = f(x)
. М
у = кх + в
y=f(x)
У
0
Х

СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
И ПОСТРОЕНИЕ ЕЁ ГРАФИКА.
НАХОЖДЕНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ И ОБЛАСТИ ЗНАЧЕНИЙ ФУНКЦИИ.
ИССЛЕДОВАНИЕ ФУНКЦИИ НА ЧЕТНОСТЬ И НЕЧЕТНОСТЬ.
ИССЛЕДОВАНИЕ ФУНКЦИИ НА ПЕРИОДИЧНОСТЬ.
ОПРЕДЕЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ГРАФИКА ФУНКЦИИ С ОСЯМИ КООРДИНАТ И ИНТЕРВАЛОВ, ГДЕ ФУНКЦИЯ СОХРАНЯЕТ ЗНАК.
НАХОЖДЕНИЕ АСИМПТОТ ГРАФИКА ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ ТОЧЕК ЭКСТРЕМУМОВ ФУНКЦИИ.
ПОСТРОЕНИЕ ГРАФИКА.

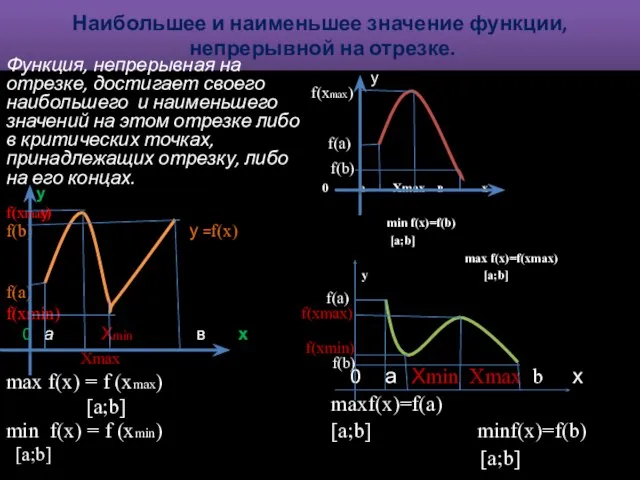
Наибольшее и наименьшее значение функции,
непрерывной на отрезке.
Функция, непрерывная на отрезке, достигает своего наибольшего и наименьшего значений на этом отрезке либо в критических точках, принадлежащих отрезку, либо на его концах.
f(b) у =f(x)
f(a)
f(xmin)
0 а Хmin в х
Хmax
maх f(x) = f (xmax)
[a;b]
min f(x) = f (xmin)
[a;b]
0 а Хmax в х
min f(x)=f(b)
[a;b]
max f(x)=f(xmax)
у [а;b]
0 а Хmin Хmax b х
maxf(x)=f(a)
[а;b] minf(x)=f(b)
[a;b]
у
f(xmax)
у
f(b)
f(a)
f(xmax)
у
f(a)
f(xmax)
f(xmin)
f(b)