Радианная мера углов и дуг

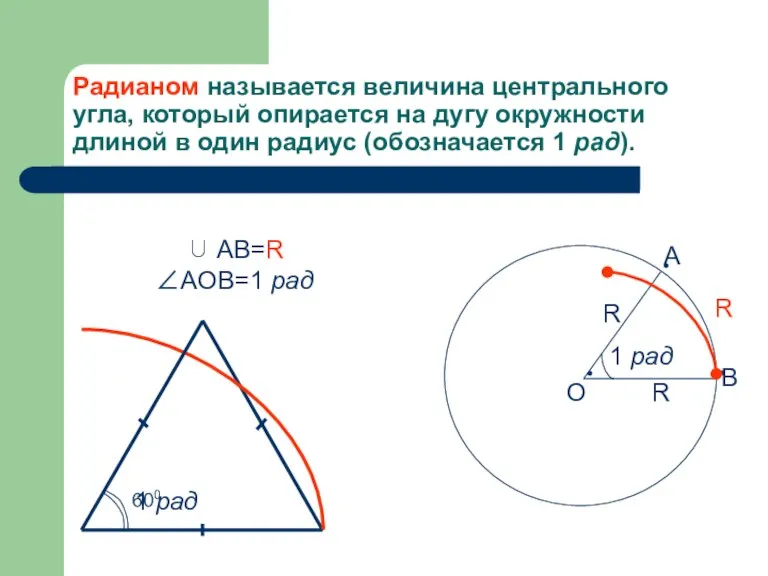
Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1 рад).
1 рад
R
R
R
A
B
O
⋅
⋅
⋅
∪ AB=R
∠AOB=1 рад
600
1 рад

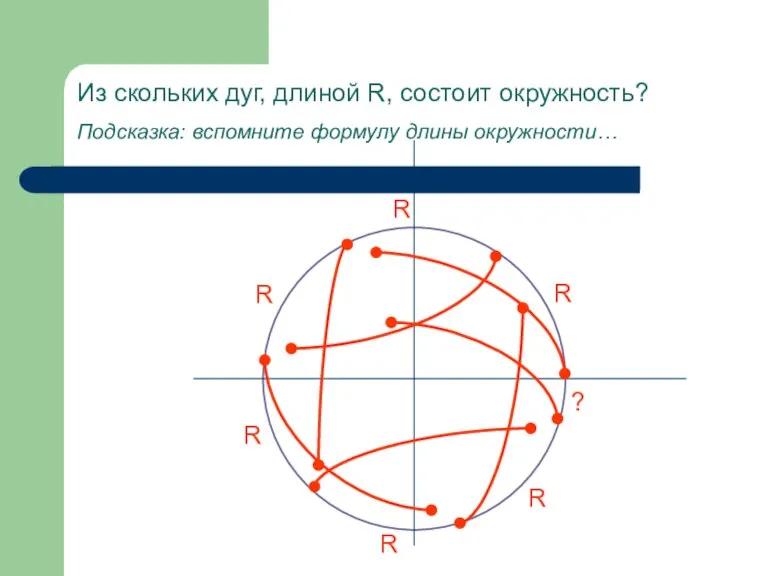
Из скольких дуг, длиной R, состоит окружность?
Подсказка: вспомните формулу длины окружности…
R
R
R
R
R
R
?

Задание 1. Вывести правила перевода из радианной меры в градусную и наоборот.
Ответ: α0= α0· рад − правило перевода из градусной меры в радианную;
α рад= α· − правило перевода из радианной меры в градусную.
1 рад = ; 1 рад ≈ 57019’
10 = рад; 10 ≈ 0,017 рад
3600 – 2π рад
10 – х рад
3600 – 2π рад
х 0 – 1 рад

Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный ей круг – тригонометрическим.
Приняв точку пересечения окружности с положительной частью оси Ох за начало отсчета;
Выбрав положительное направление – против часовой стрелки, отрицательное – по часовой стрелке;
Отложив от начала отсчета дугу в 1 рад, мы получим, что тригонометрическая окружность в некотором смысле «эквивалентна» понятию «числовая прямая».
x
y
0
1
1
0
«+»
«−»
1

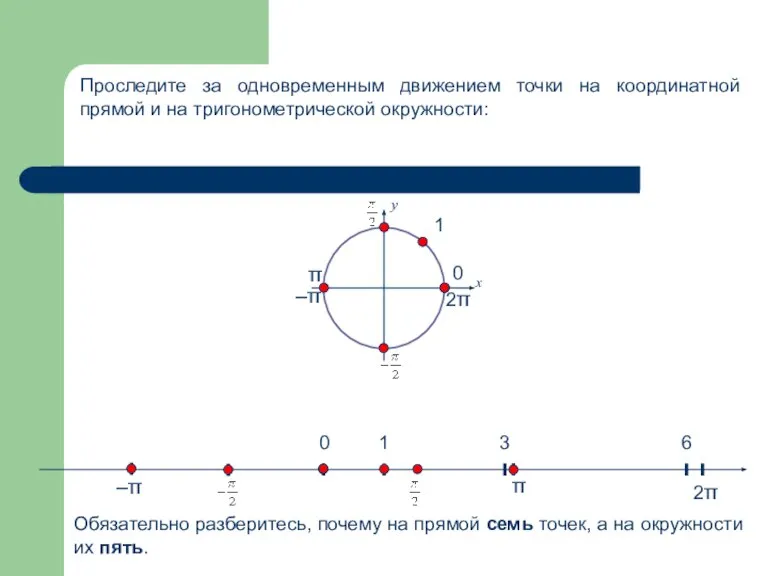
0
1
0
3
2π
6
π
π
2π
у
х
1
–π
–π
Проследите за одновременным движением точки на координатной прямой и на тригонометрической окружности:
Обязательно разберитесь, почему на прямой семь точек, а на окружности их пять.

Так как дуги – это части окружности, то длины некоторых из них будут выражены через число π (объясните почему).
Откладывая в положительном и отрицательном направлениях от начала отсчета прямой угол получим точки, соответствующие числам …
и (объясните
почему);
Выполнив поворот на развернутый угол в положительном и отрицательном направлениях получаем две совпадающие точки окружности с координатами…
и .
x
y
0
1
1
0
1

Напомним, что декартова система разбивается координатными осями на четыре координатные четверти – I, II, III и IV.
Задание 2. Определите границы координатных четвертей через углы поворота в радианной мере, взятых в положительном направлении.
Задание 3. Выполните предыдущее задание, при условии, что выбирается отрицательное направление углов поворота.
Задание 4. Какой координатной четверти принадлежит точка окружности с координатой 6,28?
x
y
0
1
1
0
1
I
II
III
IV

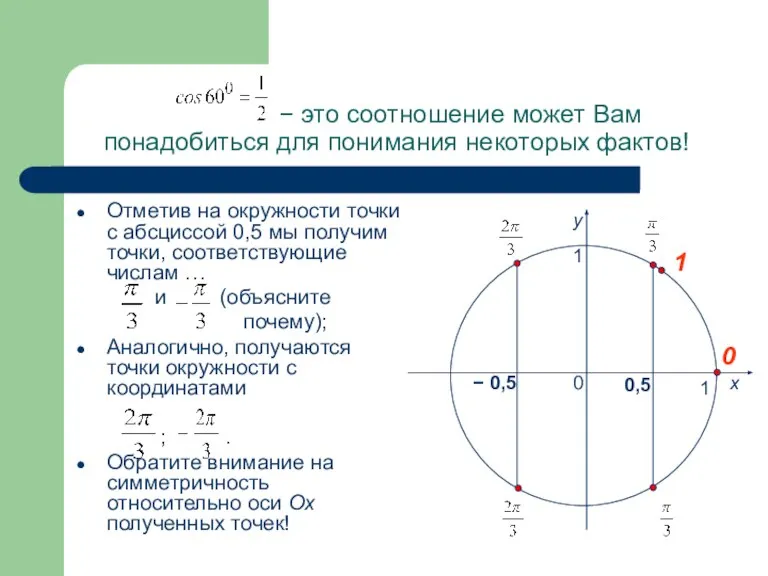
− это соотношение может Вам понадобиться для понимания некоторых фактов!
Отметив на окружности точки с абсциссой 0,5 мы получим точки, соответствующие числам …
и (объясните
почему);
Аналогично, получаются точки окружности с координатами
; .
Обратите внимание на симметричность относительно оси Ox полученных точек!
x
y
0
1
1
0
1
0,5
− 0,5

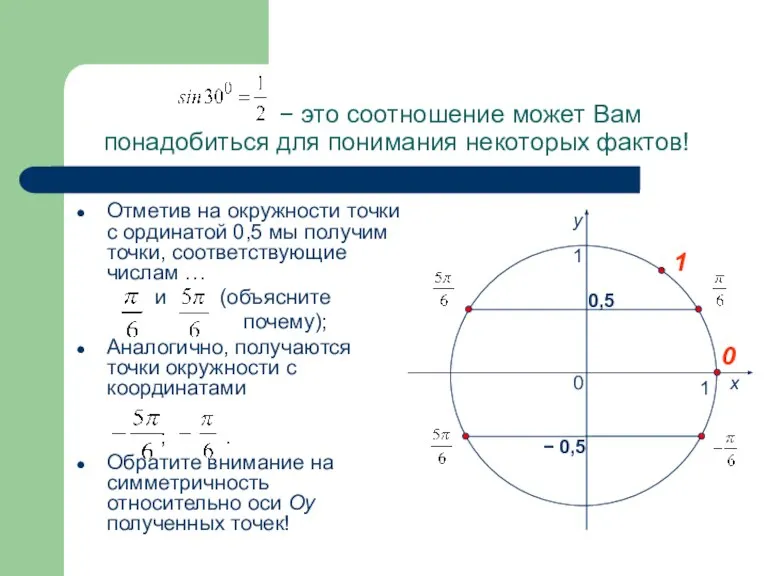
− это соотношение может Вам понадобиться для понимания некоторых фактов!
Отметив на окружности точки с ординатой 0,5 мы получим точки, соответствующие числам …
и (объясните
почему);
Аналогично, получаются точки окружности с координатами
; .
Обратите внимание на симметричность относительно оси Oy полученных точек!
x
y
0
1
1
0
1
0,5
− 0,5

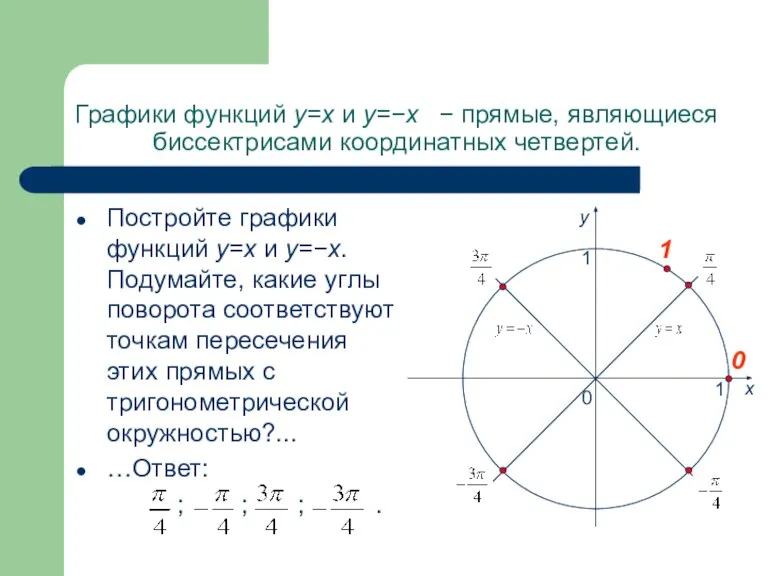
Графики функций y=x и y=−x − прямые, являющиеся биссектрисами координатных четвертей.
Постройте графики функций y=x и y=−x. Подумайте, какие углы поворота соответствуют точкам пересечения этих прямых с тригонометрической окружностью?...
…Ответ:
; ; ; .
x
y
0
1
1
0
1

Отметим на тригонометрической окружности точку А, соответствующую произвольному острому положительному углу поворота .
Если добавить полный поворот к углу α , то мы снова окажемся в той же точке А. Но теперь ее координата равна (подумайте)… .
Вообще, любую точку окружности можно получить поворотом на угол, вида α+2πn, где n∈Ζ и α∈[0;2π).
x
y
0
1
1
0
A(α)
A(α+2π)

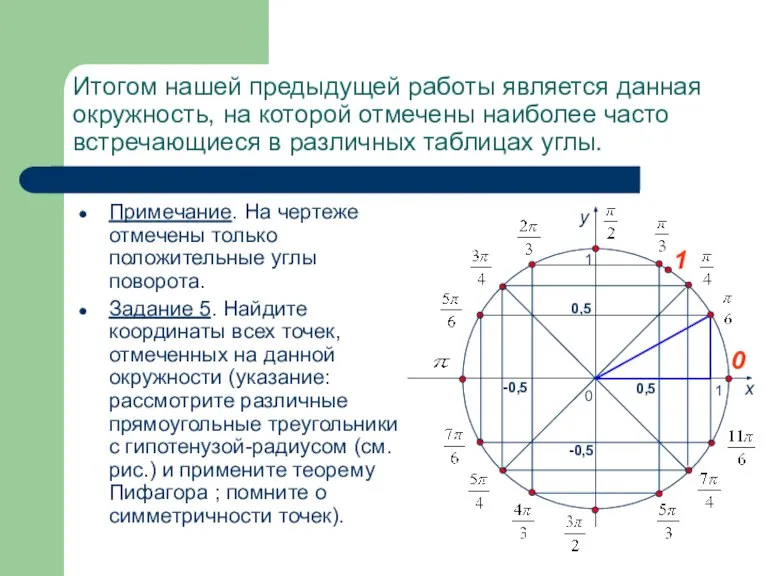
Итогом нашей предыдущей работы является данная окружность, на которой отмечены наиболее часто встречающиеся в различных таблицах углы.
Примечание. На чертеже отмечены только положительные углы поворота.
Задание 5. Найдите координаты всех точек, отмеченных на данной окружности (указание: рассмотрите различные прямоугольные треугольники с гипотенузой-радиусом (см.рис.) и примените теорему Пифагора ; помните о симметричности точек).
x
y
0
1
1
0
1
0,5
0,5
-0,5
-0,5

Ответы и решения.
Задание 2. - I четверть, - II четверть,
- III четверть, - IV четверть.
Задание 3. - I четверть, - II четверть,
- III четверть, - IV четверть

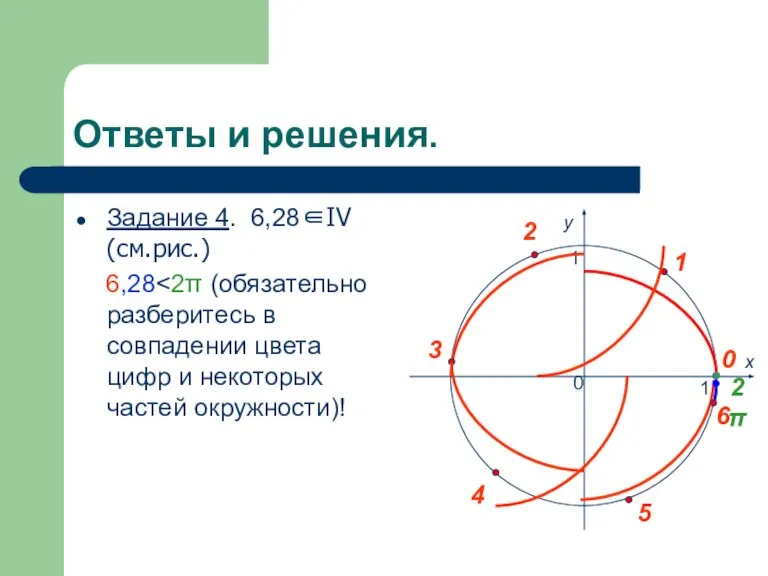
Ответы и решения.
Задание 4. 6,28∈IV (см.рис.)
6,28<2π (обязательно разберитесь в совпадении цвета цифр и некоторых частей окружности)!
x
y
0
1
1
0
1
2
3
4
5
6
2π