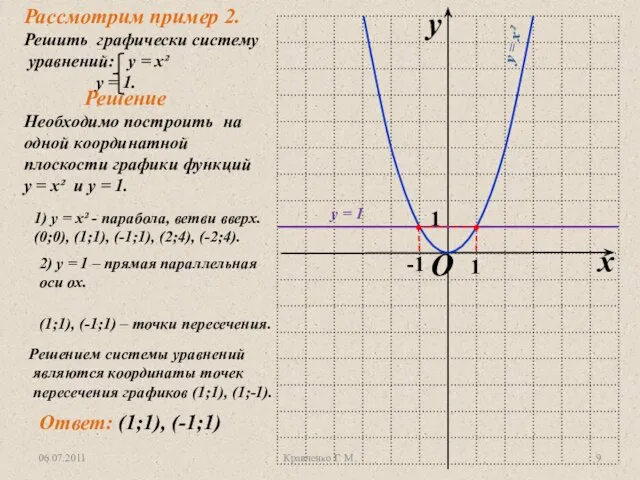
- 1;
у = - 2х², где k = - 2;
у = - 0,5х², где k = - 0,5;
k < 0
Графики у = f(x) и у = - f(x)
симметричны относительно
оси ох.
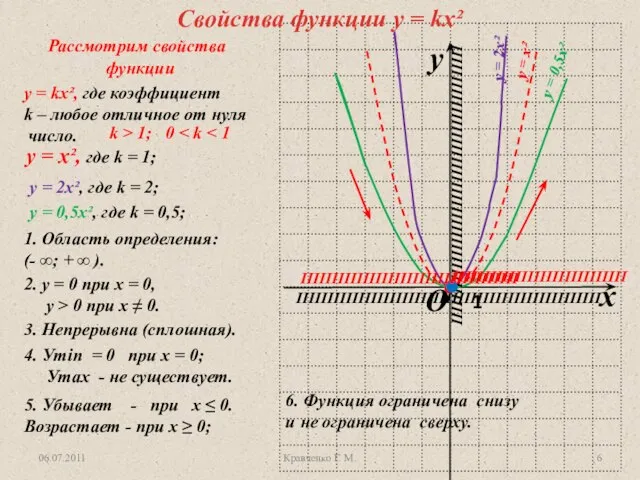
1. Область определения:
(- ∞; + ∞ ).
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
2. у = 0 при х = 0,
у < 0 при х ≠ 0.
.
3. Непрерывна (сплошная).
4. Уmax = 0 при х = 0;
Уmin - не существует.
5. Возрастает - при х ≤ 0.
убывает - при х ≥ 0;
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
6. Функция ограничена сверху
и не ограничена снизу
06.07.2011
Кравченко Г. М.


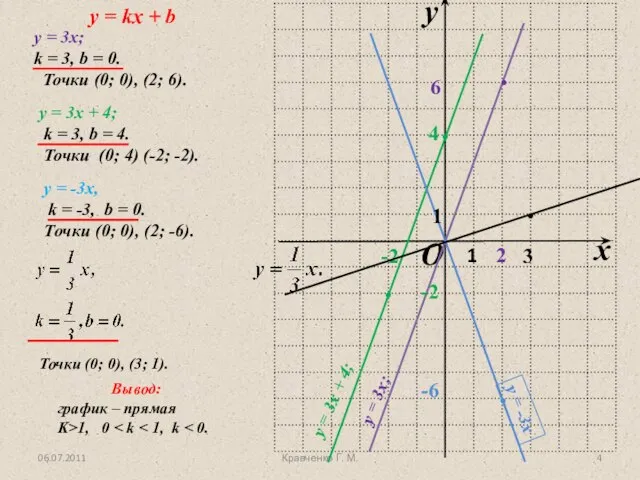
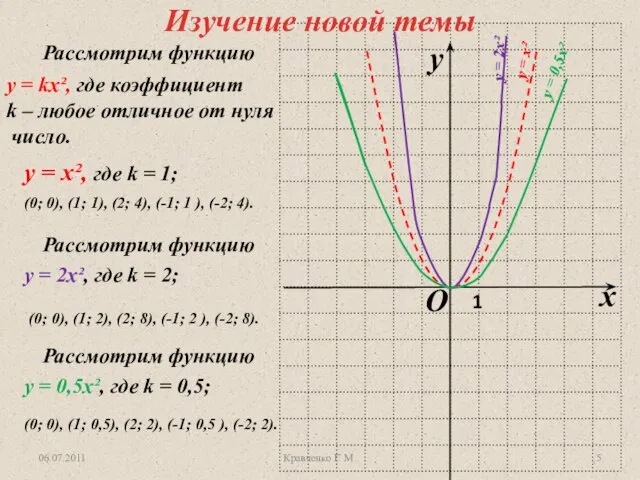

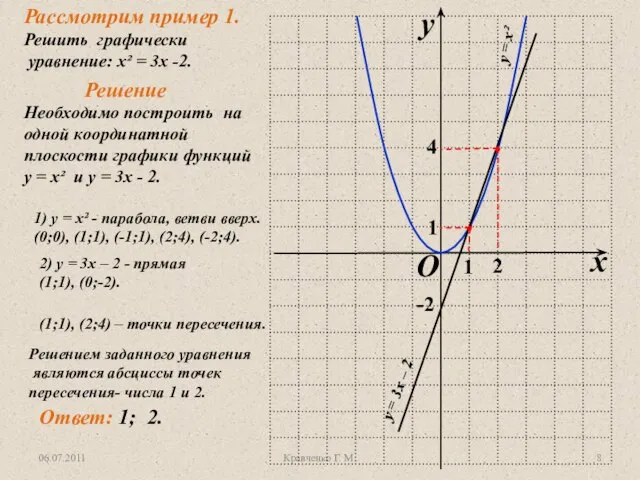
 Проценты. Задачи на концентрацию и сплавы
Проценты. Задачи на концентрацию и сплавы Размах и мода ряда чисел
Размах и мода ряда чисел Pervyy-urok-algebry.ppt
Pervyy-urok-algebry.ppt Презентация на тему Советы родителям будущих первоклассников
Презентация на тему Советы родителям будущих первоклассников  Свойства функции Алгебра 9 класс
Свойства функции Алгебра 9 класс  Презентация на тему Центральная Азия
Презентация на тему Центральная Азия  Муниципальное общеобразовательное учреждение «Лермонтовская средняя общеобразовательная школа»
Муниципальное общеобразовательное учреждение «Лермонтовская средняя общеобразовательная школа» Стандартный вид числа
Стандартный вид числа Решение задач с помощью систем уравнений 2 степени
Решение задач с помощью систем уравнений 2 степени Сложение чисел с разными знаками. 6 класс Новосёлова Е.А. МОУ «Усть-Мосихинская СОШ»
Сложение чисел с разными знаками. 6 класс Новосёлова Е.А. МОУ «Усть-Мосихинская СОШ» Музыкальные инструменты
Музыкальные инструменты Презентация на тему Дельфин Физминутка для глаз
Презентация на тему Дельфин Физминутка для глаз  Методика обучения решению линейных неравенств с одной переменной
Методика обучения решению линейных неравенств с одной переменной Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»
Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»  Свойства функций
Свойства функций Квадрат суммы. Квадрат разности 7 класс
Квадрат суммы. Квадрат разности 7 класс Путешествие в страну дробных чисел
Путешествие в страну дробных чисел Свойство периодичности - презентация по Алгебре_
Свойство периодичности - презентация по Алгебре_ Сложение и вычитание алгебраических дробей С разными знаменателями
Сложение и вычитание алгебраических дробей С разными знаменателями Функция y= ІхІ
Функция y= ІхІ Основные формулы тригонометрии 10 класс
Основные формулы тригонометрии 10 класс Доказательство тождеств
Доказательство тождеств Презентация на тему Зрительные Искажения
Презентация на тему Зрительные Искажения  Формула корней квадратного уравнения
Формула корней квадратного уравнения Элементы алгебры
Элементы алгебры Алгебраические комедии софизмы - презентация по Алгебре
Алгебраические комедии софизмы - презентация по Алгебре Бином Ньютона
Бином Ньютона Решение квадратных уравнений
Решение квадратных уравнений