Содержание
- 2. Определение: Функция F(х) называется первообразной функции f(х) на промежутке Х, если Теорема: Если функция f(х) непрерывна
- 3. Пример: Решение. Данная функция может быть записана в виде:
- 4. Замечание 2: Если функция f(х) определена на промежутке Х и в точке имеет разрыв в виде
- 5. Основные свойства неопределенного интеграла.
- 6. Основные методы Интегрирования.
- 7. Табличный. Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. Интегрирование с помощью замены переменной
- 8. Нахождение интеграла методом преобразования подынтегральной функции в сумму или разность.
- 9. Интегрирование методом замены переменной.
- 11. Интегрирование выражений, содержащих радикалы, методом подстановки.
- 13. Интегрирование алгебраических дробей.
- 14. Интегрирование по частям. Prezented.Ru
- 17. Скачать презентацию








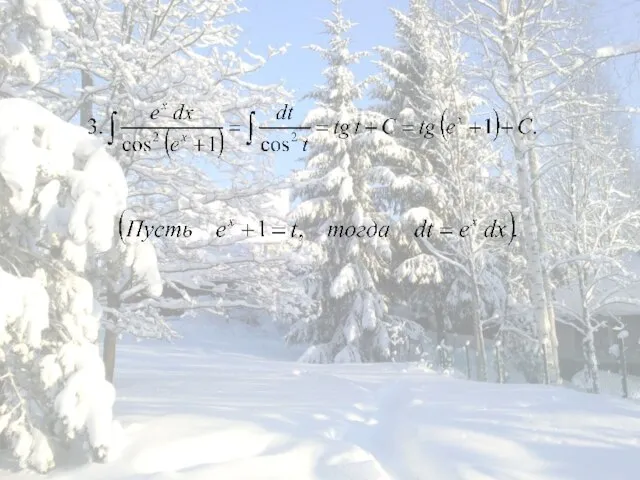





 Алгебраические дроби Основное свойство дроби Сокращение дробей
Алгебраические дроби Основное свойство дроби Сокращение дробей Алгебраические дроби Учитель математики МБОУ СОШ № 128 г.о.Самара Змеевская Светлана Николаевна
Алгебраические дроби Учитель математики МБОУ СОШ № 128 г.о.Самара Змеевская Светлана Николаевна  Урок по теме: “Тригонометрические формулы.” Ельцова Н.Г.,учитель МОУ «Гимназия №11», Г Норильск.
Урок по теме: “Тригонометрические формулы.” Ельцова Н.Г.,учитель МОУ «Гимназия №11», Г Норильск. Svoystva-funkcii-ysinx-i-ee-grafik.ppt
Svoystva-funkcii-ysinx-i-ee-grafik.ppt 7 класс. Учитель Козлова Нина Анатольевна, МОУ гимназия №6 г. Красноармейска
7 класс. Учитель Козлова Нина Анатольевна, МОУ гимназия №6 г. Красноармейска  Метод интервалов Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 учебный год
Метод интервалов Подготовила: учитель математики МОУ сош №30 имени А.И.Колдунова Кутоманова Е.М. 2010-2011 учебный год  Квадратные уравнения
Квадратные уравнения Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Что такое функция 7 класс
Что такое функция 7 класс Применение неравенств и их свойств
Применение неравенств и их свойств Экскурсия в историю математики
Экскурсия в историю математики Решение простейших логарифмических логарифмических уравнений
Решение простейших логарифмических логарифмических уравнений Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко
Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная шко Презентация на тему Виды и особенности экологических правоотношений
Презентация на тему Виды и особенности экологических правоотношений Презентация на тему Протекционизм
Презентация на тему Протекционизм  Абу Абдамах Ибн батутта
Абу Абдамах Ибн батутта  Функция y=sinx. Свойства. Преобразование графиков
Функция y=sinx. Свойства. Преобразование графиков Последовательности 2011 Васильева Е.Е.
Последовательности 2011 Васильева Е.Е. Решение неравенств второй степени с одной переменной 9 класс
Решение неравенств второй степени с одной переменной 9 класс Как построить график функции у = mf(x),если известен график функции у = f(x)
Как построить график функции у = mf(x),если известен график функции у = f(x) Статистические характеристики Среднее арифметическое ряда Размах ряда Мода ряда Медиана ряда
Статистические характеристики Среднее арифметическое ряда Размах ряда Мода ряда Медиана ряда  Решение уравнений и неравенств, содержащих модуль, методом интервалов
Решение уравнений и неравенств, содержащих модуль, методом интервалов Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»
Материал к внеклассным занятиям по математике в 9-11 классах « Алгебраические методы решения прикладных задач на экстремум»  Свойства и график функции СИНУС
Свойства и график функции СИНУС Презентация на тему Контрольная карта Шухарта
Презентация на тему Контрольная карта Шухарта  Умножение и деление степеней
Умножение и деление степеней Презентация на тему Особенности прохождения гос. службы в правоохранит. органах
Презентация на тему Особенности прохождения гос. службы в правоохранит. органах  Презентация на тему Научно-техническая революция XXв
Презентация на тему Научно-техническая революция XXв