Решение неравенств методом интервалов

0
x
y
Пусть графиком функции y=f(x) является некоторая гладкая кривая:
y=f(x)
Очевидно, что D(f)=E(f)=. Обратим свое внимание на значения аргумента x1 , x2 , x3 , x4 – в этих точках график функции пересекает ось Ох или касается её. Это – так называемые нули функции (ординаты этих точек равны 0, т.е. f(x1)= f(x2)= f(x3)= =f(x4) =0). Аналитически их можно найти, решая уравнение f(x)=0.
х4
х3
х2
х1

0
x
y
y=f(x)
Точки x1 , x2 , x3 , x4 разбивают область определения функции D(f) на промежутки знакопостоянства, т.е. промежутки, на которых функция имеет либо положительные значения (f(x)>0), либо отрицательные (f(x)<0). В нашем случае:
f(x)>0, при х∈(–; х1)(х2; х3) (х3; х4) и
х2
х1
х3
х4
f(x)<0, при х∈(х1; х2) (х4; +).

Опираясь на эту геометрическую иллюстрацию, мы можем вывести алгоритм решения неравенств, получивший название «метод интервалов».
Методом интервалов можно решить любое неравенство вида: f(x)0. При решении придерживаются следующей схемы (перепишите её в тетрадь!):
Найти D(f);
Найти нули функции, решая уравнение f(x)=0;
Отметить на D(f) все полученные нули;
Определить знак функции на каждом полученном промежутке;
Записать ответ, выбрав промежутки с соответствующим знаком.
Проиллюстрируем данную схему на нескольких примерах.
Пример 1. Решите неравенство .
Решение. Под функцией f(x) следует понимать выражение в левой части неравенства. Это дробно-рациональная функция.
1) D(f)=, кроме х= – 4; 2 (данные значения обращают знаменатель в нуль) .

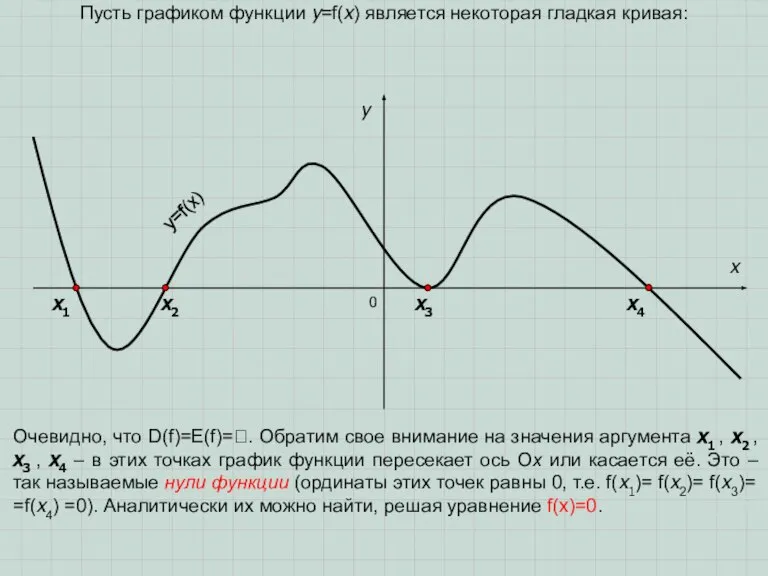
2) Найдем нули функции. Значение дроби равно нулю, если числитель этой дроби равен нулю, т.е. х= –1; 3; 7 – нули функции.
3) Обратите внимание, что точки разрыва функции (–4 и 2) всегда на числовой прямой будут пустыми (или «выколотыми»), а нули функции – в зависимости от знака неравенства (если знак неравенства строгий, то точки пустые, если нестрогий, то обычные).
–4
2
х
–1
3
7
+
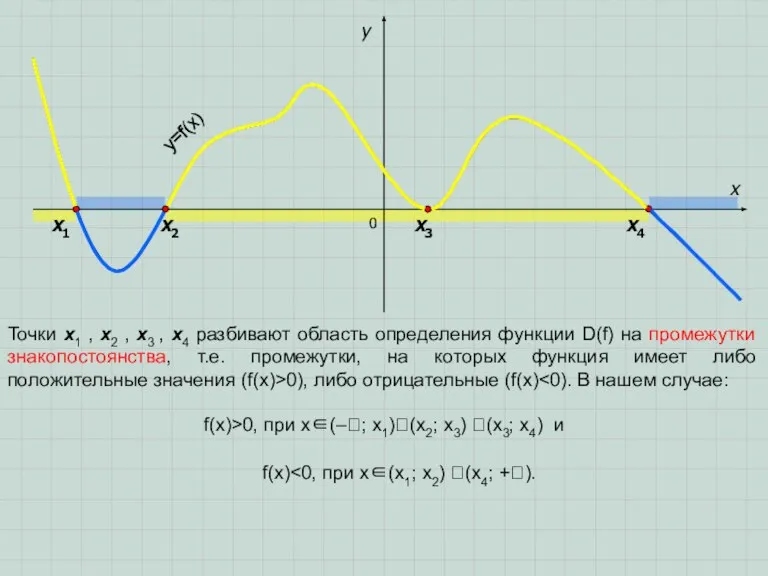
■ на остальных промежутках (двигаемся от крайнего справа промежутка влево) знаки расставляются по правилу: знак по сравнению с предыдущим меняется, если показатель степени линейного множителя нечетный и не изменяется, если показатель степени линейного множителя четный. В нашем случае получается… (см.рис.).
(х–3) (х–7) (х+1)
(х–2) (х+4)
2
3
4
–
–
+
–
–

Вышеизложенный метод определения знаков на интервалах по сути опирается на понятие «кратных» корней. Если Вам этот термин не знаком, то можно воспользоваться другим способом:
–4
2
х
–1
3
7
+
–
–
+
–
–
■ выбирая из каждого промежутка любое значение, подставляют в формулу, задающую данную функцию и определяют по полученной комбинации знак функции на каждом промежутке:
Как Вы можете убедиться – результат расстановки знаков такой же, как в предыдущем способе.

5) Остается записать ответ, выбрав промежутки соответствующие знаку неравенства. В нашем случае, знаку «≥» соответствуют промежутки со знаком «+». Важно не забыть х=3!!!
–4
2
х
–1
3
7
+
–
–
+
–
–
Ответ: х∈[–1; 2){3}[7; +).
Пример 2. Решите неравенство .
Решение. Перенесем все в левую часть неравенства: .
1) D(f)=, кроме х= – 1; 1, где f(x)= ;
2) Нулей функции нет, т.к. дискриминант квадратного трехчлена отрицательный;
3)
х
– 1
1
4) Проверьте себя, как Вы поняли правило расстановки знаков…
+
–
–