Слайд 2Важнейшая задача цивилизации -
Научить человека мыслить.
Т. Эдисон.

Слайд 3 Решить уравнение с параметром – это значит показать, каким образом для любого

значения параметра можно найти соответствующее множество корней уравнения, если корни существуют, или установить, что при этом значении параметра корней нет.
Слайд 4Решите квадратное уравнение
х2 -(2а+1)х+а2+а-2=0
Всегда ли это уравнение квадратное?
Да, это уравнение всегда

квадратное.
Слайд 5Найдите дискриминант уравнения.

Слайд 6Примените формулу корней квадратного уравнения.

Слайд 7Запишите ответ.
Ответ: х1=а+2; х2=а-1.

Слайд 8Решите уравнение: ах2+(1-а)х -1=0.
Всегда ли это уравнение квадратное?

Слайд 10Примените формулу корней квадратного уравнения.

Слайд 12Алгоритм решения «квадратного» уравнения с параметром
1.Найти значения параметра, при которых уравнение не

является квадратным (коэффициент при х2 равен нулю).
2.Решить уравнение при этих значениях параметра.
3.Найти дискриминант уравнения в остальных случаях.
4.Найти корни уравнения при всех значениях параметра.
Слайд 13Самостоятельная работа
Один из корней квадратного уравнения х2 +2ах+2-3а=0 равен 1. Найдите значение

параметра а и второй корень уравнения.
Слайд 15Вспомним алгоритм решения «квадратных» уравнений с параметром
1.Найти значения параметра, при которых уравнение

не является квадратным (коэффициент при х2 равен нулю).
2.Решить уравнение при этих значениях параметра.
3.Найти дискриминант уравнения в остальных случаях.
4.Найти корни уравнения при всех значениях параметра.














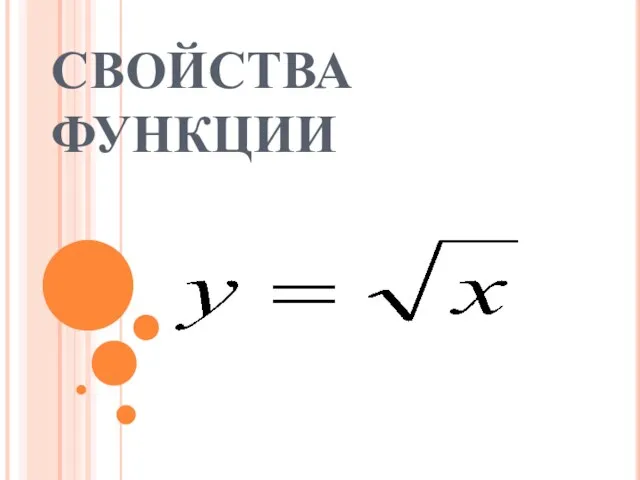 Свойства функции
Свойства функции Решение квадратных неравенств
Решение квадратных неравенств Рекурсия
Рекурсия Презентация на тему Контрольная карта Шухарта
Презентация на тему Контрольная карта Шухарта  Применение производной к исследованию функций
Применение производной к исследованию функций Приращение аргумента. Приращение функции
Приращение аргумента. Приращение функции Неравенства с двумя переменными
Неравенства с двумя переменными Функции и их графики 10 класс
Функции и их графики 10 класс Применение производной для исследования функций. 1. Нахождение промежутков возрастания функции. 2. Нахождение промежутков убыв
Применение производной для исследования функций. 1. Нахождение промежутков возрастания функции. 2. Нахождение промежутков убыв Подготовка к ГИА Алгебра 9 класс Учитель – Абрамова Т.А.
Подготовка к ГИА Алгебра 9 класс Учитель – Абрамова Т.А.  Статистическое определение вероятности
Статистическое определение вероятности Применение свойства непрерывности функции при решении неравенств методом интервалов
Применение свойства непрерывности функции при решении неравенств методом интервалов Pervyy-urok-algebry.ppt
Pervyy-urok-algebry.ppt Алгебра 8 класс Фадеева Светлана Виссарионовна МОУ Кожважская основная общеобразовательная школа
Алгебра 8 класс Фадеева Светлана Виссарионовна МОУ Кожважская основная общеобразовательная школа  Неравенства
Неравенства Презентация на тему Графики функций синуса и косинуса и их свойства
Презентация на тему Графики функций синуса и косинуса и их свойства Линейная функция
Линейная функция  Решение рациональных уравнений
Решение рациональных уравнений Степень с рациональным показателем Действия со степенями
Степень с рациональным показателем Действия со степенями  Касательная к графику функции
Касательная к графику функции Решение линеиных неравенств - презентация по Алгебре_
Решение линеиных неравенств - презентация по Алгебре_ Решение квадратных неравенств - презентация по Алгебре_
Решение квадратных неравенств - презентация по Алгебре_ Презентация на тему Использование нормирования
Презентация на тему Использование нормирования Презентация на тему Порядок возникновения изменения и прекращения права природопользования
Презентация на тему Порядок возникновения изменения и прекращения права природопользования  Элементы комбинаторики
Элементы комбинаторики Системы уравнений
Системы уравнений Тригонометрические уравнения
Тригонометрические уравнения Удивительные квадратные уравнения
Удивительные квадратные уравнения