Содержание
- 2. Многообразие видов уравнений и методов их решений во всех частях КИМ показательные; логарифмические; тригонометрические; иррациональные; уравнения,
- 3. Формулировки заданий укажите промежуток, которому принадлежит корень уравнения; найдите сумму ( произведение) корней уравнения; укажите количество
- 4. Неравенства в КИМах дробно-рациональные; логарифмические; показательные; степенные; иррациональные; комбинированные, содержащие функции разных видов.
- 5. Формулировки заданий решите неравенство; укажите множество решений неравенств; вычислите сумму всех натуральных решений неравенства; найдите наименьшее
- 6. 1 2 -1 0 1. Укажите промежуток, содержащий корни уравнения. 2. Найдите сумму корней уравнения 3.
- 7. Применение методов решения уравнений и неравенств
- 8. Способы решения систем уравнений подстановка сложение графически
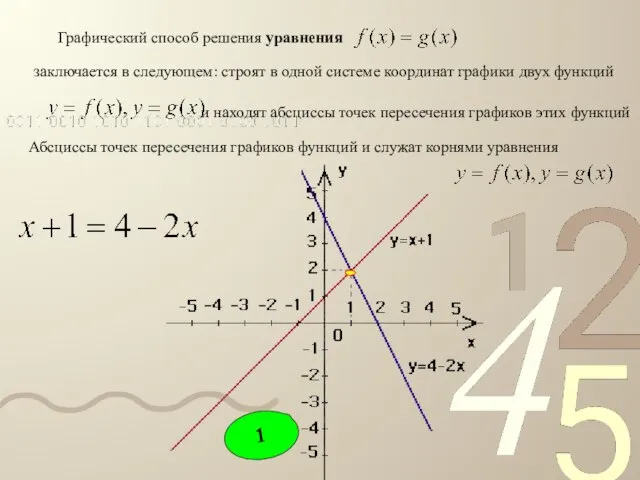
- 9. Абсциссы точек пересечения графиков функций и служат корнями уравнения Графический способ решения уравнения заключается в следующем:
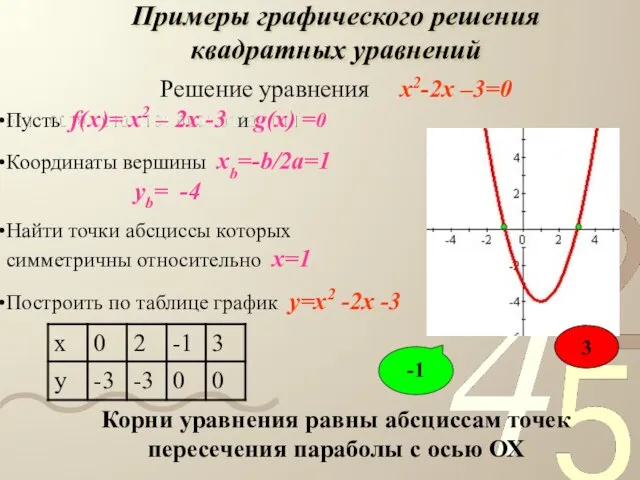
- 10. Пусть f(x)= x2 – 2x -3 и g(x) =0 Координаты вершины xb=-b/2a=1 yb= -4 Найти точки
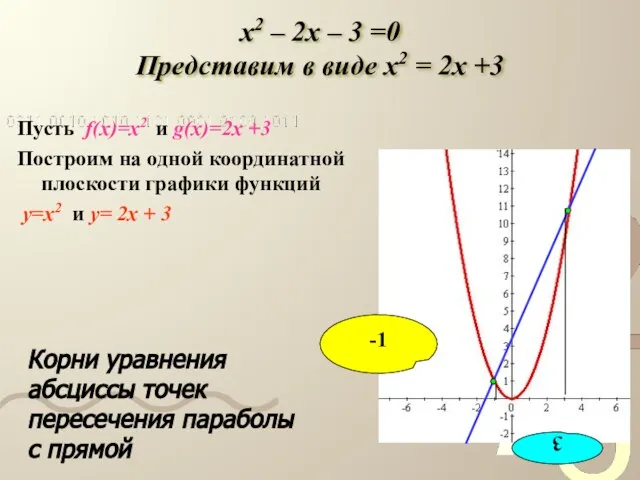
- 11. x2 – 2x – 3 =0 Представим в виде x2 = 2x +3 Пусть f(x)=x2 и
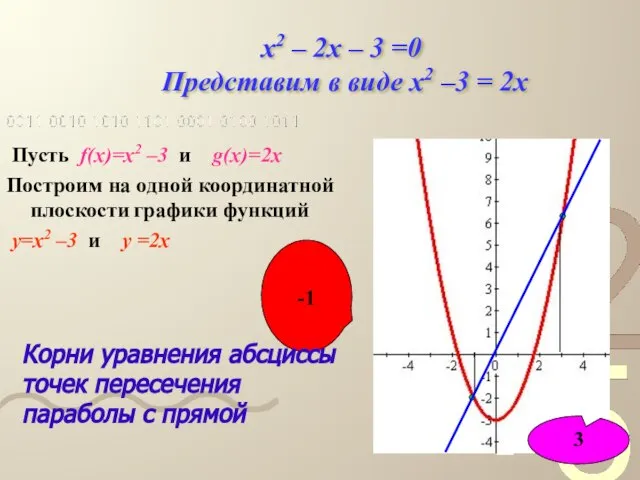
- 12. x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x Пусть f(x)=x2 –3
- 13. "Графический способ решения уравнений и неравенств"
- 14. Графический метод решения некоторых уравнений весьма эффективен, когда нужно установить, сколько корней имеет уравнение.
- 15. Графический метод при определении количества корней уравнения 1 2 3 4 5
- 16. На зарядку становись!
- 17. Неравенства Найти наименьшее натуральное решение неравенства Решить неравенства Найти область определения функции
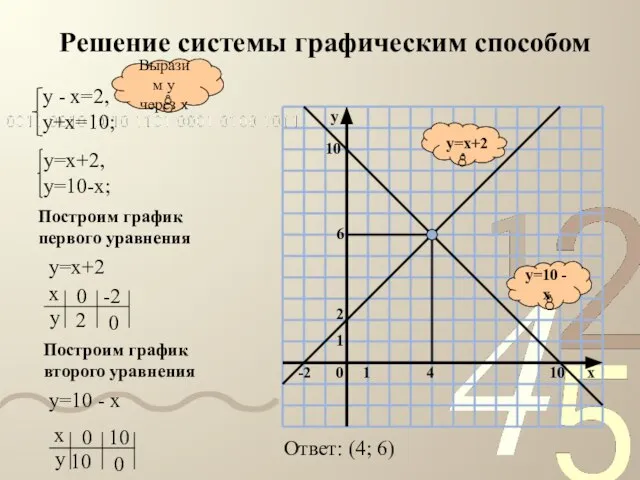
- 18. Решение системы графическим способом y=10 - x y=x+2 Выразим у через х Построим график первого уравнения
- 19. Решение систем уравнений Найти сумму х+у, где (х;у) – решение системы Найти произведение х*у, где (х;у)
- 20. ЕГЭ. Задания из части С. При каком значении р уравнение имеет три корня При каком значении
- 23. Скачать презентацию









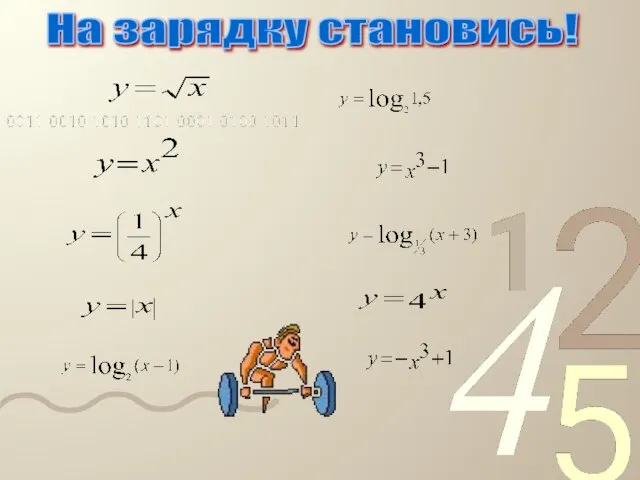




 Решение линеиных неравенств - презентация по Алгебре_
Решение линеиных неравенств - презентация по Алгебре_ Презентация на тему Методы Тагути
Презентация на тему Методы Тагути  Алгебраические дроби Основное свойство дроби Сокращение дробей
Алгебраические дроби Основное свойство дроби Сокращение дробей Презентация на тему Понятие и предмет международного частного права
Презентация на тему Понятие и предмет международного частного права  Презентация на тему Государственная служба и государственные служащие
Презентация на тему Государственная служба и государственные служащие  Всё о неравенствах Работу выполнил Попов Игорь ученик 9-класса
Всё о неравенствах Работу выполнил Попов Игорь ученик 9-класса Функции и их графики - презентация по Алгебре_
Функции и их графики - презентация по Алгебре_ Нестандартно мыслим
Нестандартно мыслим Формулы приведения
Формулы приведения Арифметическая прогрессия
Арифметическая прогрессия Issledovanie-funkciy-i-postroenie-grafikov.ppt
Issledovanie-funkciy-i-postroenie-grafikov.ppt Тізімдер мен кестелер
Тізімдер мен кестелер Умножение и деление степеней
Умножение и деление степеней Презентация на тему философия тождества
Презентация на тему философия тождества  Статистическое определение вероятности
Статистическое определение вероятности Логические законы и правила преобразования логических выражений
Логические законы и правила преобразования логических выражений Обратные тригонометрические функции
Обратные тригонометрические функции Многочлены
Многочлены Неопределенный интеграл
Неопределенный интеграл Алгебра модуля
Алгебра модуля Стандартный вид числа
Стандартный вид числа Арифметические действия над положительными и отрицательными числами
Арифметические действия над положительными и отрицательными числами Презентация на тему Аварии на радиационно-опасных объектах
Презентация на тему Аварии на радиационно-опасных объектах  Виды алгоритмов
Виды алгоритмов Первообразная Правила нахождения первообразных
Первообразная Правила нахождения первообразных  Презентация на тему Основные положения модели управления качеством А. Фейгенбаума
Презентация на тему Основные положения модели управления качеством А. Фейгенбаума  Сложение и вычитание чисел с разными знаками
Сложение и вычитание чисел с разными знаками Производная степенной функции. Ее геометрический смысл
Производная степенной функции. Ее геометрический смысл