Содержание
- 2. О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой башне, в малой
- 3. Симметрия (греч.) - соразмерность, пропорциональность, одинаковость в расположении частей.
- 4. Виды симметрии Симметрия относительно прямой Симметрия относительно точки Поворот Симметрия в природе Симметрия в архитектуре
- 5. Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину
- 9. Являются ли данные точки симметричными ? М М1 m С D b B В1 а Рисунок
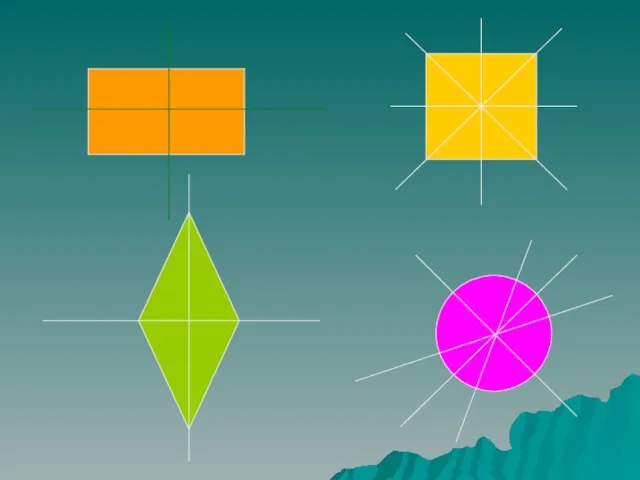
- 10. А Сколько осей симметрии имеет: Отрезок Прямая Луч А В а О Е одна множество Ни
- 11. Какие из этих фигур имеют ось симметрии? Сколько осей симметрии имеет каждая фигура? 5 6 3
- 12. Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1
- 14. О
- 15. О
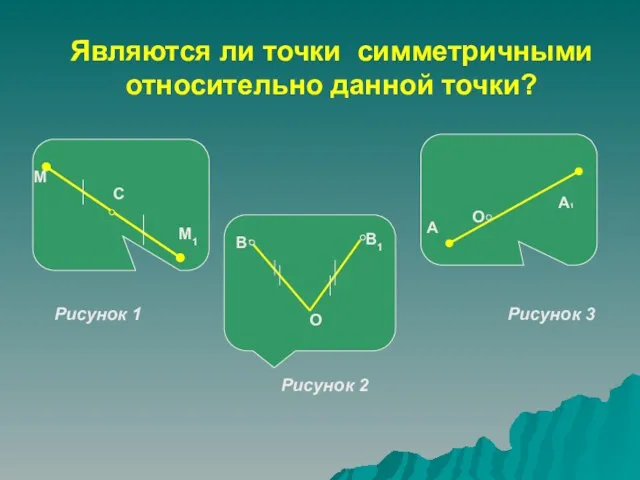
- 17. Являются ли точки симметричными относительно данной точки? Рисунок 1 Рисунок 2 Рисунок 3 М1 В В1
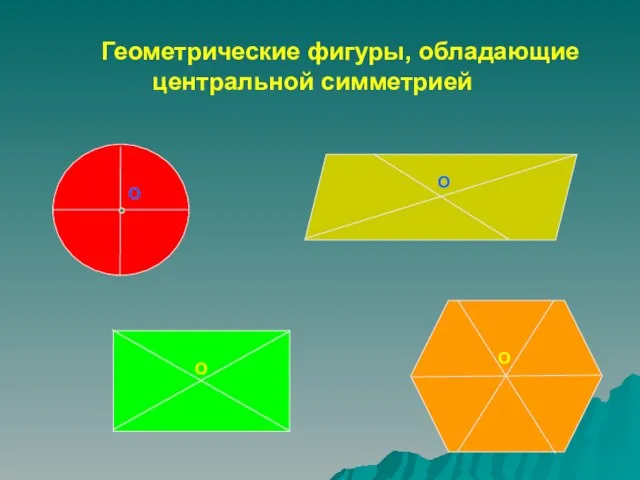
- 18. О О О О Геометрические фигуры, обладающие центральной симметрией
- 19. Имеют ли центр симметрии: Отрезок Прямая Луч Задачи О один множество Ни одного О О1 О2
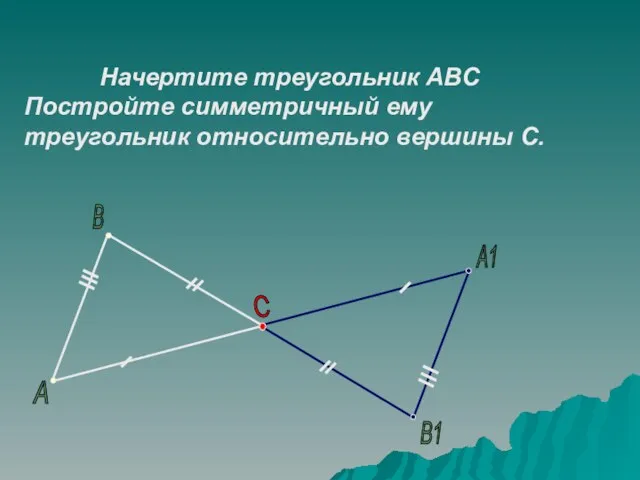
- 20. А В С А1 В1 Начертите треугольник АВС Постройте симметричный ему треугольник относительно вершины С.
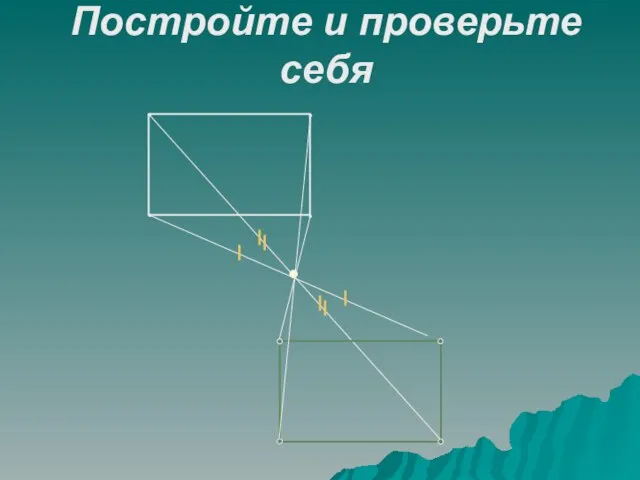
- 21. Постройте и проверьте себя
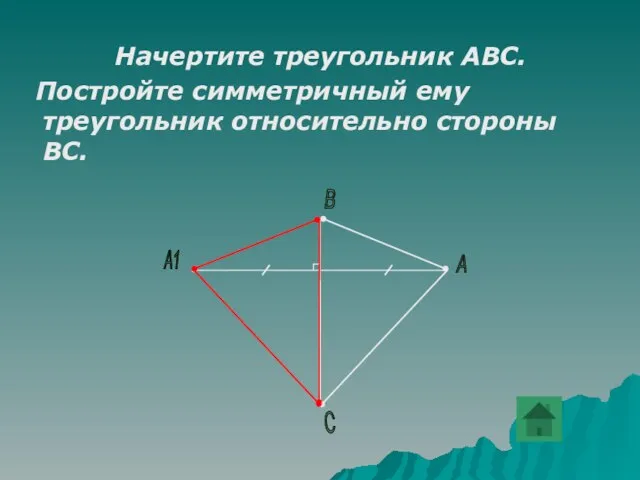
- 22. Начертите треугольник АВС. Постройте симметричный ему треугольник относительно стороны ВС. А В А1 С
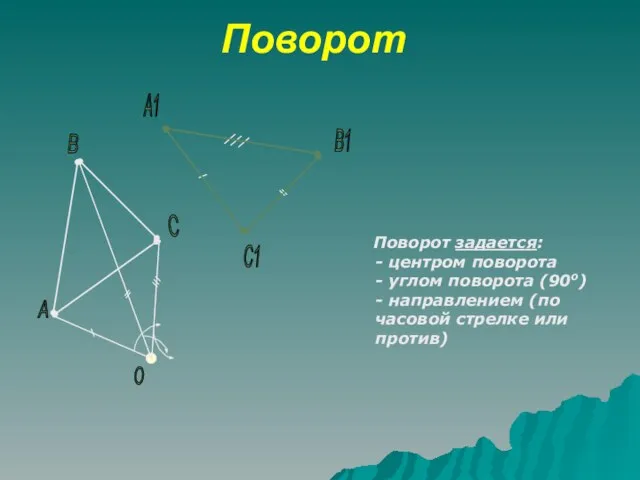
- 23. Поворот Поворот задается: - центром поворота - углом поворота (90о) - направлением (по часовой стрелке или
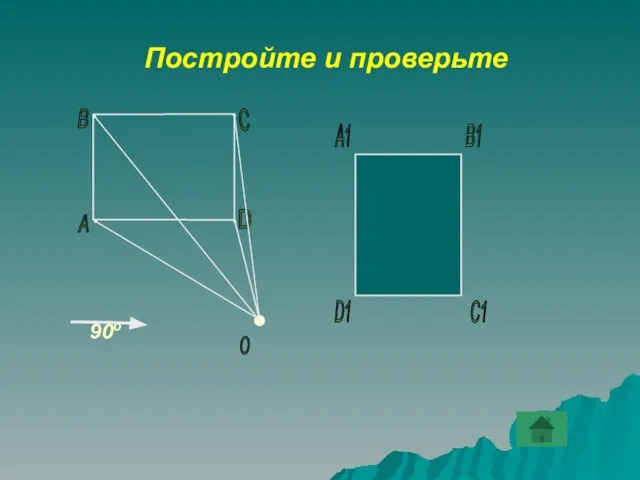
- 24. В1 С1 D1 А1 D Постройте и проверьте А В С О 90о
- 25. Симметрия в природе
- 28. Симметрия в балете Знаменитые фуэте, когда балерина вращается на одной ножке 6 раз, 12, …, 32
- 29. Винтовая симметрия Листья располагаются на стволе по винтовой линии, чтобы заслонять друг от друга солнечный свет.
- 30. Казанский собор Симметрия и антисимметрия в архитектуре
- 32. Антисимметрия – это противоположность симметрии, ее отсутствие.
- 33. Диссимметрия – это частичное отсутствие симметрии, её расстройство, выраженное в наличии одних симметричных свойств и отсутствии
- 36. С какими новыми понятиями познакомились? Что нового узнали о геометрических фигурах? Приведите примеры геометрических фигур, обладающих
- 38. Скачать презентацию


























 ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Деление окружности Векторы на плоскости и в пространстве, векторный метод решения задач
Векторы на плоскости и в пространстве, векторный метод решения задач Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии
Геометрия - наука, изучающая формы, размеры и взаимное расположение фигур - презентация по Геометрии Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием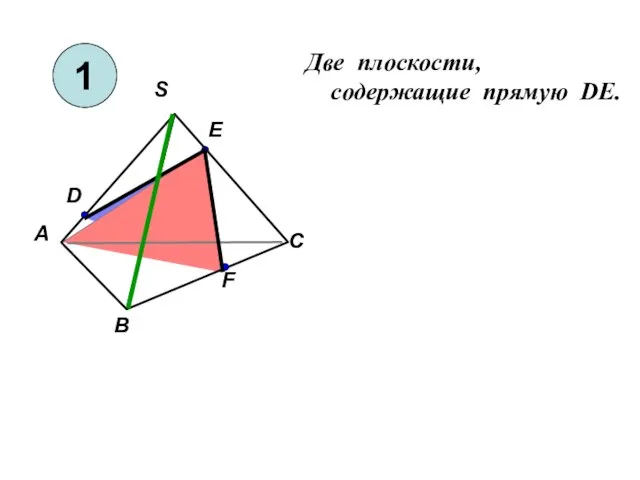 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Что такое геометрия
Что такое геометрия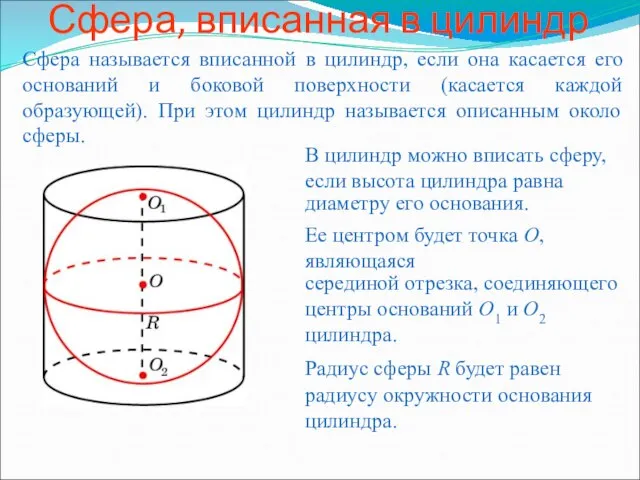 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Многоугольники
Многоугольники Построение графиков гармонических колебаний.
Построение графиков гармонических колебаний. Скалярное произведение в координатах
Скалярное произведение в координатах Теорема о сумме углов треугольника
Теорема о сумме углов треугольника Четырехугольники 9 класс
Четырехугольники 9 класс Признаки равенства треугольников. Устные задачи
Признаки равенства треугольников. Устные задачи Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Орнамент - математическое воплощение красоты
Орнамент - математическое воплощение красоты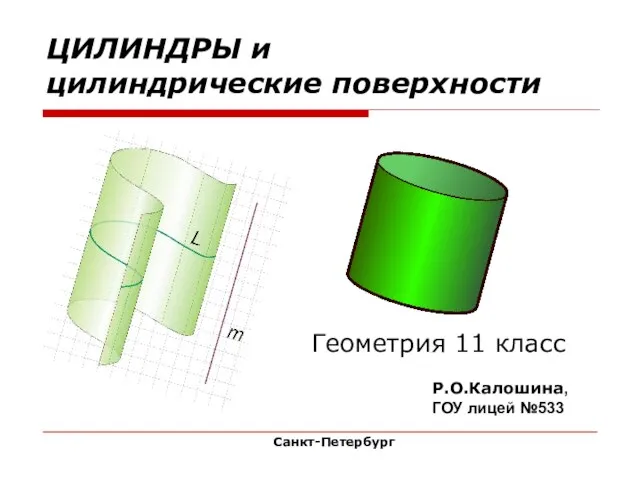 ЦИЛИНДРЫ и цилиндрические поверхности
ЦИЛИНДРЫ и цилиндрические поверхности Признаки паралельности прямых
Признаки паралельности прямых Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Удивительный квадрат (10 класс)
Удивительный квадрат (10 класс) Геометрия в архитектуре
Геометрия в архитектуре Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Свойства производной. Построение графиков функций. (Повторение материала 10 класса).
Свойства производной. Построение графиков функций. (Повторение материала 10 класса). Симметрия
Симметрия Графы
Графы Секреты квадрата и кубика
Секреты квадрата и кубика