Геометрия 10 класс - презентация по Геометрии

Содержание
Стереометрия
Аксиомы 1 Аксиомы 1,2 Аксиомы 1,2,3
Следствия 1,2,3
Задача

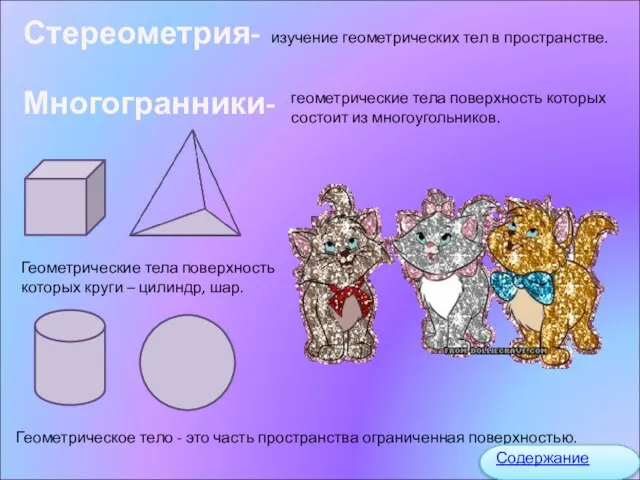
Стереометрия-
изучение геометрических тел в пространстве.
Многогранники-
геометрические тела поверхность которых состоит из многоугольников.
Геометрические тела поверхность которых круги – цилиндр, шар.
Геометрическое тело - это часть пространства ограниченная поверхностью.

Аксиомы

Через любые три точки, не лежащие на одной прямой, можно провести плоскость и при том только одну.

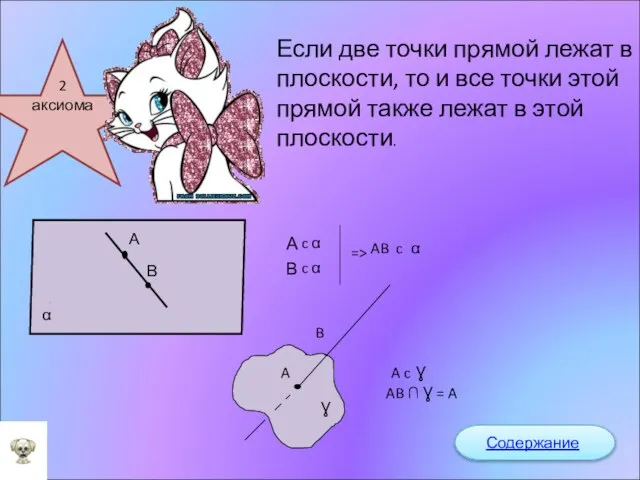
Если две точки прямой лежат в плоскости, то и все точки этой прямой также лежат в этой плоскости.

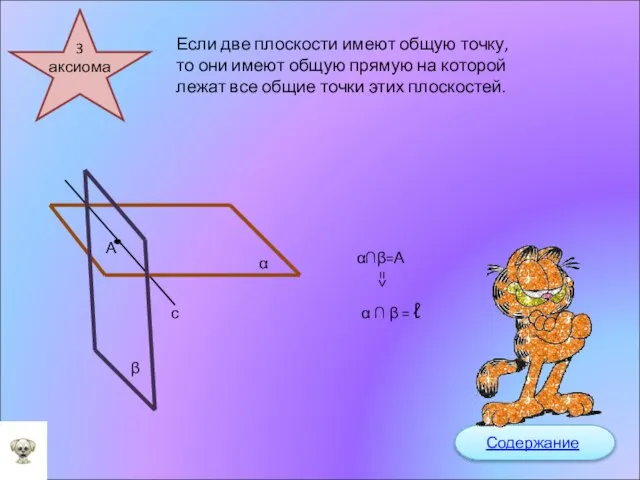
Если две плоскости имеют общую точку, то они имеют общую прямую на которой лежат все общие точки этих плоскостей.

Следствия

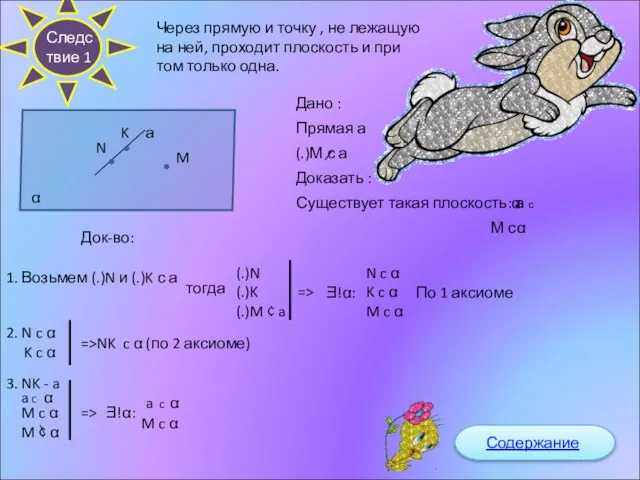
Через прямую и точку , не лежащую на ней, проходит плоскость и при том только одна.
α
α
α

Следствие 2
Через две пересекающие прямые можно провести плоскость и притом только одну.
β
а
M
N
b
Док-во:

Через две параллельные прямые можно провести плоскость и притом только одну.
Дано:
a//b
Доказать:
Ǝ!α: a c α
b c α
Доказательство:
α
M
a
b

Задача №16
Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости α. Лежат ли две другие вершины параллелограмма в плоскости α.
Дано:
ABCD- параллелограмм
BD∩AC=O
A c α ; B c α ; O c α
Доказать:
С с α
D c α
3. В с α
О с α

1. Сколько плоскостей можно провести через 3 точки?
Бесконечное кол-воБесконечное кол-во 2) 1
3) 43) 4 4) 2
2. Если две точки лежат в плоскости, то остальные точки лежат:
В другой плоскости В другой плоскости 2) в этой плоскости
3) На прямой
3. Если 2 плоскости имеют общую точку, то …..
4. Что проходит через прямую и точку не лежащую на ней:
ПлоскостьПлоскость 2) Прямая
5. Через 2 пересекающие прямые…..
6. Через 2 параллельные прямые можно…

ПРАВИЛЬНО