Содержание
- 2. Что общего у фигур, изображённых на экране?
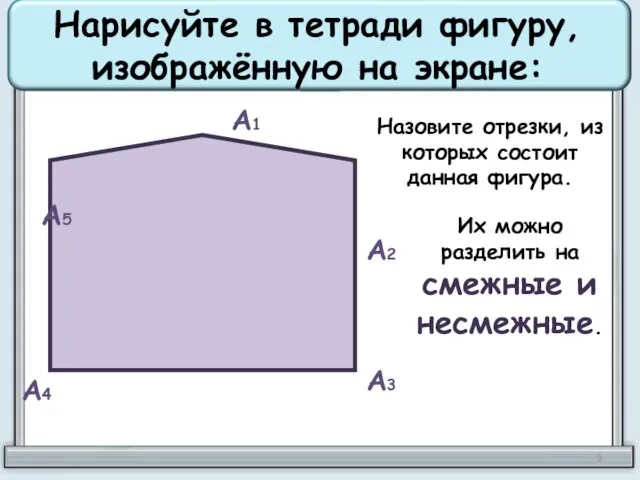
- 3. Нарисуйте в тетради фигуру, изображённую на экране: А1 А2 А3 А4 А5 Назовите отрезки, из которых
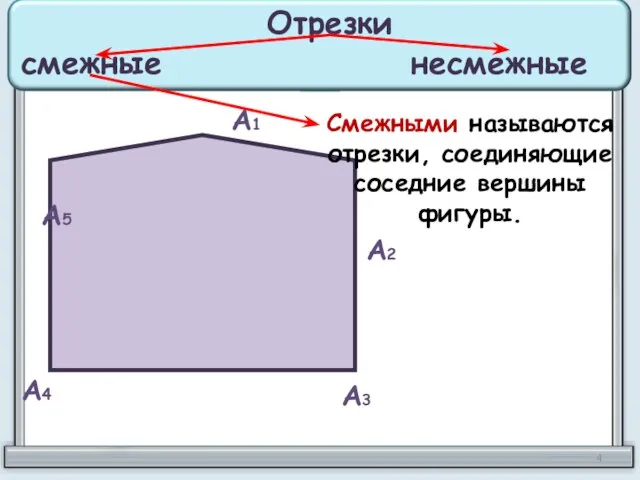
- 4. А1 А2 А3 А4 А5 Смежными называются отрезки, соединяющие соседние вершины фигуры. Отрезки смежные несмежные
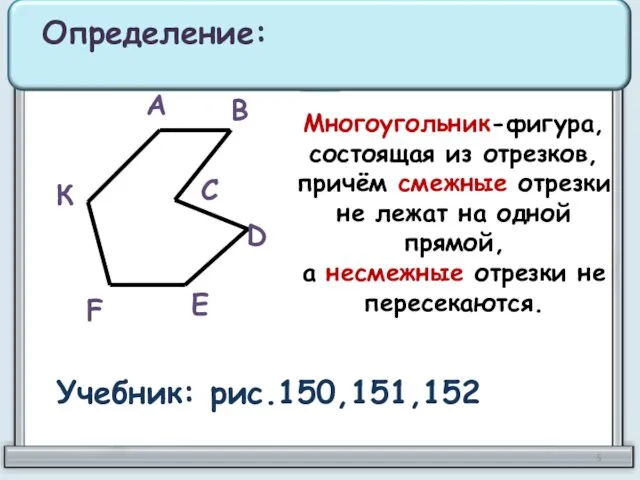
- 5. Многоугольник-фигура, состоящая из отрезков, причём смежные отрезки не лежат на одной прямой, а несмежные отрезки не
- 6. А1 А2 А3 А4 А5 Многоугольник А1А2А3А4А5 А1А2, А2А3, А3А4, А4А5, А5А1 - стороны Р- сумма
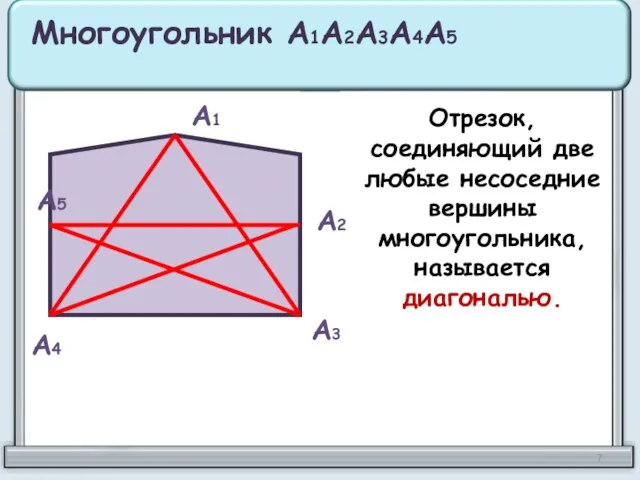
- 7. А1 А2 А3 А4 А5 Многоугольник А1А2А3А4А5 Отрезок, соединяющий две любые несоседние вершины многоугольника, называется диагональю.
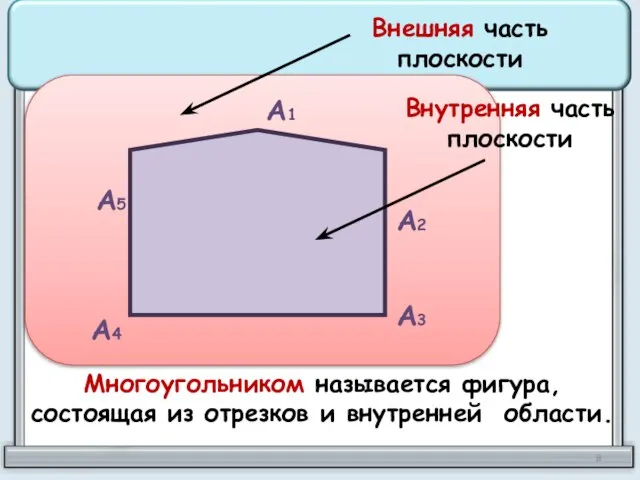
- 8. А1 А2 А3 А4 А5 Внешняя часть плоскости Внутренняя часть плоскости Многоугольником называется фигура, состоящая из
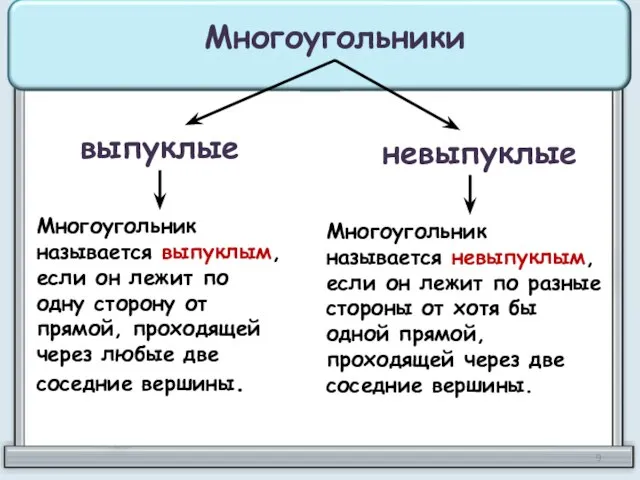
- 9. Многоугольники выпуклые невыпуклые Многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через
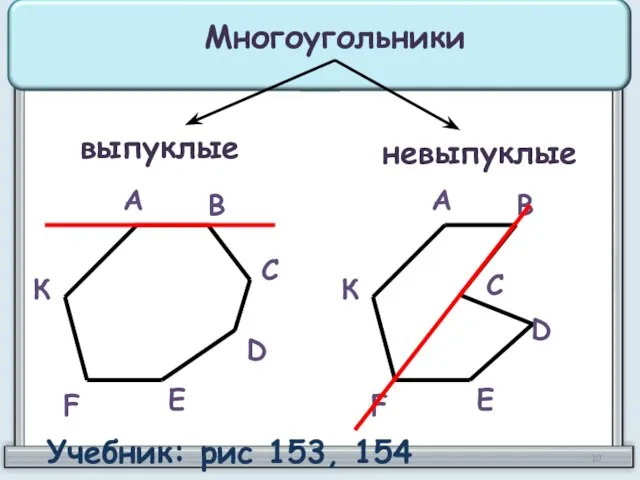
- 10. Многоугольники выпуклые невыпуклые А В С D Е F К А В С D Е F
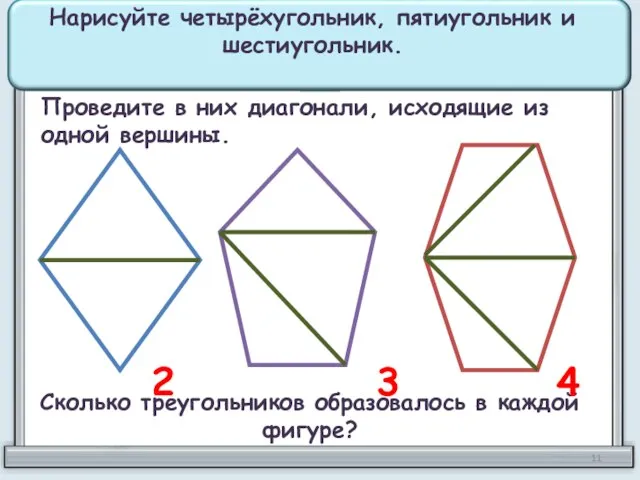
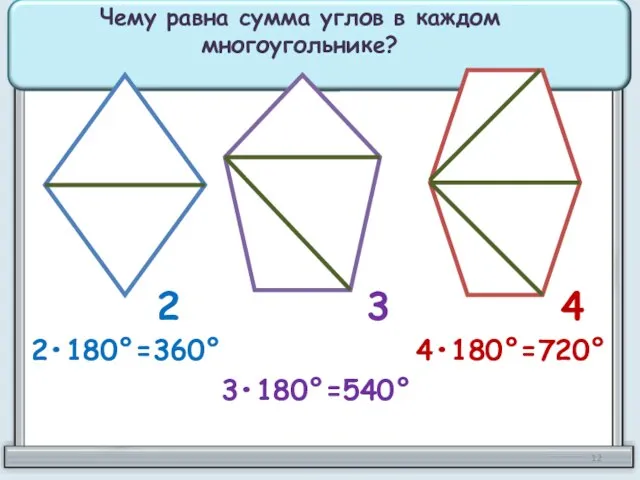
- 11. Нарисуйте четырёхугольник, пятиугольник и шестиугольник. Проведите в них диагонали, исходящие из одной вершины. Сколько треугольников образовалось
- 12. 2 3 4 Чему равна сумма углов в каждом многоугольнике? 2•180°=360° 3•180°=540° 4•180°=720°
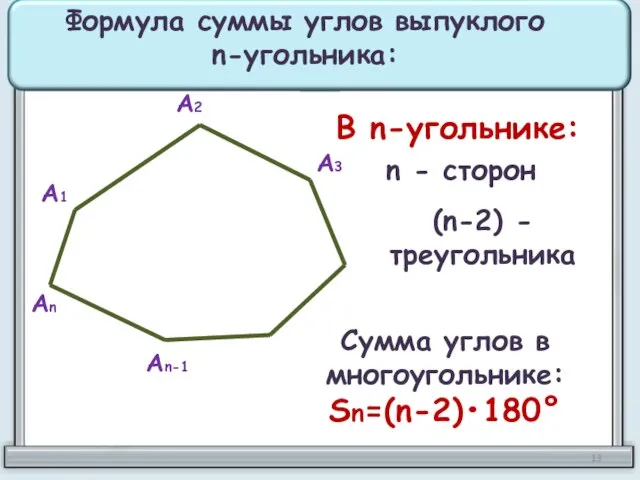
- 13. А1 А2 А3 Аn-1 Аn Формула суммы углов выпуклого n-угольника: В n-угольнике: n - сторон (n-2)
- 14. Выполните самостоятельно №364 из учебника S5=(5-2)•180°=3 •180°= 540° S6=(6-2)•180°=4 •180°= 720° S10=(10-2)•180°=8 •180°= 1440°
- 16. Скачать презентацию



 Объём призмы
Объём призмы Нахождение угла между скрещивающимися прямыми
Нахождение угла между скрещивающимися прямыми Объем конуса
Объем конуса Решение задач на вычисление площадей фигур
Решение задач на вычисление площадей фигур Объём пирамиды
Объём пирамиды Шар. Сфера
Шар. Сфера Понятие движения
Понятие движения Первый признак равенства треугольников
Первый признак равенства треугольников Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А.
Вписанная и описанная окружность. Работа по готовым чертежам. Урок №10. 8 класс. Учитель школы №327 Маркова Н.А. Вводное повторение курса геометрии
Вводное повторение курса геометрии Площади и объемы
Площади и объемы Прямоугольные треугольники 7 класс
Прямоугольные треугольники 7 класс Координатный метод
Координатный метод Геометрия Лобачевского
Геометрия Лобачевского Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах Двугранные углы - презентация по Геометрии_
Двугранные углы - презентация по Геометрии_ Геометрия. Как она возникла?
Геометрия. Как она возникла? Решение задач. Теорема о трех перпендикулярах.
Решение задач. Теорема о трех перпендикулярах. Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн
Решение задач на применение первого признака равенства треугольников МОУ ООШ Д. Старое Мелково Учитель: Костик Инна Станиславовн Двугранные углы
Двугранные углы Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Площади фигур. Зачёт
Площади фигур. Зачёт Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ Окружности
Окружности Трехгранный угол
Трехгранный угол Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Геометрические построения на плоскости
Геометрические построения на плоскости