Содержание
- 2. Определение производной: Найти производную функции по определению: © Комаров Р.А.
- 3. Вставьте вместо * Определение первообразной: © Комаров Р.А.
- 4. Будут ли первообразными следующие функции для функции © Комаров Р.А.
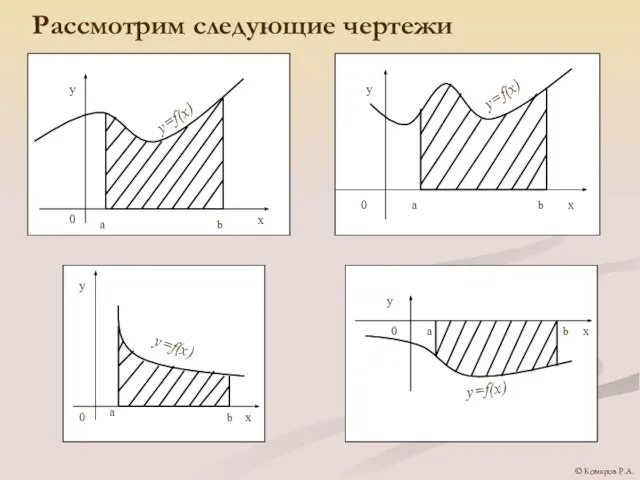
- 5. Рассмотрим следующие чертежи © Комаров Р.А.
- 6. Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми
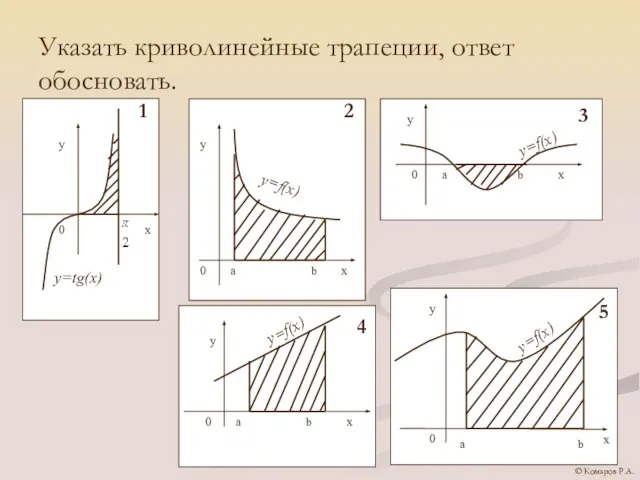
- 7. Указать криволинейные трапеции, ответ обосновать. © Комаров Р.А.
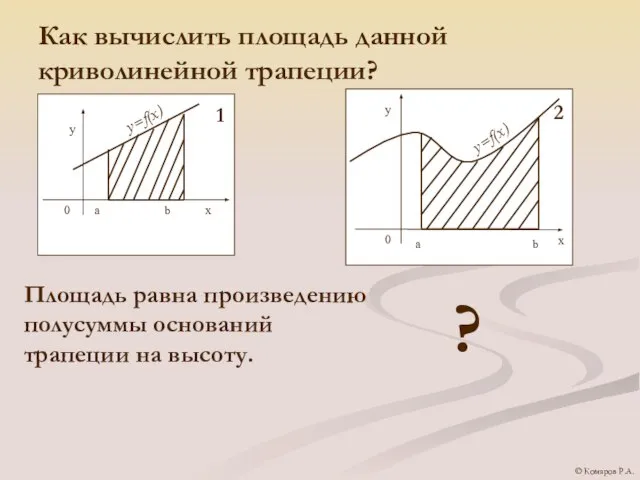
- 8. Как вычислить площадь данной криволинейной трапеции? Площадь равна произведению полусуммы оснований трапеции на высоту. ? ©
- 9. Площадь криволинейной трапеции © Комаров Р.А.
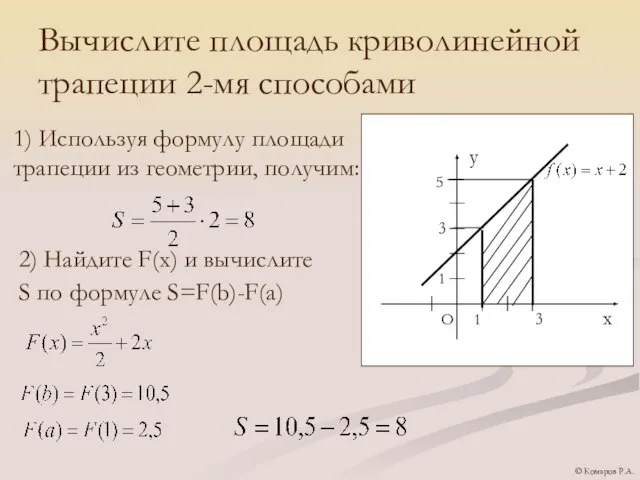
- 10. Вычислите площадь криволинейной трапеции 2-мя способами 1) Используя формулу площади трапеции из геометрии, получим: 2) Найдите
- 11. Теорема: Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее
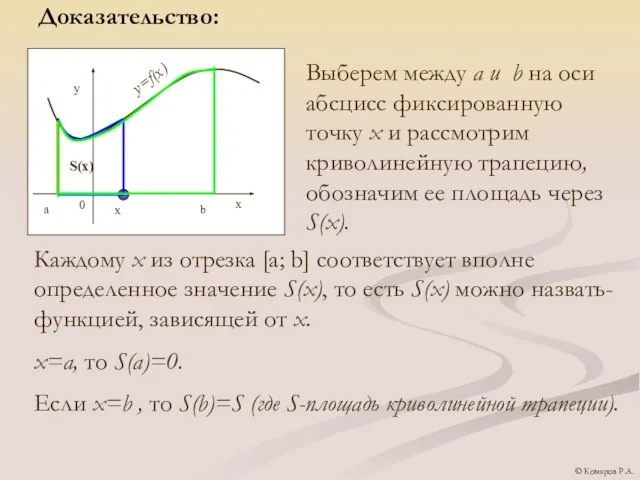
- 12. Доказательство: Выберем между a и b на оси абсцисс фиксированную точку х и рассмотрим криволинейную трапецию,
- 13. Докажем , что – это площадь криволинейной трапеции, опирающейся на отрезок[x; x+∆x] (площадь фигуры заштрихованной на
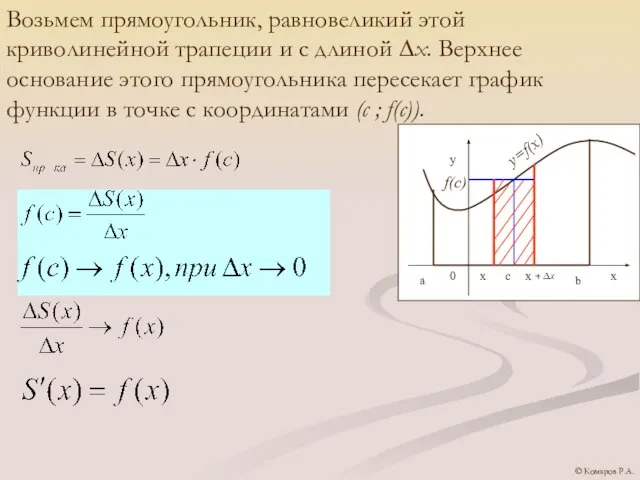
- 14. Возьмем прямоугольник, равновеликий этой криволинейной трапеции и с длиной ∆х. Верхнее основание этого прямоугольника пересекает график
- 15. Найдем С: Тогда Таким образом, мы доказали теорему и в дальнейшем площадь криволинейной трапеции будем вычислять
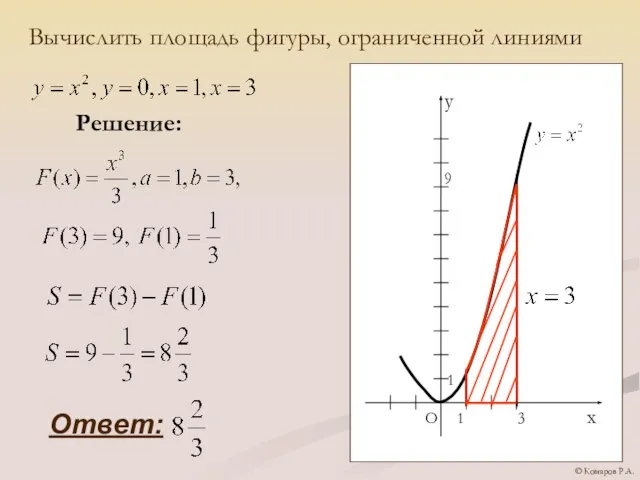
- 16. Вычислить площадь фигуры, ограниченной линиями Решение: Ответ: © Комаров Р.А.
- 18. Скачать презентацию





![Теорема: Если f – непрерывная и неотрицательная на отрезке [a; b] функция,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/310796/slide-10.jpg)
![Докажем , что – это площадь криволинейной трапеции, опирающейся на отрезок[x; x+∆x]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/310796/slide-12.jpg)

 Площади фигур на клетке
Площади фигур на клетке Тетраэдр
Тетраэдр Формула Гириха
Формула Гириха Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________
Преобразование графиков функций - презентация по Геометрии__________________________________________________________________________________________________________________ Многоугольники
Многоугольники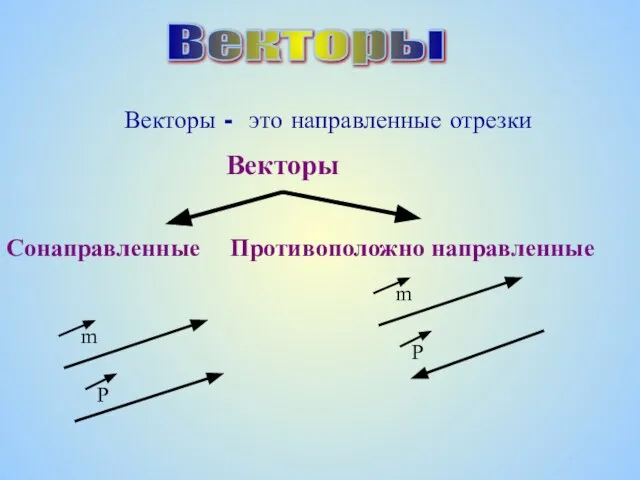 Векторы: Знакомство
Векторы: Знакомство Площади многоугольников
Площади многоугольников Измерение углов
Измерение углов Начертательная геометрия
Начертательная геометрия Что изучает геометрия 7 класс
Что изучает геометрия 7 класс Симметрия
Симметрия УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА" Окружность и круг
Окружность и круг Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Геометрические задачи на экстремум
Геометрические задачи на экстремум Подготовлю справочник по геометрии (или как повторить геометрию к экзамену)
Подготовлю справочник по геометрии (или как повторить геометрию к экзамену) Площадь многоугольника 8 класс
Площадь многоугольника 8 класс В мире треугольников
В мире треугольников Планиметрия
Планиметрия Измерение длин отрезков
Измерение длин отрезков Вводное повторение курса геометрии
Вводное повторение курса геометрии Правильная пирамида
Правильная пирамида Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Площади плоских геометрических фигур
Площади плоских геометрических фигур Доклад о «Сфере и шаре»
Доклад о «Сфере и шаре» Сечения многогранников плоскостью
Сечения многогранников плоскостью Теорема синусов и косинусов в задачах с практическим содержанием
Теорема синусов и косинусов в задачах с практическим содержанием Симметрия правит миром
Симметрия правит миром