Содержание
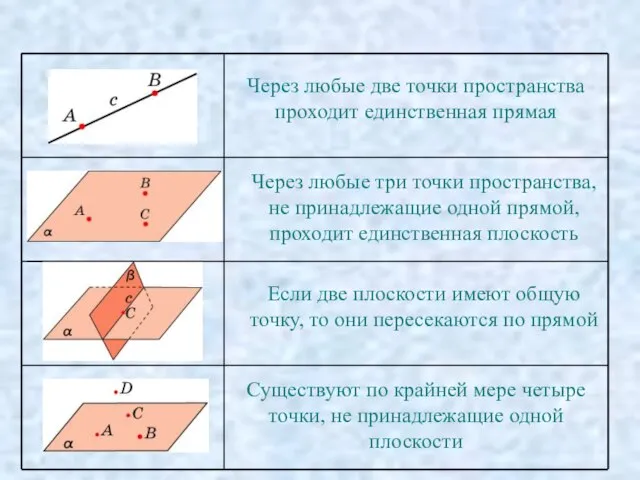
- 2. Через любые две точки пространства проходит единственная прямая Через любые три точки пространства, не принадлежащие одной
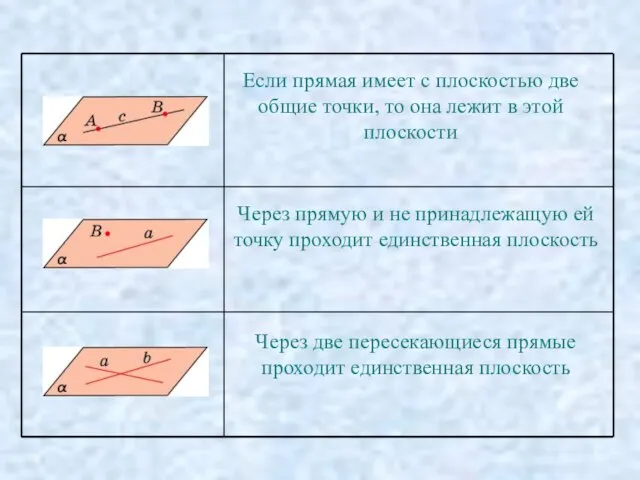
- 3. Если прямая имеет с плоскостью две общие точки, то она лежит в этой плоскости Через прямую
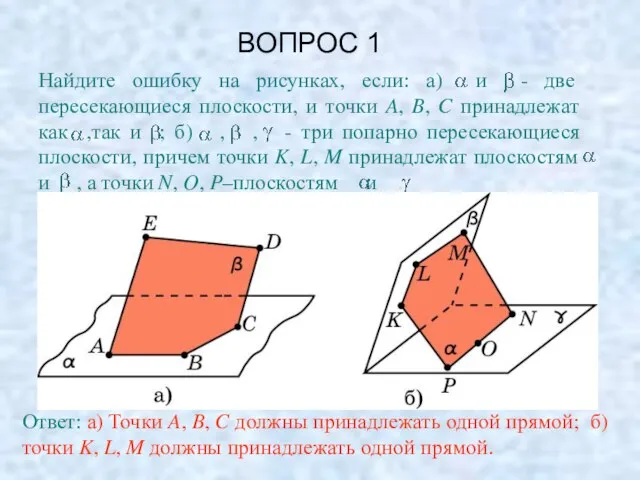
- 4. ВОПРОС 1 Ответ: а) Точки A, B, C должны принадлежать одной прямой; б) точки K, L,
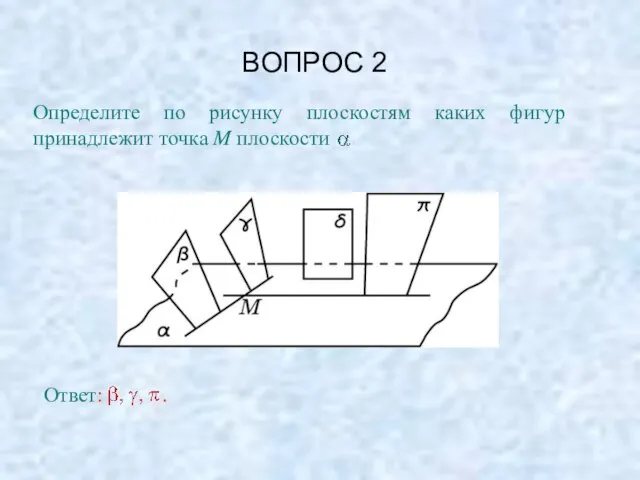
- 5. ВОПРОС 2
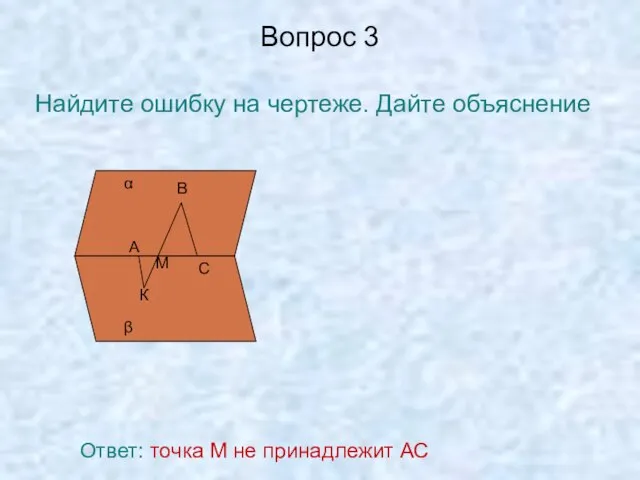
- 6. Вопрос 3 Найдите ошибку на чертеже. Дайте объяснение α β А В С К М Ответ:
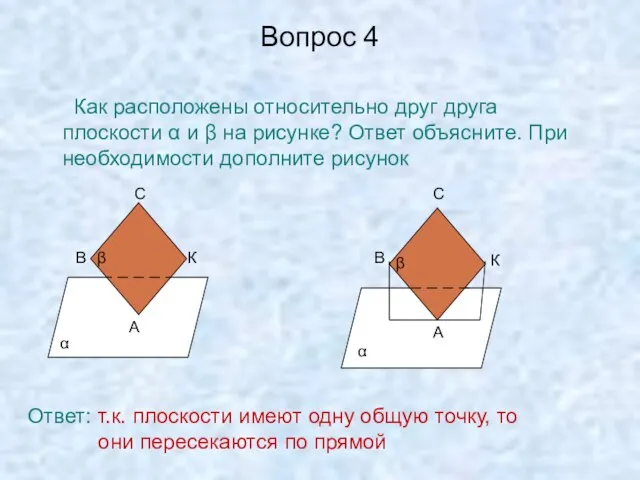
- 7. Вопрос 4 Как расположены относительно друг друга плоскости α и β на рисунке? Ответ объясните. При
- 8. Вопрос 5 Сколько плоскостей можно провести через прямую а? а Ответ: бесконечно много
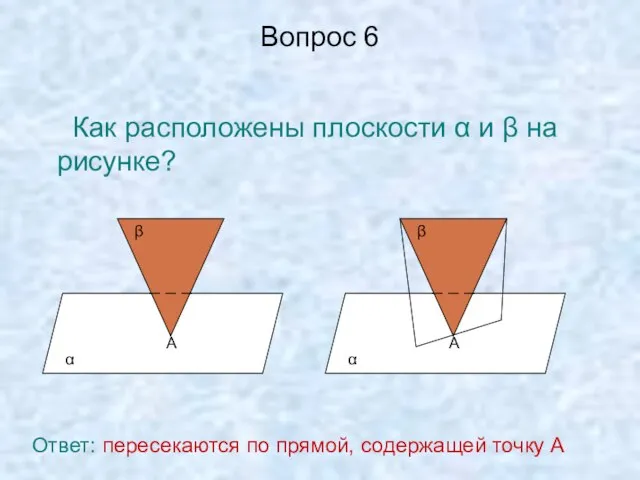
- 9. Вопрос 6 Как расположены плоскости α и β на рисунке? А α β А α β
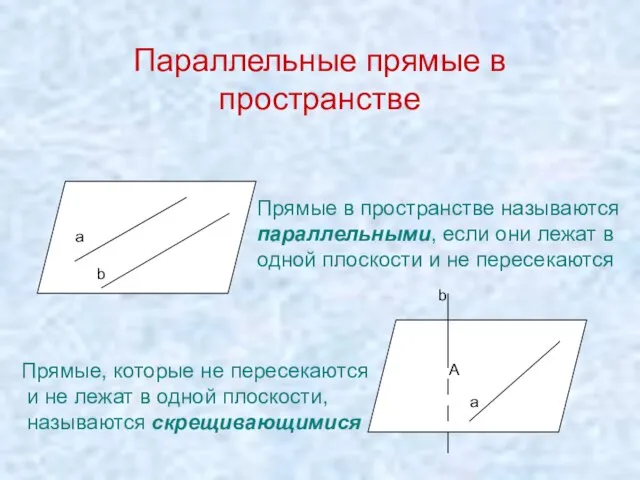
- 10. Параллельные прямые в пространстве А а а b b Прямые в пространстве называются параллельными, если они
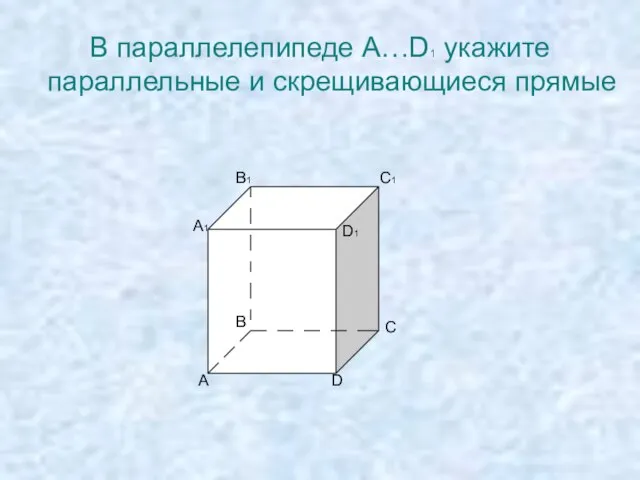
- 11. В параллелепипеде A…D1 укажите параллельные и скрещивающиеся прямые A A1 B B1 C C1 D D1
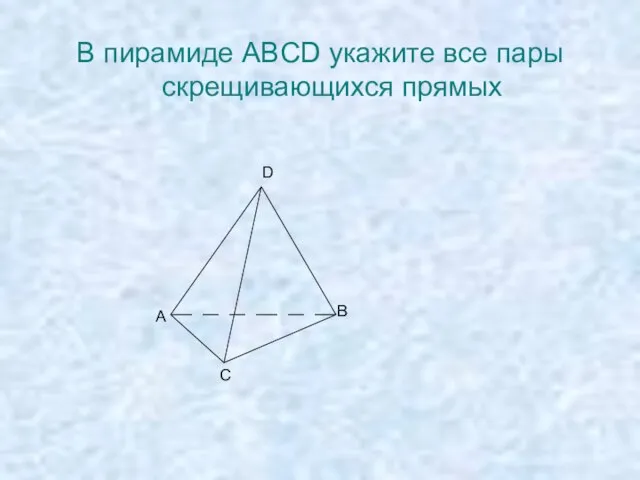
- 12. В пирамиде ABCD укажите все пары скрещивающихся прямых А В С D
- 14. Скачать презентацию

 Планиметрия - презентация по Геометрии_
Планиметрия - презентация по Геометрии_ Решение комбинированных задач с помощью графов
Решение комбинированных задач с помощью графов Фракталы – геометрия природы
Фракталы – геометрия природы Решение задач. Теорема о трех перпендикулярах.
Решение задач. Теорема о трех перпендикулярах. Признаки равенства треугольников 7 класс
Признаки равенства треугольников 7 класс Шар
Шар Многообразие многоугольников
Многообразие многоугольников Знакомство с миром геометрии
Знакомство с миром геометрии Площадь многоугольника 8 класс
Площадь многоугольника 8 класс Графы и их применение
Графы и их применение Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны
Курсовая работа слушателя курсов «Информационно - коммуникационное сопровождение обучения математике» Савицкой Галины Ивановны Развёртка куба
Развёртка куба Двугранный угол. Признак перпендикулярности двух плоскостей
Двугранный угол. Признак перпендикулярности двух плоскостей Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Полезные теоремы, следствия и задачи.
Полезные теоремы, следствия и задачи. Объём призмы
Объём призмы Геометрические построения на плоскости
Геометрические построения на плоскости Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________
Прямоугольный треугольник 8 класс - презентация по Геометрии___________________________________________________________________________________________________________________ Объем конуса
Объем конуса Геометрия Лобачевского
Геометрия Лобачевского Геометрия в архитектуре
Геометрия в архитектуре Золотое сечение в геометрии - презентация по Геометрии_
Золотое сечение в геометрии - презентация по Геометрии_ Урок повторения в 6 классе
Урок повторения в 6 классе Многогранники и кристаллы
Многогранники и кристаллы Симметрия. Осевая и центральная симметрии
Симметрия. Осевая и центральная симметрии Площадь треугольника. Полезные теоремы, следствия и задачи
Площадь треугольника. Полезные теоремы, следствия и задачи Осевая симметрия (6 класс)
Осевая симметрия (6 класс) Основные формулы тригонометрии
Основные формулы тригонометрии