Содержание
- 2. Цели урока: Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами. Научиться находить угол
- 3. Повторение. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? Две прямые
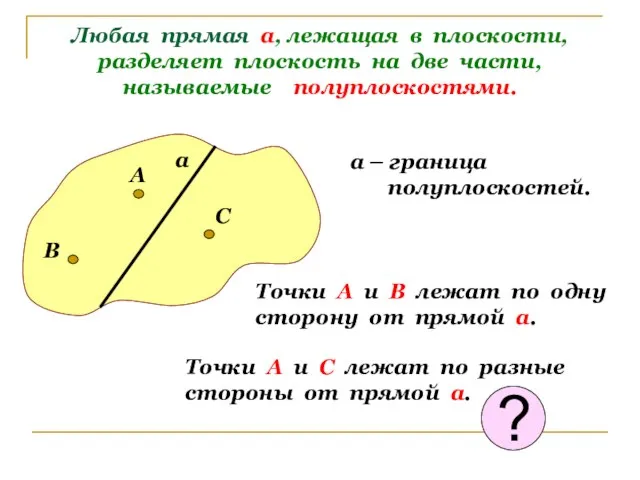
- 4. Любая прямая а, лежащая в плоскости, разделяет плоскость на две части, называемые полуплоскостями. а а –
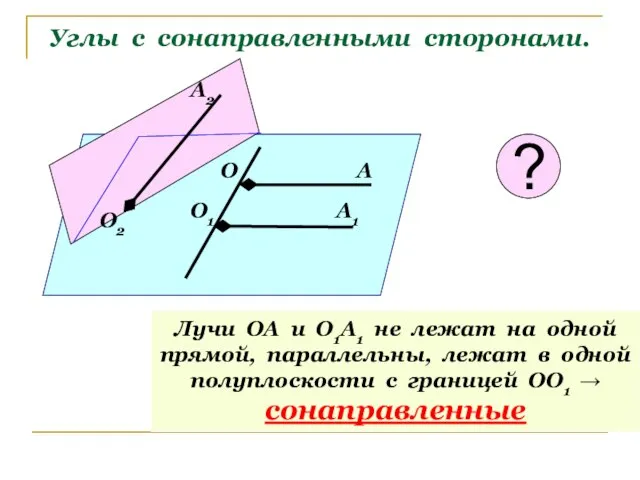
- 5. Углы с сонаправленными сторонами. О А О1 А1 Лучи ОА и О1А1 не лежат на одной
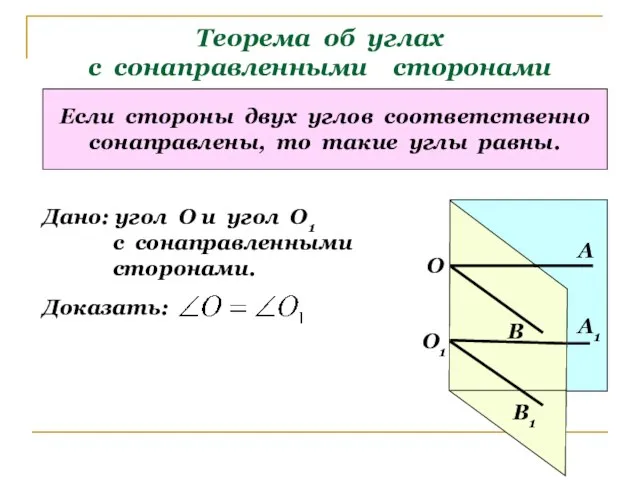
- 6. Теорема об углах с сонаправленными сторонами Если стороны двух углов соответственно сонаправлены, то такие углы равны.
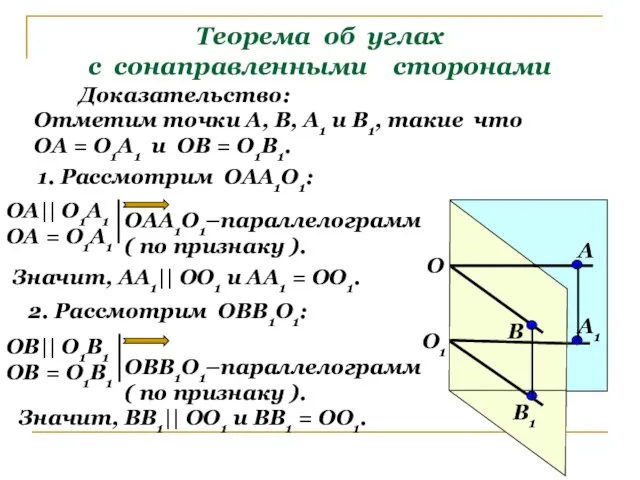
- 7. Теорема об углах с сонаправленными сторонами О1 О А1 В1 В А Доказательство: Отметим точки А,
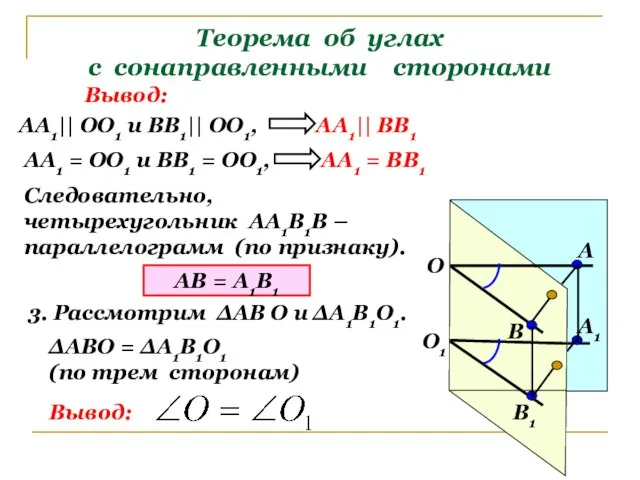
- 8. Теорема об углах с сонаправленными сторонами О1 О А1 В1 В А Вывод: АА1|| ОО1 и
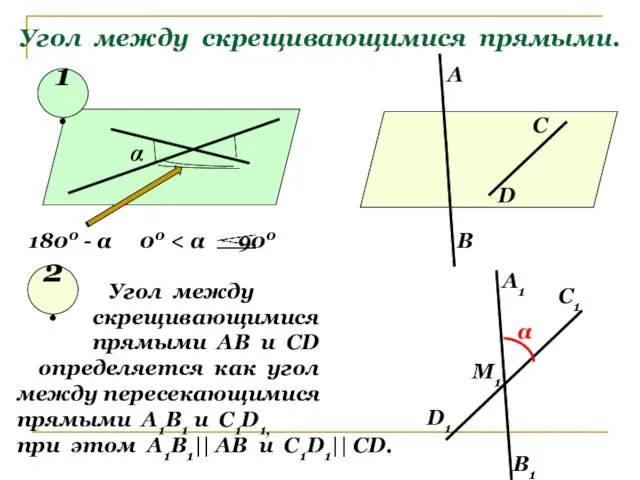
- 9. Угол между скрещивающимися прямыми. α 1800 - α 00 1. 2. Угол между скрещивающимися прямыми АВ
- 10. Практическое задание. Выбрать любую точку М2. Построить А2В2|| АВ и С2D2|| CD. Ответить на вопросы: 1.
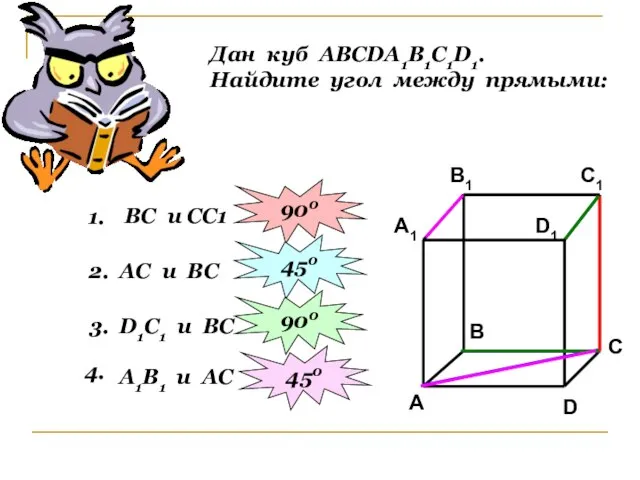
- 11. Дан куб АВСDА1В1С1D1. Найдите угол между прямыми: 1. ВС и СС1 2. 900 АС и ВС
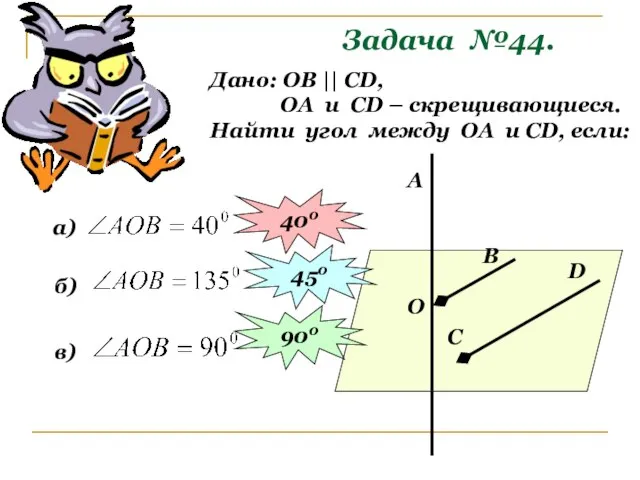
- 12. Задача №44. Дано: ОВ || СD, ОА и СD – скрещивающиеся. Найти угол между ОА и
- 14. Скачать презентацию



 В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Геометрия 7 класс Геометрия 7 класс
Геометрия 7 класс Геометрия 7 класс УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА" Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья
Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья 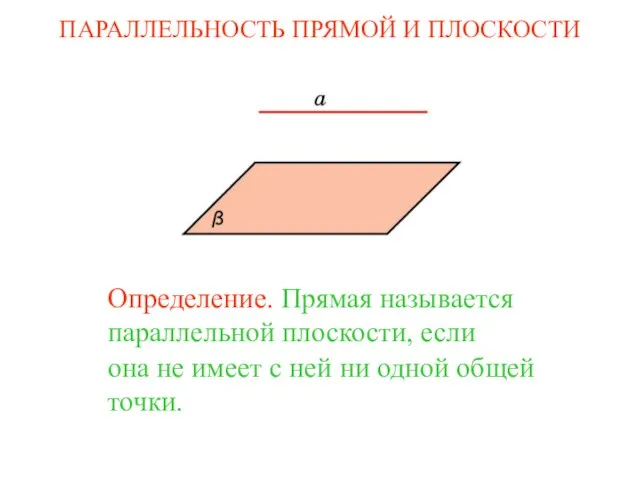 Параллельность прямой и плоскости
Параллельность прямой и плоскости Магические квадраты (5 класс)
Магические квадраты (5 класс) Определение параллельных прямых
Определение параллельных прямых Трехгранный угол
Трехгранный угол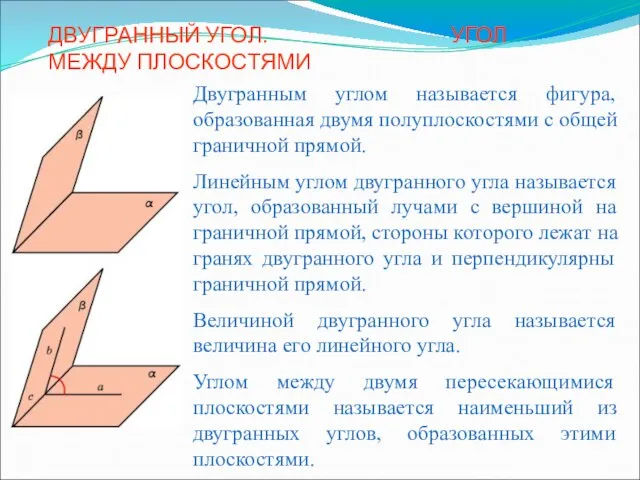 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Прямоугольный параллелепипед
Прямоугольный параллелепипед Правильные выпуклые многогранники
Правильные выпуклые многогранники Геометрические задачи «С2» - презентация по Геометрии_
Геометрические задачи «С2» - презентация по Геометрии_ Параллельные прямые 6 класс
Параллельные прямые 6 класс Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Равнобедренный треугольник
Равнобедренный треугольник Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Нахождение угла между скрещивающимися прямыми
Нахождение угла между скрещивающимися прямыми Объем наклонной призмы, пирамиды и конуса
Объем наклонной призмы, пирамиды и конуса Пирамиды
Пирамиды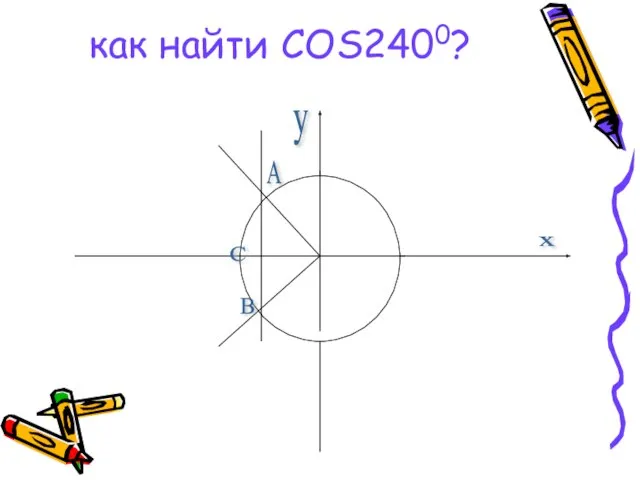 Косинус
Косинус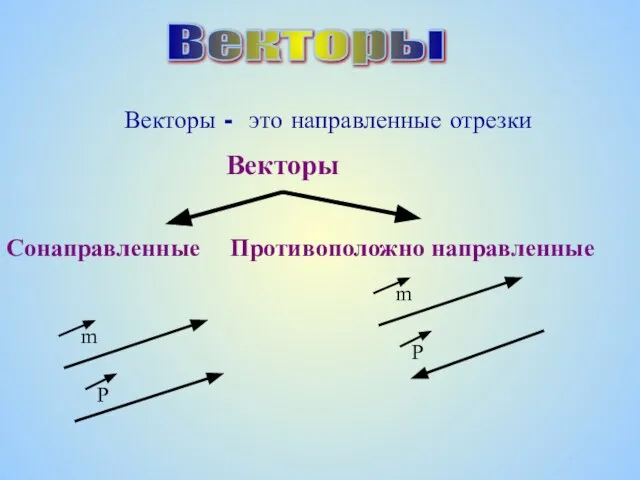 Векторы: Знакомство
Векторы: Знакомство Площадь параллелограмма и треугольника
Площадь параллелограмма и треугольника Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Геометрия 8класс Учитель Бужан Л.В.
Геометрия 8класс Учитель Бужан Л.В. Вычисление площадей фигур в ходе экспериментальной деятельности
Вычисление площадей фигур в ходе экспериментальной деятельности Площадь прямоугольника
Площадь прямоугольника Развитие геометрии
Развитие геометрии Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс)