Содержание
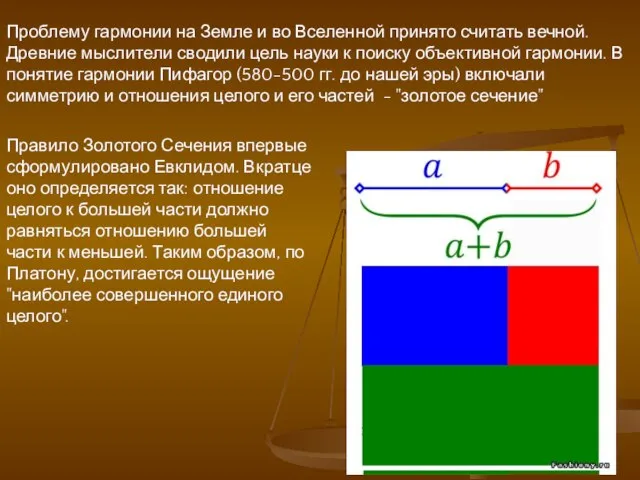
- 2. Правило Золотого Сечения впервые сформулировано Евклидом. Вкратце оно определяется так: отношение целого к большей части должно
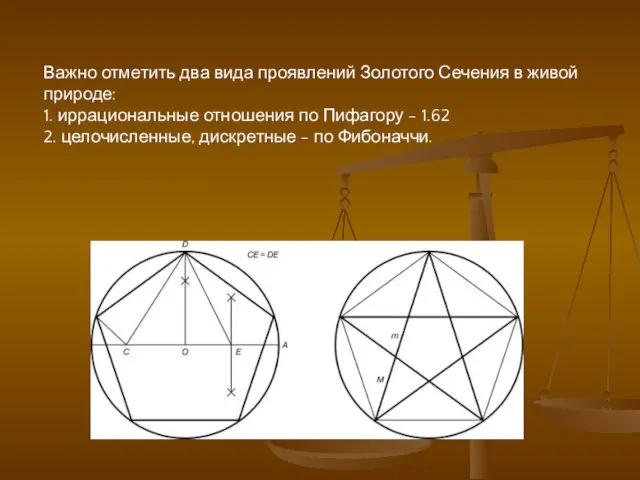
- 3. Важно отметить два вида проявлений Золотого Сечения в живой природе: 1. иррациональные отношения по Пифагору -
- 4. Одна из задач Фибоначчи гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя
- 5. Пифагор был первым, кто обратил внимание на особое «гармоничное» деление любого отрезка, позднее названное «золотым сечением».
- 6. Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают
- 7. Изучая конструкции раковин, ученые обратили внимание на то, что форма раковин поражает своим совершенством и экономичностью
- 8. Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не
- 9. Портрет Моны Лизы (Джоконда) привлекает тем, что композиция рисунка построена на "золотых треугольниках». Таким образом, Леонардо
- 10. Интересные сведения о периодах жизни человека, связанные с числами Фибоначчи. Критические возрасты мужчин соответствуют следующим годам:
- 11. В фотографии используется упрощенный вариант построения «Золотого сечения» или правило «Трети». Заключается оно в следующем: мы
- 12. Знаменитый русский архитектор М.Ф.Казаков широко использовал в своем творчестве золотое сечение. Его талант был многогранным, но
- 13. С помощью правильных пропорций можно получать гармоничные образы, скорректировать недостатки фигуры, а это важно в профессии
- 15. Скачать презентацию










 Смежные и вертикальные углы
Смежные и вертикальные углы Теорема Пифагора задачи
Теорема Пифагора задачи Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1
ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ Петрова Людмила Анатольевна, учитель математики, г.Санкт-Петербург, лицей № 1 Определение и признак перпендикулярности плоскостей
Определение и признак перпендикулярности плоскостей Прямоугольный параллелепипед
Прямоугольный параллелепипед Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса
Медиана. Биссектриса. Высота. «Элементы треугольника» Выполнил работу ученик 10 класса 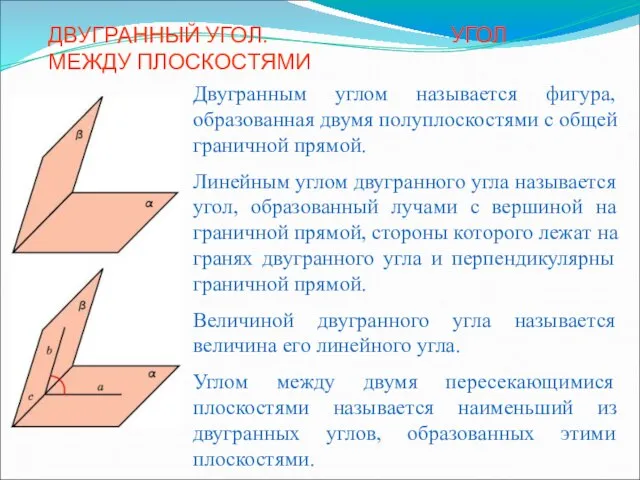 Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Вычисление площадей геометрических фигур
Вычисление площадей геометрических фигур Развёртка куба
Развёртка куба Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Применение параллелограмма
Применение параллелограмма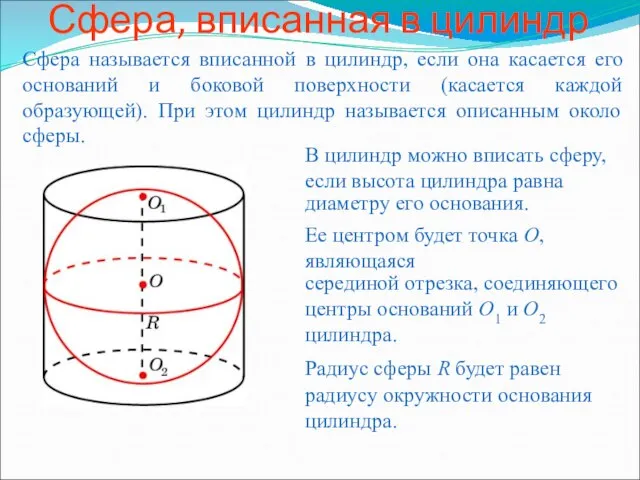 Сфера, вписанная в цилиндр
Сфера, вписанная в цилиндр Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника 8 класс - презентация________________________________________________________________________________ Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Медиана, биссектриса и высота треугольника
Медиана, биссектриса и высота треугольника Музей истории четырёхугольников
Музей истории четырёхугольников Гипотеза пуанкаре и терстона
Гипотеза пуанкаре и терстона Пирамиды
Пирамиды Лабораторный практикум по геометрии 7 класс
Лабораторный практикум по геометрии 7 класс Прямоугольный параллелепипед (5 класс)
Прямоугольный параллелепипед (5 класс) Путешествие в страну Геометрия
Путешествие в страну Геометрия Решение задач на нахождение периметра и площади
Решение задач на нахождение периметра и площади Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Объём пирамиды
Объём пирамиды Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Классическое определение вероятности. Комбинаторные методы решения задач
Классическое определение вероятности. Комбинаторные методы решения задач Луч и угол (7 класс)
Луч и угол (7 класс)