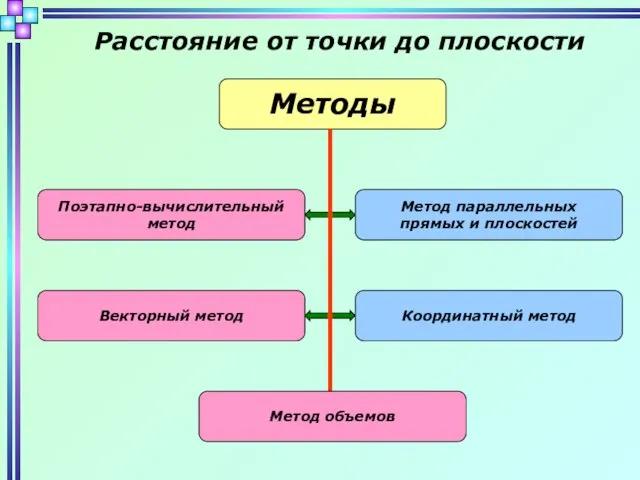
Методы решения геометрических задач ЕГЭ, задание С2 (Расстояние от точки до плоскости)

Расстояние от точки до плоскости
Методы
Поэтапно-вычислительный
метод
Метод параллельных
прямых и плоскостей
Векторный метод
Координатный метод
Метод объемов

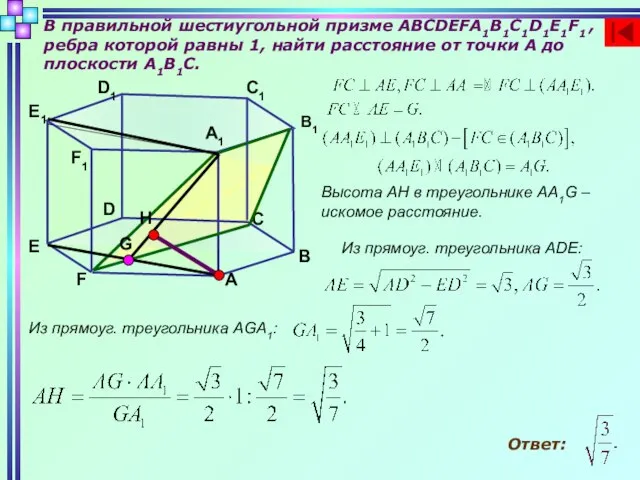
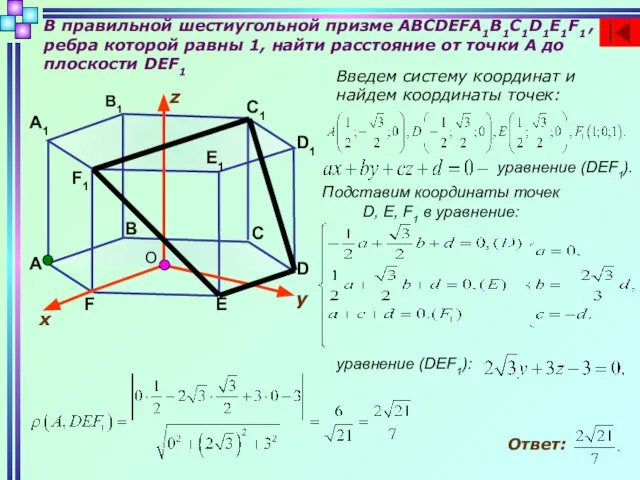
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости А1В1С.
B
C
D
A
C1
D1
E1
F1
A1
B1
E
F
G
H
Высота АН в треугольнике АА1G – искомое расстояние.
Из прямоуг. треугольника ADE:
Из прямоуг. треугольника AGA1:
Ответ:

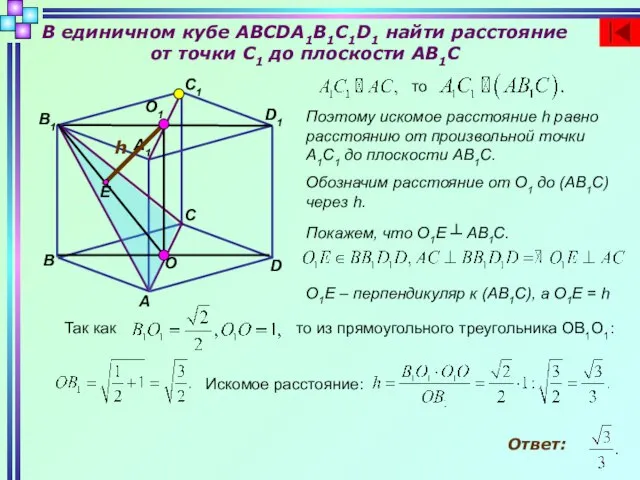
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки C1 до плоскости AB1C
B
D
C
A
A1
B1
C1
D1
то
Поэтому искомое расстояние h равно расстоянию от произвольной точки А1С1 до плоскости АВ1С.
Е
О
О1
h
Обозначим расстояние от О1 до (АВ1С) через h.
Покажем, что О1Е ┴ АВ1С.
О1Е – перпендикуляр к (АВ1С), а О1Е = h
Так как
то из прямоугольного треугольника ОВ1О1:
Искомое расстояние:
Ответ:

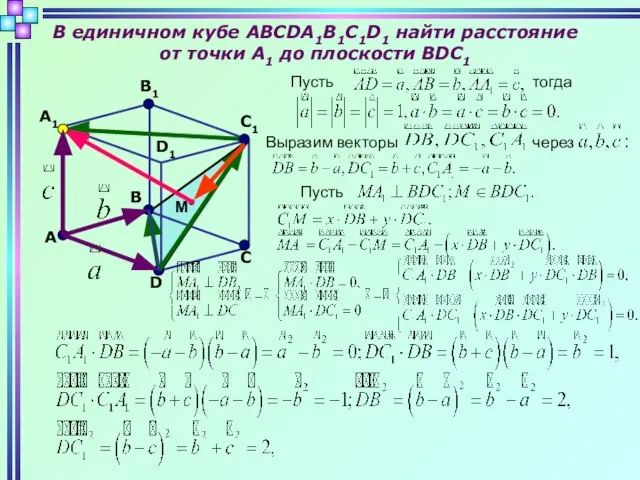
В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1
D
C
B
A
A1
B1
D1
M
C1
Пусть
тогда
Выразим векторы
через
Пусть

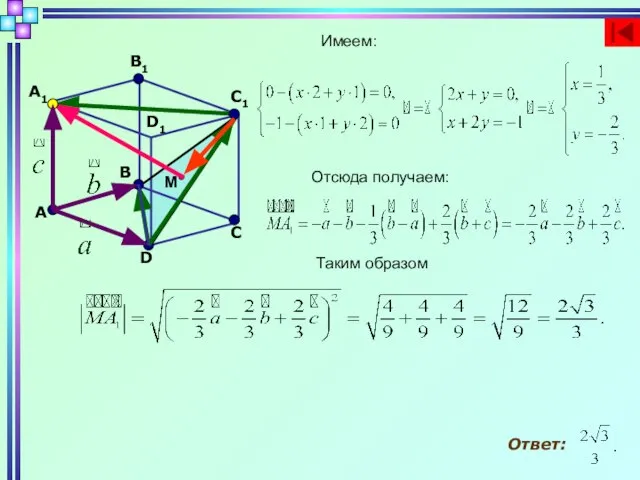
D
C
B
A
A1
B1
D1
M
C1
Имеем:
Отсюда получаем:
Таким образом
Ответ:

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точки А до плоскости DEF1
B
C
D
A
C1
D1
E1
F1
A1
B1
E
F
O
z
y
x
Введем систему координат и найдем координаты точек:
уравнение (DEF1).
Подставим координаты точек D, E, F1 в уравнение:
уравнение (DEF1):
Ответ: